[数据结构与算法]操作系统第三章：银行家算法

银行家算法

银行家算法是最有代表性的避免死锁的算法。
由于该算法能用于银行系统现金贷款的发放而得名的。

1. 银行家算法中的数据结构

设系统中有m类资源，n个进程
（1）可利用资源向量Available。含有m个元素的一维数组，每个元素代表一类可利用的资源数目。
如果Available[j]=k,表示系统中现有Rj类资源k个。

（2）最大需求矩阵Max， 是一个n*m的矩阵，定义了系统中n个进程中的每一个进程对m类资源的最大需求。
如果Max[i,j]=k,则表示进程i，需要Rj类资源的最大数目为k。

（3）分配矩阵Allocation。为n*m的矩阵，它定义了系统中每类资源当前已分配给每个进程的资源数。

Allocation[i,j]=K,表示进程i当前已分得Rj类资源的数目为K。

（4）需求矩阵Need。为n*m的矩阵，表示每个进程尚需的各类资源数。

Need[i,j]=K, 表示进程i还需要Rj类资源K个，方能完成其任务。

?

三个矩阵间的关系：Need[i,j]=Max[i,j]-Allocation[i,j]

2. 银行家算法的处理步骤

设Requesti[j]=k,表示进程Pi需要k个Rj类型的资源
（1）如果Requesti[j]<= Need[i,j],便转向步骤2；否则认为出错，因为它所请求的资源数已超过它所需要的最大值。
（2）如果Requesti[j]<= Available[j],便转向步骤3；否则，表示尚无足够资源，Pi需等待。
（3）系统试探着把资源分配给进程Pi ，并修改下面数据结构中数值
Available[j]:= Available[j]- Requesti[j];
Allocation[i,j]:=Allocation[i,j]+Requesti[j];
Need[i,j]:=Need[i,j]-Requesti[j];

（4）系统执行安全性算法，检查此次资源分配后系统是否处于安全状态以决定是否完成本次分配。若安全，则正式分配资源给进程Pi；否则，不分配资源，让进程Pi等待。

3. 安全性算法

（1）设置两个向量：

• 工作向量work：表示系统可提供给进程继续运行所需的各类资源数目，含有m个元素的一维数组，初始时，work:=Available;

• Finish: 含n个元素的一维数组，表示系统是否有足够的资源分配给n个进程，使之运行完成。

  开始时先令Finish[i]:=false (i=1…n);

  当有足够资源分配给进程i时，再令Finish[i]:=true。

?

（2）从进程集合中找到一个能满足下述条件的进程：Finish[i]=false;Need[i,j]<=work[j]; 若找到，执行步骤（3），否则执行步骤（4）。

?

（3）当进程Pi获得资源后，可顺利执行，直至完成，并释放出分配给它的资源，故应执行：
work[j]:= work[j]+ Allocation[i,j] ;
Finish[i]:=true;
goto step （2）;

?

（4）如果所有进程的Finish[i]=true都满足，则表示系统处于安全状态；否则，系统处于不安全状态。

4.举例

假定系统中有五个进程{P0,P1,P2,P3,P4}和三类资源{A,B,C}，各种资源的数量分别为10、5、7。系统中T0时刻的资源分配情况：

(1) 判断T0时刻的安全性（根据3.6.3.2 安全性算法）

1、初始时：work=Available=【3，3，2】，finish=false。
2、进程集合中找到一个能够满足下列条件的进程：Finish[i]=false，need[i，j]<=work
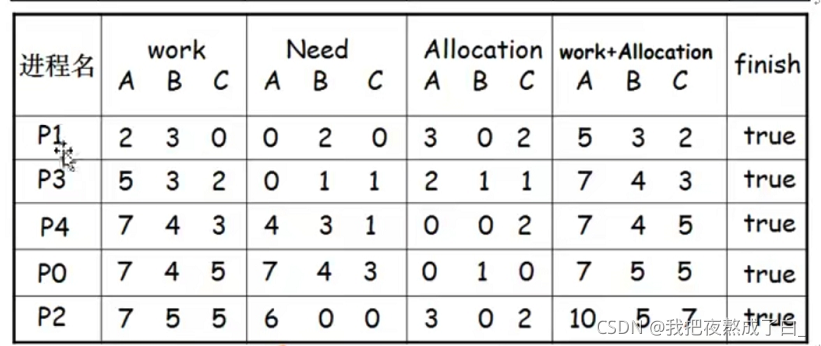
（1）则P1，P3满足，设让P1先执行，从【3，3，2】中拿出【1，2，2】分配给P1，那么P1就可以执行了，执行完以后，释放资源，则work=【2，0，0】+【3，3，2】=【5，3，2】，且finish[1]=true.

（2）从P0、P2、P3、P4 中找满足 finish=false，并need<=work=【5，3，2】，所以P3，P4满足，设让p3执行，则从【5，3，2】中拿出【0，1，1】给P3就可以，那么P3就可以顺利执行完，执行完以后.Finish[3]=true，且work=【5，3，2】+【2，1，1】=【7，4，3】。
重复以上过程

因为所有进程的finish=true，说明系统是处于安全状态的.
存在一个安全执行推进的进程序列{P1-P3-P4-PO-P2}所以系统在T0时候是安全的。

(2) T0时刻时，P1请求资源发出请求向量Requset1(1,0,2)，系统能否分配给它？

利用3.6.3.3 银行家算法的处理步骤：
① Requset1 (1,0,2) <=Need1 (1,2,2)
② Requset1 (1,0,2) <=Available(3,3,2)
③ 试探分配，修改相关值
Avaliable= (3,3,2)-(1,0,2)=(2,3,0)
Allocation1=(2,0,0)+(1,0,2)=(3,0,2)
Need1=(1,2,2)-(1,0,2)=(0,2,0)
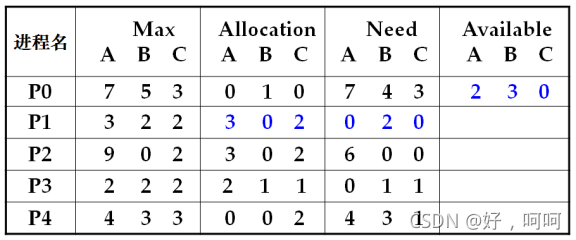
则资源变化为如下表。

④ 再利用3.6.3.2 安全性算法检查此时系统是否安全。

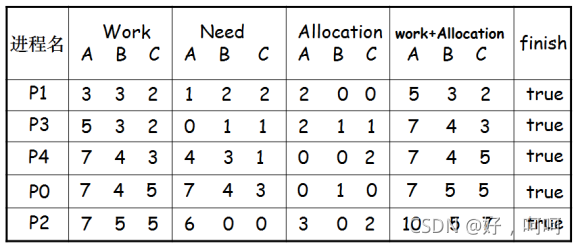
存在安全队列{P1,P3,P4,P0,P2}，所以该时刻安全，可以立即将P1所申请的资源分配给它。

(3) 此时，P4请求资源发出请求向量Requset4(3,3,0)，系统能否分配给它？

利用银行家算法：
① Requset4 (3,3,0) <=Need4 (4,3,1)
② Requset4(3,3,0)>Available(2,3,0)
此时P4等待。

(4) 此时，P0请求资源发出请求向量Requset0(0,2,0)，系统能否分配给它？

利用银行家算法：
① Requset0(0,2,0)<=Need0 (7,4,3)
② Requset0(0,2,0)<=Available(2,3,0)
③ 试探分配，修改相关值
Avaliable= (2,3,0)-(0,2,0)=(2,1,0)
Allocation0=(0,1,0)+(0,2,0)=(0,3,0)
Need0=(7,4,3)-(0,2,0)=(7,2,3)
④ 再利用安全性算法检查此时系统是否安全。很容易看出，可用资源Available(2,1,0)已无法满足任一进程的需求，试探作废，不分给P0资源，P0等待。

5.银行家算法总结

• (1) 首先判断当前时刻的安全性；(安全性算法)

• (2) 若安全，当某进程提出资源申请Requesti时，尝试进行预分配(两个比较，并修改相关值)；

• (3) 判断预分配后的安全性；(安全性算法)

• (4) 若仍安全，则实施预分配；否则，该进程等待。