智能优化算法:类电磁机制算法
摘要:2003 年,Birbil 和 Fang 由于受到电磁场带电粒子间的吸引-排斥机制的启示而提出了基于种群的一种新的随机启发式全局优化算法,即类电磁机制算法(electromagnetism-like machanism algorithm,EM)。算法成功地吸取了传统优化方法以及随机优化方法的优点:简单的寻优原理、需要较少的资源和较快的收敛速度,已经成功地应用于求解无约束优化问题中。
1.算法原理
类电磁机制算法的过程:首先产生初始种群,即随机地在可行域内产生一组初始解,然后根据电磁场里的带电微粒之间的吸引-排斥的机制原理,把每一个可行域中的粒子都看成一个个带电粒子。这些带电粒子的电荷量是由目标函数的函数值来确定的,电荷量决定了带电粒子受到的排斥力或者吸引力的大小,即粒子具有越优的目标函数值,则该粒子就具有越强的吸引力。通过计算当前粒子所受到其它粒子所施加给其的合力,EM 算法以此来决定当前粒子下一步的移动方向。最后根据预先规定的更新规则来产生下一代粒子。所有粒子都完成了上述操作后,可行域中所有粒子的位置都被更新了一次,EM 算法这时候就完成了一轮迭代过程。若未满足算法结束条件,则返回到局部搜索步骤进行下一次迭代。直至所有粒子最终都收敛到某一极小的邻域,并满足一定的终止条件后,优化问题就得到了最优解。
1.1 初始化
从可行域中均匀地随机产生 N N N个点 { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN}作为初始种群. 其中 x i = ( x 1 i , x 2 i , . . , x n i ) , i = 1 , 2 , . . . , N x^i=(x_1^i,x_2^i,..,x_n^i),i=1,2,...,N xi=(x1i?,x2i?,..,xni?),i=1,2,...,N,n 为问题的维数. 然后计算每个粒子的目标函数 f ( x i ) f(x^i) f(xi)?,并将函数值最优的粒子记为 x b e s t x^{best} xbest?。
1.2 局部搜索
? 局部搜索用于更新当前一个粒子. 通过在一定范围内搜索比该粒子更优的粒子,并使得该粒子朝更精确
的解移动,达到局部更新的效果. 可对所有粒子进行局部搜索,也可只对当前最优粒子进行局部搜索. 将局部
搜索完后的最优粒子仍然记为
x
b
e
s
t
x^{best}
xbest?.
1.3 电荷量及力的计算
由 Birbil 和 Fang 构造的粒子的电荷量的计算为:
q
i
=
e
x
p
(
?
n
(
f
(
x
i
)
?
f
(
x
b
e
s
t
)
)
/
∑
k
=
1
N
(
f
(
x
k
)
?
f
(
x
b
e
s
t
)
)
)
,
i
=
1
,
2
,
.
.
,
N
(1)
q^i=exp(-n(f(x^i)-f(x^{best}))/\sum_{k=1}^N(f(x^k)-f(x^{best}))),i=1,2,..,N \tag{1}
qi=exp(?n(f(xi)?f(xbest))/k=1∑N?(f(xk)?f(xbest))),i=1,2,..,N(1)
显然,目标函数值越小(即越优)的粒子所带电荷量越大。
然后仿照电磁场中力的计算公式,计算每个粒子受到另一个粒子的作用力,再根据叠加原理,计算粒子所受到的合力. 设
F
i
j
F^{ij}
Fij表示粒子
i
i
i受到粒子
j
j
j的作用力,
F
i
F_i
Fi? 表示粒子
i
i
i?所受到的合力,则
F
i
j
=
{
(
x
j
?
x
i
)
q
i
q
j
∣
∣
x
j
?
x
i
∣
∣
2
,
f
(
x
j
)
<
f
(
x
i
)
(
x
i
?
x
j
)
q
i
q
j
∣
∣
x
j
?
x
i
∣
∣
2
,
f
(
x
j
)
<
f
(
x
i
)
(2)
F^{ij}=\begin{cases} (x^j-x^i)\frac{q^iq^j}{||x^j-x^i||^2},f(x^j)<f(x^i)\\ (x^i-x^j)\frac{q^iq^j}{||x^j-x^i||^2},f(x^j)<f(x^i) \end{cases}\tag{2}
Fij={(xj?xi)∣∣xj?xi∣∣2qiqj?,f(xj)<f(xi)(xi?xj)∣∣xj?xi∣∣2qiqj?,f(xj)<f(xi)?(2)
F i = ∑ j ≠ i N F i j , i , j = 1 , 2 , . . . , N (3) F^i=\sum_{j\neq i}^NF^{ij},i,j=1,2,...,N\tag{3} Fi=j?=i∑N?Fij,i,j=1,2,...,N(3)
由式(3)可知,粒子的受力方向是由粒子的优劣来确定的。即目标函数值较优的粒子吸引目标函数值较差的
粒子,目标函数值较差的粒子排斥目标函数值较优的粒子。
1.4 移动粒子
按照式(4)计算完合力后,粒子将沿着合力的方向移动,新的位置如下:
x
i
=
x
i
+
λ
(
F
i
/
∣
∣
F
i
∣
∣
)
R
N
G
,
i
=
1
,
2
,
.
.
.
,
N
(5)
x^i=x^i+\lambda(F^i/||F^i||)R_{NG},i=1,2,...,N \tag{5}
xi=xi+λ(Fi/∣∣Fi∣∣)RNG?,i=1,2,...,N(5)
式中,
λ
∈
(
0
,
1
)
λ ∈(0,1)
λ∈(0,1) 为随机数. 移动过程中,其可行移动范围由
R
N
G
R_{NG}
RNG?? 给出,
R
N
G
=
(
v
1
,
v
2
,
…
,
v
n
)
R_{NG} =(v_1 ,v_2 ,…,v_n )
RNG?=(v1?,v2?,…,vn?),表示向上边界
u
k
u_k
uk?和下边界
l
k
l_k
lk??? 移动的可行步长。 且有
v
k
=
{
u
k
?
x
k
i
,
F
k
i
>
0
x
k
i
?
l
k
,
e
l
s
e
(6)
v_k=\begin{cases} u_k-x_k^i,F_k^i>0\\ x_k^i-l_k,else \end{cases}\tag{6}
vk?={uk??xki?,Fki?>0xki??lk?,else?(6)
其中,
F
k
i
F_k^i
Fki? 为第
i
i
i个粒子的合力的第
k
k
k?个分量。
经过以上 4 个步骤,完成了 EM 算法的一次迭代,粒子的位置也得到了更新。
算法步骤
步骤1:初始化粒子种群。
步骤2:计算适应度值,并记录最优位置。
步骤3:进行局部搜索。
步骤4:计算电荷量和力,并更新粒子位置。
步骤5:计算适应度值,并更新最优位置。
步骤6:判断是否达到最大迭代次数,如果达到则输出最优结果,否则重复步骤3-6。
2.算法结果
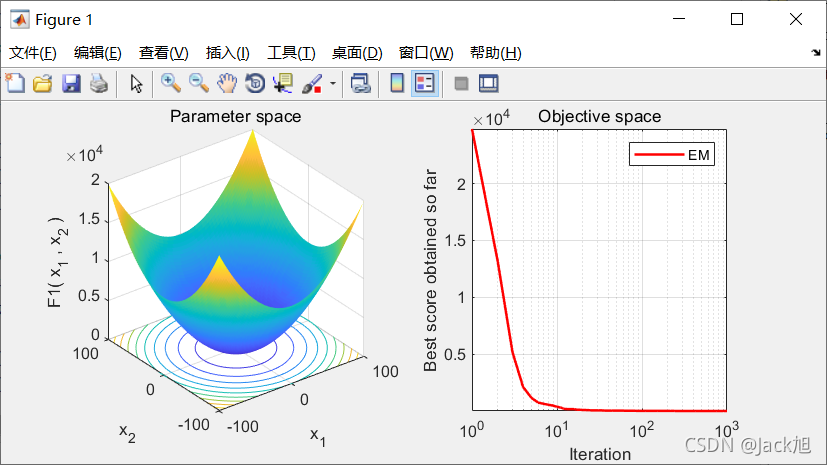
3.参考文献
[1]刘梦楠. 类电磁机制算法的研究与改进[D].西安电子科技大学,2014.
[1]周斌,陈晶,张雅雯,薛东.一种类电磁机制算法在锅炉主汽温系统的研究[J].安徽水利水电职业技术学院学报,2020,20(01):16-19.