[数据结构与算法]堆

堆

我们一般所说的堆，指的是二叉堆，数据结构（严蔚敏）是这样定义的。

除二叉堆以外也有很多种类的堆，d堆，左氏堆，斜堆等
我们可用一个数组来表示二叉堆

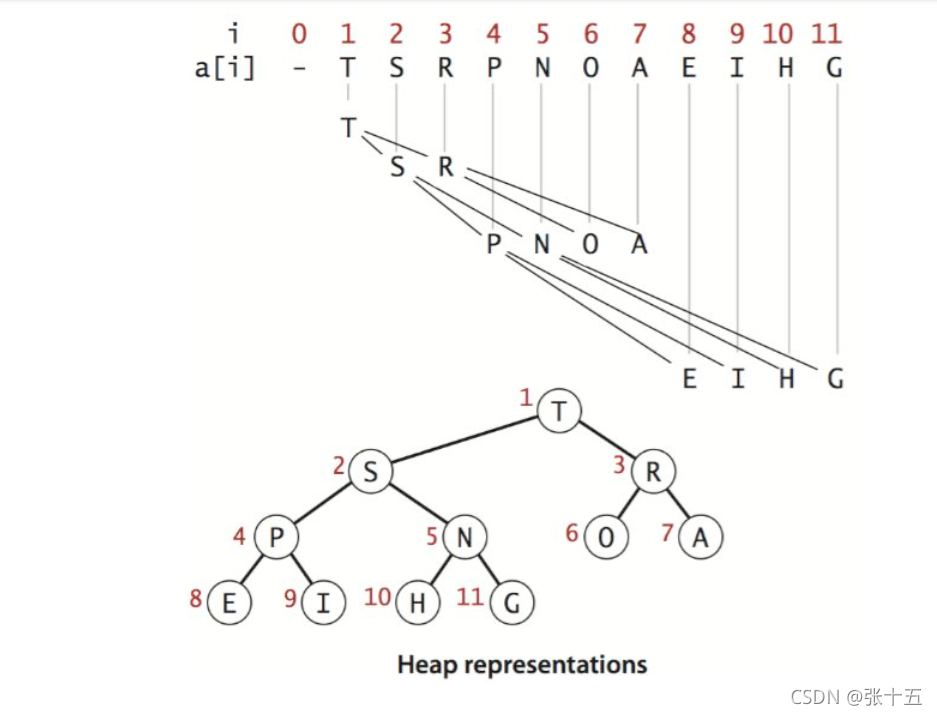
很显然的完全二叉树

优先队列（priority_queue）

什么是优先队列呢?在优先队列中，元素被赋予优先级，当访问元素时，具有最高级优先级的元素先被访问。即优先队列具有最高级先出的行为特征。它可以说是队列和排序的完美结合体，不仅可以存储数据，还可以将这些数据按照我们设定的规则进行排序。

我们可以结合二叉堆与队列的思想，用一个数组（队列）来实现一个优先队列。

优先队列是至少允许下列两种操作的数据结构: insert（插入)，它的工作是显而易见的;delete(删除最小项)，它的工作是找出、返回和删除优先队列中最高优先级的元素。insert操作等价于Push_Queue (入队)，而delete则是队列操作Pop_Queue（出队）在优先队列中的等价操作。

我在此实现的小根堆，元素越小，优先级越高

#define INITSIZE 20  //初始化的大小
#define EXPANDTIMES 2 //每次的扩容倍数
typedef int ELemType; //用int来模拟数据项类型

typedef struct
{
	ELemType* data; //存储数据的初始位置
	int capacity; //容量（总共的:未使用的+已经使用的）
	int size;//已经使用的
}Priority_Queue;

初始化

bool Init_Priority_Queue(Priority_Queue* PQ)
{
	assert(PQ != NULL);//对输入也检测一下，使用空指针可能会导致程序奔溃，具体原因自己去搜，后续不解释
	PQ->data = (ELemType*)malloc(sizeof(ELemType) * INITSIZE);//申请一段堆空间来存储元素
	//assert(PQ->data != NULL);//因为malloc可能会申请失败，判断一下
	if (PQ->data == NULL)
	{
		return false;
	}
	else
	{
		PQ->capacity = INITSIZE;//初始容量通过宏定义设定
		PQ->size = 0;//初始使用的大小当然是0喽
		return true;
	}
}

修改容量

bool Change_Priority_Queue(Priority_Queue* PQ, int flag)//改变容量
{
	assert(PQ != NULL);
	ELemType* temp = PQ->data;
	int newsize = flag == -1 ? PQ->capacity / EXPANDTIMES : PQ->capacity * EXPANDTIMES;//简单的判断，
	temp = (ELemType*)realloc(temp, newsize * sizeof(ELemType));//扩容也可能会失败，这样做是防止旧数据丢失
	if (temp == NULL)
	{
		return false;
	}
	else
	{
		PQ->data = temp;
		PQ->capacity = newsize;
		return true;
	}
}

判空

bool IsEmpty_Priority_Queue(Priority_Queue* PQ)
{
	assert(PQ != NULL);
	return PQ->size == 0;//只用检测一下使用的大小为不为0，就ok
}

清空

bool Clear_Priority_Queue(Priority_Queue* PQ)
{
	assert(PQ != NULL);
	free(PQ->data);//因为空间是malloc来的，不用就free掉
	Init_Priority_Queue(PQ);//最简单的做法，重新给他初始化下，就消除了数据，也缩小了容量
	//PQ->size = 0;//最最最简单的方法因为数据是否有效，我们说了算，容量没变
	return true;
}

获取堆顶元素

我在此没有使用0号下标（浪费了），当然也可以使用，不过父子节点的下标关系就会有些许改变，

ELemType Get_Priority_Queue(Priority_Queue* PQ)
{
	assert(PQ != NULL);
	if (IsEmpty_Priority_Queue(PQ))
	{
		printf("Priority_Queue is Empty \n");
		return -1;
	}
	else
	{
		return PQ->data[1];
	}
}

插入

插入之前先对大小进行判断，不够的话就先扩容在插入。(0号浪费了，所以capacity先减一。

插入的思想：先将插入的数据放在最后一个位置。

在不断(递归）的判断他与其父节点的大小关系，若新插入的元素优先级高，即将他和他的父亲调换。(Shift_Up_Priority_Queue函数的作用）

bool Insert_Priority_Queue(Priority_Queue* PQ, ELemType e)
{
	assert(PQ != NULL);
	if (PQ->size == PQ->capacity - 1)
	{
		Change_Priority_Queue(PQ, 1);
	}
	PQ->size++;
	PQ->data[PQ->size] = e;
	return Shift_Up_Priority_Queue(PQ, PQ->size);
}

删除

删除之后，调整位置之前，先对大小进行判断，容量过大的话就先缩容在调整位置

删除的思想：将最后一个数据放在第一个位置。

在不断(递归）的判断他与其两个（不一定有）子节点其中最小的大小关系，若其子节点优先级高，即将他和他的子节点调换。（Shift_Down_Priority_Queue函数的作用）

bool Delete_Priority_Queue(Priority_Queue* PQ)
{
	assert(PQ != NULL);
	PQ->data[1] = PQ->data[PQ->size];
	PQ->size--;
	if (PQ->capacity > INITSIZE && PQ->capacity / EXPANDTIMES > PQ->size)
		Change_Priority_Queue(PQ, -1);
	return Shift_Down_Priority_Queue(PQ, 1);
}

向下调整

bool Shift_Down_Priority_Queue(Priority_Queue* PQ, int pos)
{
	assert(PQ != NULL);
	if (pos * 2 > PQ->size)//没有子节点
	{
		
	}
	else if (pos * 2 == PQ->size )//只有一个子节点
	{
		if(PQ->data[pos * 2] < PQ->data[pos])
			{
				ELemType T = PQ->data[pos];
				PQ->data[pos] = PQ->data[pos * 2];
				PQ->data[pos * 2] = T;
			}
	}
	else//有点个子节点
	{
		ELemType MIN = PQ->data[pos * 2] < PQ->data[pos * 2 + 1] ? PQ->data[pos * 2] : PQ->data[pos * 2 + 1];
		int MINPOS = MIN == PQ->data[pos * 2] ? pos * 2 : pos * 2 + 1;//选出子结点中最小的及其小标
		if (MIN < PQ->data[pos])
		{
			ELemType T = PQ->data[pos];
			PQ->data[pos] = MIN;
			PQ->data[MINPOS] = T;
			Shift_Down_Priority_Queue(PQ, MINPOS);
		}
	}
	return true;
}

向上调整

bool Shift_Up_Priority_Queue(Priority_Queue* PQ, int pos)
{
	assert(PQ != NULL);
	if (pos == 1)
	{
		return true;
	}
	else if (PQ->data[pos] >= PQ->data[pos/2])
	{
		return true;
	}
	else
	{
		ELemType T = PQ->data[pos];
		PQ->data[pos] = PQ->data[pos / 2];
		PQ->data[pos / 2] = T;
		return Shift_Up_Priority_Queue(PQ, pos / 2);
	}
}