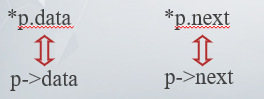2.1约瑟夫环问题
约瑟夫环问题由古罗马史学家约瑟夫(Josephus)提出,他参加并记录了公元66—70年犹太人反抗罗马的起义。在城市沦陷之后,他和40名死硬的将士在附近的一个洞穴中避难。这些起义者表决说“要投降毋宁死”。于是,约瑟夫建议每个人轮流杀死他旁边的人,而这个顺序是由抽签决定的。约瑟夫有预谋地抓到了最后一签,并且,作为洞穴中的两个幸存者之一,他说服了他原先的牺牲品一起投降了罗马。?
?模型抽象:
设 n(n>0)个人围成一个环,n 个人的编号分别为1,2,…,n,从第 1 个人开始报数,报到 m 时停止报数,报 m 的人出环,再从他的下一个人起重新报数,报到 m 时停止报数,报m的人出环,……,如此下去,直到所有人全部出环为止。对于任意给定 n 和 m,求 n 个人出环的次序。
?2.2线性表的逻辑关系(前驱后继)
2.2.1线性表的定义?
线性表:n个具有相同类型的数据元素的有限序列
线性表的长度:线性表中数据元素的个数
空表:长度等于的零的线性表
线性表? L=(a1,a2,....an)
a1称为表头元素
an称为表尾元素
在这个序列中,元素a1无前驱,元素an无后继?
序偶:两个具有固定次序的元素组成的序列,记作(a,b),且称 a 是 b 的前驱,b 是 a 的后继
?2.3线性表的顺序存储结构及实现
2.3.1顺序表的存储结构
顺序表:线性表的顺序存储结构(用一段地址连续的存储单元依次存储线性表的数据元素)
顺序表的属性:
1.存储空间的起始位置
2.顺序表的容量(最大长度)
3.顺序表的当前长度
随机存取:确定了存储顺序表的起始位置,计算任意一个元素的存储地址的时间是相等的?,即在O(1)时间内存取数据元素
存储结构——数据及其逻辑结构在计算机中的表示
存取结构——在一个数据结构上对(按位置)查找操作的时间性能
顺序表是一种随机存取的存储结构,其含义为:在顺序表这种存储结构上进行的(按位置查找操作,其时间性能为O(1)
?2.3.2顺序表的实现
?整体模板
const int MaxSize = 100;
template <typename DataType> //定义模板类SeqList
class SeqList
{
public:
SeqList( ); //建立空的顺序表
SeqList(DataType a[ ], int n); //建立长度为n的顺序表
~SeqList( ); //析构函数
int Length( ); //线性表的长度
DataType Get(int i); //按位查找
int Locate(DataType x ); //按值查找
void Insert(int i, DataType x); //插入操作
DtaType Delete(int i); int Empty( ); //删除操作
int Empty( ); //判断线性表是否为空
void PrintList( ); //遍历操作
private:
DataType data[MaxSize]; //存放数据元素的数组
int length; //线性表的长度
};?1.无参构造函数——初始化顺序表
InitList
??? 输入:无
??? 功能:表的初始化,建一个空表
??? 输出:无
SeqList<DataType> :: SeqList( ) { Length = 0; }2.有参构造函数——建立顺序表
SeqList<DataType> :: SeqList(DataType a[ ], int n) { if (n > MaxSize) throw “参数非法”; for (int i = 0; i < n; i++) data[i] = a[i]; length = n; }
3.析构函数——销毁顺序表
顺序表是静态存储分配,在顺序表变量退出作用域时自动释放该变量所占内存单元,因此无需销毁,析构函数为空。
4.判空操作
int SeqList<DataType> :: Empty( ) { if (length == 0) return 1; else return 0; }只需要判断长度length是否为0
5.求顺序表的长度
int SeqList<DataType> :: Length( ) { return length ; }6.遍历操作
template <typename DataType> void SeqList<DataType> :: PrintList { for (int i = 0; i < n; i++) cout << data[i] << "\t"; cout<<endl; }7.按位查找
template <typename DataType> DataType SeqList<DataType> :: Get(int i) { if (i < 1 && i > length) throw "查找位置非法"; else return data[i - 1];
8.按值查找?
template <typename DataType> int SeqList<DataType> :: Locate(DataType x) { for (int i = 0; i < length; i++) if (data[i] == x) return i+1; //返回其序号i+1 return 0; //退出循环,说明查找失败 }
9.插入操作?
template <typename DataType> void SeqList<DataType> :: Insert(int i, DataType x) { if (length == MaxSize) throw "上溢"; if (i < 1 || i > length + 1) throw "插入位置错误"; for (int j = length; j >= i; j--) data[j] = data[j - 1]; //第j个元素存在数组下标为j-1处 data[i - 1] = x; length++; }?
10.删除操作
?删除算法:
????????必须从第i+1个元素(下标为i)开始,直至将最后一个元素前移为止,并且在移动元素之前要取出被删元素。
DataType SeqList<DataType> ::Delete(int i) { DataType x; if (length == 0)throw "下溢"; if (i <1 || i> length) { x = data[i - 1]; for (int j = 0; j < length; j++) { data[j - 1] = data[j]; } length--; return x; } }?时间复杂度:O(n);
2.4线性表的链接存储结构及实现?
2.4.1单链表的存储结构?
?
?单链表:用一组任意的存储单元(连续、不连续、零散)存放线性表的元素
?单链表通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起,由于每个结点只有一个指针域,故称为单链表。
?
?
?单链表的结点结构定义
template <typename DataType>
struct Node
{
DataType data;
struct Node *next;
} Node;
头指针:指向第一个节点的存储地址
尾标志:终端结点的指针域为空
头结点:在第一个元素结点之前附设一个类型相同的结点

?单链表:
?
设指针 p 指向某个Node类型的结点
该结点用 *p 来表示,*p 为结点变量。将“指针 p 所指结点”简称为“结点 p”
?
2.4.2单链表的实现
1.单链表的实现——初始化
template <typename DataType> LinkList<DataType> :: LinkList( ) { first = new Node<DataType>; //生成头结点 first->next = nullptr; //头结点的指针域置空 }2.判空操作
template <typename DataType> int LinkList<DataType> :: Empty( ) { if (first->next == nullptr) return 1 else return 0; }只需判断单链表是否只有头结点,即判断?first->next 是否为空
3.遍历操作
实现工作指针后移:
?first指向头结点:first的作用是表示单链表的开始,通常不修改头指针。
(first->next=p)
?伪代码:
输入:无 功能:遍历单链表 PrintList 输出:单链表的各个数据元素 1. 工作指针 p 初始化; 2. 重复执行下述操作,直到指针 p 为空: 2.1 输出结点 p 的数据域; 2.2 工作指针 p 后移;template <typename DataType> void LinkList<DataType> :: PrintList( ) { Node<DataType> *p = first->next; //工作指针p初始化 while (p != nullptr) { cout << p->data << "\t"; p = p->next; //工作指针p后移,注意不能写作p++ } cout << endl; }4.单链表的实现——长度
增加计数器
?
int LinkList<DataType> :: Length( ) { Node *p = first->next; int count = 0; while (p != nullptr){ count++; p = p->next; } return count; }5.单链表的实现——按位查找
DataType LinkList<DataType> :: Get(int i) { Node<DataType> *p = first->next; //工作指针p初始化 int count = 0; //累加器count初始化 while (p != nullptr) { count++; if(count == i) break; //查找成功直接退出循环 p = p->next; //工作指针p后移 } if (p == nullptr) throw "查找位置错误"; else return p->data; }?6.单链表的实现——按值查找
int LinkList<DataType> :: Locate(DataType x) { Node<DataType> *p = first->next; //工作指针p初始化 int count = 0; //累加器count初始化 while (p != nullptr) { count++; if (p->data == x) return count; //查找成功,结束函数并返回序号 p = p->next; } return 0; //退出循环表明查找失败 }7.单链表的实现——插入操作?
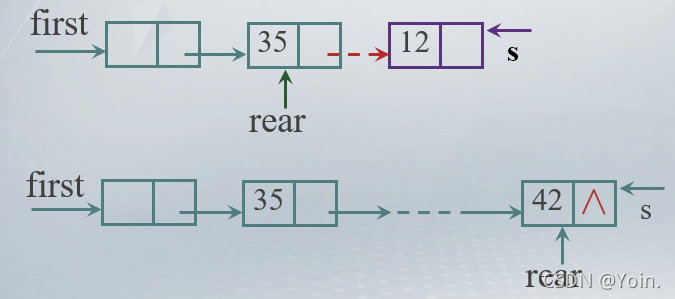
算法描述:
node s = new node(); s->date = x; s->next = p->next; p->next = s;?
不带头指针的插入 :
实现代码:
template <typename DataType> viod LinkList<DataType>::Insert(int i, DataType x) { Node<DataType>* p = first;//工作指针 Node<DataType>* s = new Node<DataType>;//待插入指针 s->date = x; int count = 0;//计数器 while (p!=nullptr) { count++; if (count == i) {//寻找待删除位置 break; } p = p->next; } if(p==nullptr) throw "错误"; else { s->next = p->next; p->next = s;//插入算法 } }8.单链表的实现——删除操作?
注意在表头与表尾删除?:
表头:
表尾:
实现算法:
q = p->next; p-> = q->next; delete q;实现代码:
template <typename DataType> viod LinkList<DataType>::Delete(int i) {//传入待删除位置 Node<DataType>* p = first;//工作指针 Node<DataType>* q = nullptr;//待插入指针 DataType x; int count = 0;//计数器 while (p!=nullptr) { count++; if (count == i-1) {//寻找待删除位置的前一个结点 break; } p = p->next; } if(p==nullptr||p->next == nullptr) throw "错误"; else { q = p->next; x = q->data;//暂存被删除的结点的值 p->next = q->next;//摘链 delete q;//释放空间 return x; } }9.构建单链表
(1)头插法:每次将新申请的节点插在头结点的后面
????????????????first an? an-1? .... a3 a2 a1? 倒序
template <typename DataType> LinkList<DataType>::LinkList(DataType a[],int n) {//传入待插入数组以及待插入元素个数 first = new Node<DataType>; first->next = nullptr;//定义头指针初始化链表 for (int i = 0; i < n; i++) { Node<DataType>* s = nullptr;//待插入结点 s = new Node<DataType>; s->data = a[i];//待插入结点data域赋值 s->next = first->next; first->next = s;//将s插入头结点后部 } }
(2)尾插法:每次将申请的节点插在终端结点的后面
? ? ? ? first a1 a2 a3 ..... an? ?顺序插入
主要思想:插入一个元素,移动一下头指针代替指针(头指针不能随意移动),相当于每次在头指针后部插入
实现代码:
template <typename DataType> LinkList<DataType>::LinkList(DataType a[],int n) {//传入待插入数组以及待插入元素个数 first = new Node<DataType>; first->next = nullptr;//定义头指针初始化链表 Node<DataType>* r = first;//头指针的暂存指针,用来每次后移 Node<DataType>* s = nullptr;//待插入指针 for (int i = 0; i < n; i++) { s = new Node<DataType>; s->data = a[i];//待插入结点data域赋值 s->next = r->next; r->next = s;//在头结点后插入 r = s;//r指针移动到s的位置,完成后续操作 } r->next = nullptr;//r最后以为尾指针,尾指针next为空 }
?10.析构函数——销毁单链表
template <typename DataType> LinkList<DataType>::~LinkList() { Node<DataType>* p = first;//暂存头指针 while (first != nullptr) {//依次遍历 first = first->next; delete p;//释放空间 p = first;//工作指针后移 } }
2.4.4双链表
 data:数据域? ? ? ? prior:前驱指针域? ? ? ?next:后驱指针域
data:数据域? ? ? ? prior:前驱指针域? ? ? ?next:后驱指针域

1.插入操作?
?插入算法:
s->prior = p;//s前驱是p s->next = p->next;//s后继为p->next p->next->prior = s;//p->next的前驱是s p->next = s;//p的后继是s2.删除操作
算法分析:
p->prior-next = p-next;//先找p的前驱 p->next->prior = p->next;
2.4.5循环链表
在单链表中,如果将终端结点的指针有空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相连的单链表称为循环单链表
不带尾指针:

循环双链表
在双链表中,如果将终端结点的后继指针由空指针改为指向头节点,将头结点的前驱指针由空指针改为指向终端结点,就使整个双链表形成一个头尾

循环双链表:将终端结点的next指针由空指针改为指向头结点,
??????????????????????? 将头结点的prior指针由空指针改为指向终端结点
如果改用指向终端结点的尾指针(rear)来指示循环单链表,则查找开始节点与终端结点都很方便,存储地址分别是(rear->next)->next 和 rear。

2.5顺序表和链表的比较
1.存储分配方式存储分配方式
顺序表:采用顺序存储结构——静态存储分配,即用一段地址连续的存储单元依次存储线性表的数据元素,数据元素之间的逻辑关系通过存储位置(下标)来实现

?链表:采用链接存储结构——动态存储分配,即用一组任意的存储单元存放线性表的元素,用指针来反映数据元素之间的逻辑关系

?2.空间性能比较

 ?3.时间性能比较
?3.时间性能比较


从空间上讲,若线性表中元素个数变化较大或者未知,最好使用链表实现;如果用户事先知道线性表的大致长度,使用顺序表的空间效率会更高
从时间上讲,若线性表频繁查找却很少进行插入和删除操作,或其操作和元素在表中的位置密切相关时,宜采用顺序表作为存储结构;若线性表需频繁插入和删除时,则宜采用链表做存储结构
?2.6静态链表
2.6.1静态链表的存储结构
1.静态链表的存储
静态链表用数组来表示链表,用书元素的下标来模拟链表的指针域
avail是空闲链表头指针
first是静态链表头指针
静态链表的每个数组元素由两个域构成,data域存放数组元素,next域存放该元素的后继元素所在的数组下标(非指针类型)

?2.静态链表的实现
?插入操作:
在静态链表中进行插入操作,首先从空闲链的最前端摘下一个节点,将该节点插入即可
s = aivil;//将空闲结点赋值s aivil = list[aivil].next;//空闲指针后移 list[s].data = x;//将x填入下标为s的结点 list[s].next = list[p].next; list[p].next = s;//插入方法删除操作:
将被删除结点从静态链表摘下,再插入空闲链在最前端
删除算法:
q = list[p].next;//暂存被删除结点的下标 list[p].next = list[q].next;//摘链 list[q].next = avial;//将q插在avail处 avail = q;//空闲指针avail移动,此时q为空闲