学习前言:
树、森林与二叉树之间有一个自然的对应关系,即任何一棵树或一个森林都可唯一地对应于一棵二叉树,而任何一棵二叉树也能唯一地对应于一个森林或一棵树。

话不多说,就让我们抓紧开始吧~
今日学习目标:
把“树与二叉树的转换”给我拿下!
今日学习相关知识点:
- 学习前需要明白一个原理:树中每个结点至多只有一个最左边的孩子(长子)和一个右邻的兄弟。(简单来说,一个结点的左边是这个结点的儿子,右边的是这个结点的兄弟)
今日学习过程:
树的定义:是由n(n≥1)个有限节点组成一个具有层次关系的集合。
如图所示就是一棵树:

那现在如何进行树与二叉树的转换呢?
下面我就简单举一个案例,看完一定会有不少的收获!
【案例】现将这棵树进行转换成二叉树,并且对它进行前序遍历和后序遍历。
【分析】
A这个根结点下的子结点:B、E、K
B这个根结点下的子结点:C、D
E这个根结点下的子结点:F、G、H
G这个根结点下的子结点:I、J
(换句话说,这些子结点在同一个父结点中是兄弟关系)
现在,我们只保留根结点下面最左边的线,其他的线删除;兄弟结点之间用用蓝色线链接
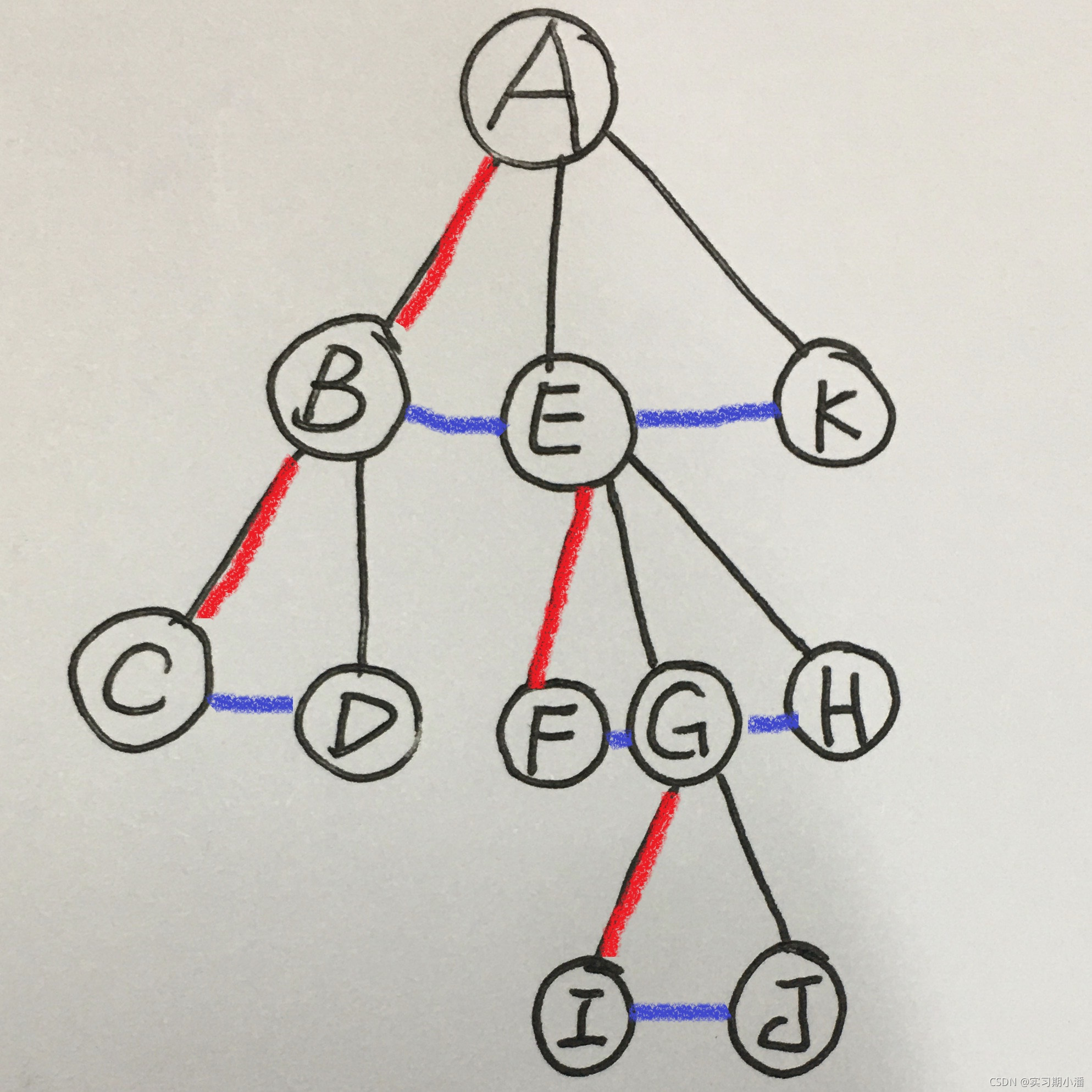
(激动人心的时刻到来啦~)现在就可以进行转换成二叉树了!
我们首先对二叉树的形状是有一定了解的基础下,其次把红线的放在根结点左边,蓝线放在根结点的右半边。
树的遍历规则(如下)与二叉树的遍历稍有不同:
前序遍历一棵树等价于前序遍历该树对应的二叉树;
后序遍历一棵树等价于中序遍历该树对应的二叉树。
前序遍历(根—左—右):A B C D E F G I J H K
后序遍历(左—根—右):C D B F I J G H E K A
(后序遍历时要小心F的顺序!)
希望看完这篇博客对你有一定的帮助哦!



