[数据结构与算法]【数据结构与算法】栈与队列【C语言版】

3.1 栈和队列的定义和特点

栈

队列

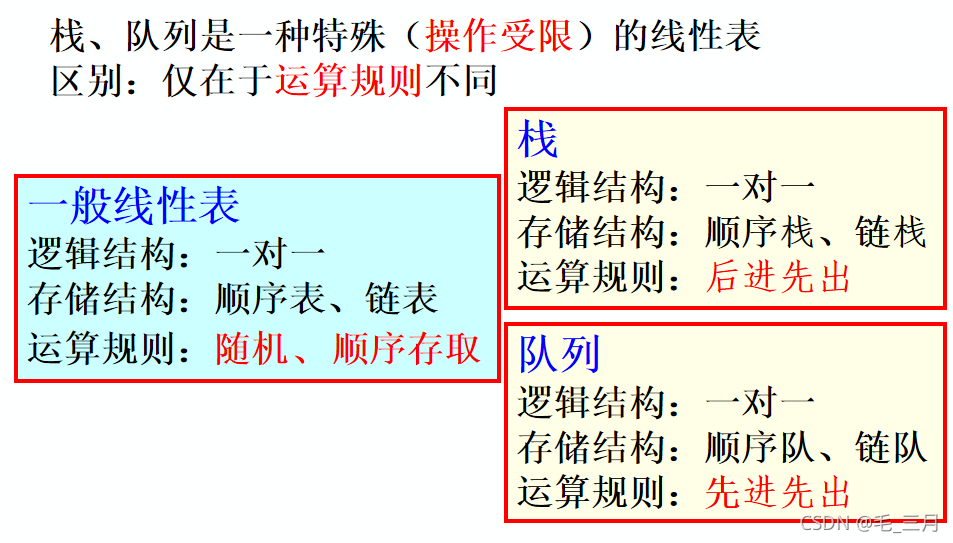
3.2 栈、队列与一般线性表的区别

3.3 栈的表示和操作的实现

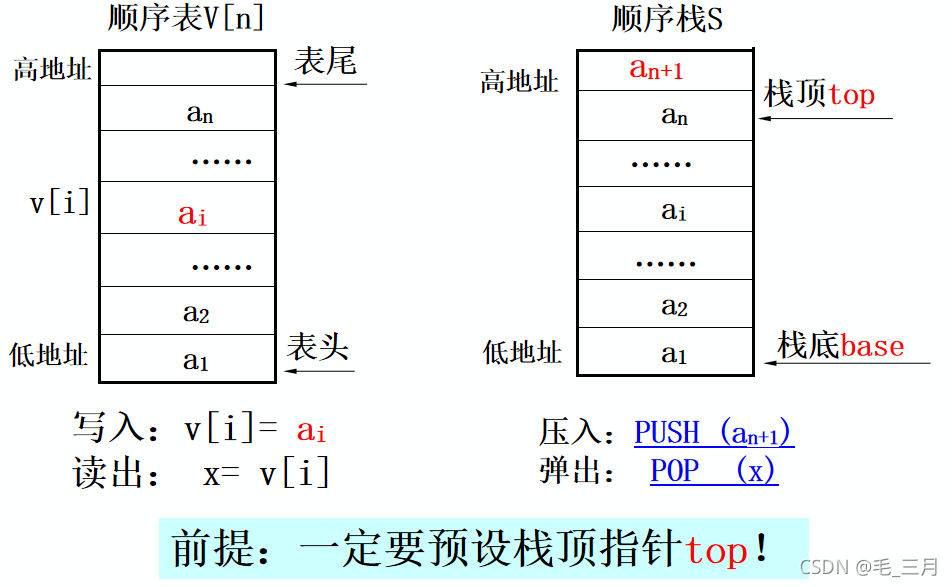
顺序栈与顺序表

=================

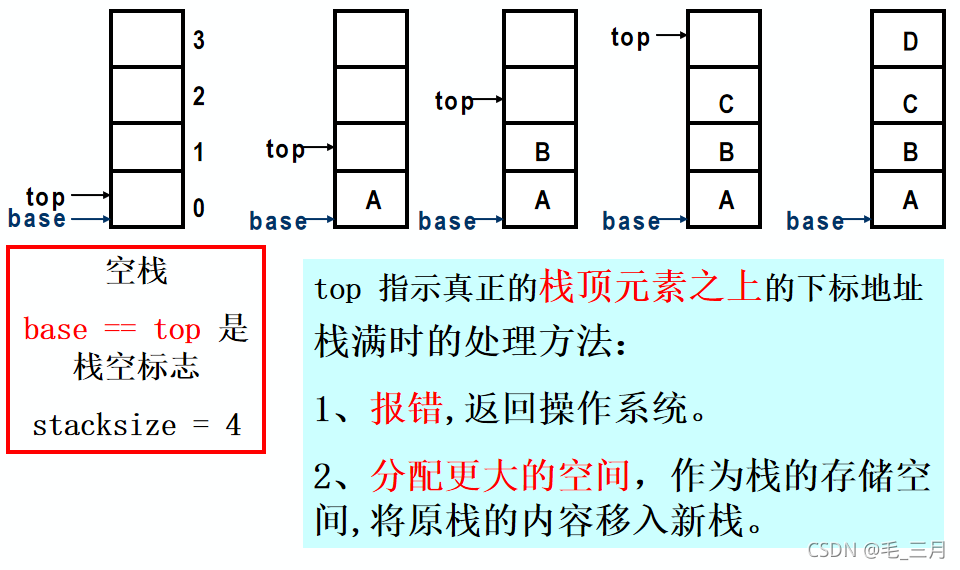
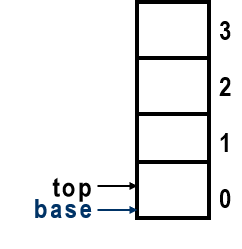
顺序栈的表示

#define  MAXSIZE  100
typedef struct
{
		SElemType   *base;
		SElemType   *top;
		int stacksize;
}SqStack;

顺序栈初始化

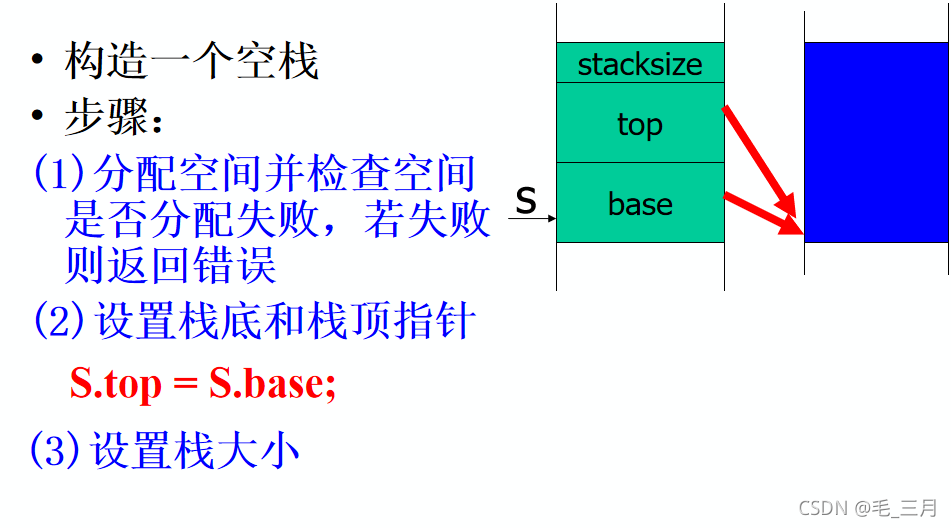
Status InitStack( SqStack &S )
{
	S.base =new SElemType[MAXSIZE]；
	if( !S.base ) 	return OVERFLOW;
	S.top = S.base;
	S.stackSize = MAXSIZE;
	return OK;
}

判断顺序栈是否为空

bool StackEmpty( SqStack S )
{
	if(S.top == S.base) return true;
   else return false;
}

求顺序栈的长度

int StackLength( SqStack S )
{
	return S.top – S.base;
}

清空顺序栈

Status ClearStack( SqStack S )
{
	if( S.base ) S.top = S.base;
	return OK;
}

销毁顺序栈

Status DestroyStack( SqStack &S )
{
	if( S.base )
	{
		delete S.base ;
		S.stacksize = 0;
		S.base = S.top = NULL;
	}
  return OK;
}

顺序栈进栈

(1)判断是否栈满，若满则出错
(2)元素e压入栈顶
(3)栈顶指针加1

Status Push( SqStack &S, SElemType e)  
{
	if( S.top - S.base== S.stacksize ) // 栈满
        return ERROR; 	
	*S.top++=e;
	return OK;
}

顺序栈出栈

(1)判断是否栈空，若空则出错
(2)获取栈顶元素e
(3)栈顶指针减1

Status Pop( SqStack &S, SElemType &e)  
{
	if( S.top == S.base ) // 栈空
        return ERROR; 	
	e＝ *--S.top;
	return OK;
}

取顺序栈栈顶元素

• 判断是否空栈，若空则返回错误
• 否则通过栈顶指针获取栈顶元素

Status GetTop( SqStack S, SElemType &e)  
{
	if( S.top == S.base )	 return ERROR; 	// 栈空
	e = *( S.top – 1 );
	return OK;
}

// 注意： 不能为 e = *( S.top -- );   自己思考原因

==================

链栈的表示

typedef  struct StackNode {
      SElemType  data;
      struct StackNode *next;
 } StackNode,  *LinkStack;
LinkStack S;   

链栈的初始化

void InitStack(LinkStack &S )
{
	S=NULL;
}

判断链栈是否为空

Status StackEmpty(LinkStack S)
  {   
	if (S==NULL) return TRUE;   
	else return FALSE;
  }

链栈进栈

Status Push(LinkStack &S , SElemType e)
  {  
   p=new StackNode;      //生成新结点p   
   if (!p) exit(OVERFLOW);  
   p->data=e; p->next=S; S=p; 
   return OK; }

链栈出栈

Status Pop (LinkStack &S,SElemType &e)
{if (S==NULL) return ERROR;
 e = S-> data;  p = S;   S =  S-> next;
 delete p;   return OK;  }  

取链栈栈顶元素

SElemType GetTop(LinkStack S)
   {
       if (S==NULL) exit(1)；   else return S–>data;
    }

3.4 　栈与递归

递归的定义

若一个对象部分地包含它自己, 或用它自己给自己定义, 则称这个对象是递归的；

若一个过程直接地或间接地调用自己, 则称这个过程是递归的过程。

long Fact ( long n ) {
    if ( n == 0) return 1;
    else return n * Fact (n-1); }

以下三种情况常常用到递归方法

1. 递归定义的数学函数
2. 具有递归特性的数据结构
3. 可递归求解的问题

1. 递归定义的数学函数:

2. 具有递归特性的数据结构:

3. 可递归求解的问题:

• 迷宫问题
• Hanoi塔问题

递归算法的效率分析

递归的优缺点

优点：结构清晰，程序易读

缺点：每次调用要生成工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。

3.5 　队列的表示和操作的实现

队列的抽象数据类型

队列的顺序表示－－用一维数组base[M]

#define M  100   //最大队列长度
Typedef struct {
   QElemType *base;  //初始化的动态分配存储空间
   int  front;            //头指针   
   int  rear;             //尾指针
}SqQueue;  

存在的问题 设大小为M

解决的方法－－循环队列

base[0]接在base[M-1]之后
若rear+1==M
则令rear=0;

实现：利用“模”运算
入队：
  base[rear]=x;
  rear=(rear+1)%M;
出队：
  x=base[front];
  front=(front+1)%M; 

循环队列

#define MAXQSIZE  100  //最大长度
Typedef struct {
   QElemType *base;  //初始化的动态分配存储空间
   int  front;            //头指针   
   int  rear;             //尾指针
}SqQueue;  

循环队列初始化

Status InitQueue (SqQueue &Q){
    Q.base =new QElemType[MAXQSIZE] 
   if(!Q.base) exit(OVERFLOW);
    Q.front=Q.rear=0;
    return OK;
}

求循环队列的长度

int  QueueLength (SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;                             
 }

循环队列入队

Status EnQueue(SqQueue &Q,QElemType e){
    if((Q.rear+1)%MAXQSIZE==Q.front)  return ERROR;
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXQSIZE;
     return OK;
}

循环队列出队

Status DeQueue (LinkQueue &Q,QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.base[Q.front];
   Q.front=(Q.front+1)%MAXQSIZE;
   return OK;
}

=============

链队列

typedef struct QNode{
   QElemType   data;
   struct Qnode  *next;
}Qnode, *QueuePtr;
typedef struct {
   QueuePtr  front;            //队头指针   
   QueuePtr  rear;             //队尾指针
}LinkQueue;  

链队列初始化

Status InitQueue (LinkQueue &Q){
   Q.front=Q.rear=(QueuePtr) malloc(sizeof(QNode)); 
    if(!Q.front) exit(OVERFLOW);
    Q.front->next=NULL;
     return OK;
}

销毁链队列

Status DestroyQueue (LinkQueue &Q){
   while(Q.front){
      Q.rear=Q.front->next;
      free(Q.front);
      Q.front=Q.rear;   }    
   return OK;
}

判断链队列是否为空

Status QueueEmpty (LinkQueue Q){
    return (Q.front==Q.rear);                             
 }

求链队列的队头元素

Status GetHead (LinkQueue Q, QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.front->next->data;
   return OK;
}

链队列入队


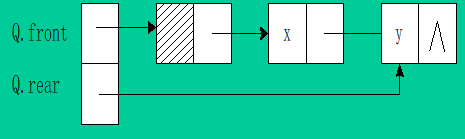
Status EnQueue(LinkQueue &Q,QElemType e){
    p=(QueuePtr)malloc(sizeof(QNode));
    if(!p) exit(OVERFLOW);
    p->data=e; p->next=NULL;
    Q.rear->next=p;
    Q.rear=p;
    return OK;
}

链队列出队

Status DeQueue (LinkQueue &Q,QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   p=Q.front->next;
   e=p->data;
   Q.front->next=p->next;
   if(Q.rear==p) Q.rear=Q.front;
   delete p;
   return OK;
}

3.6 案例分析与实现

案例3.1 ：数制的转换

【算法步骤】
① 初始化一个空栈S。
② 当十进制数N非零时，循环执行以下操作：

• 把N与8求余得到的八进制数压入栈S；
• N更新为N与8的商。

③ 当栈S非空时，循环执行以下操作：

• 弹出栈顶元素e；
• 输出e。

【算法描述】
void conversion(int N)
{//对于任意一个非负十进制数，打印输出与其等值的八进制数
   InitStack(S);	//初始化空栈S
   while(N)	//当N非零时,循环
   {
      Push(S,N%8);	//把N与8求余得到的八进制数压入栈S
      N=N/8;		//N更新为N与8的商
   }
   while(!StackEmpty(S))//当栈S非空时，循环
   {
      Pop(S,e);		//弹出栈顶元素e
      cout<<e;		//输出e
   }
}

案例3.2 ：括号的匹配