[数据结构与算法]斐波那契数列的五种实现方式

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。

暴力递推

class Solution {
    public int fib(int n) {
        if(n==0)return 0;
        else if(n==1)return 1;
        else return fib(n-1)+fib(n-2);
    }
}

此方法最直观，但存在许多重复计算，时间复杂度为O(2^n)。

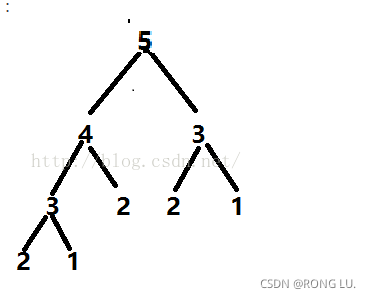
记忆化搜索

暴力递归存在很多重复计算，我们定义一个数组用来保存已经计算出的值，如果需要算某一项斐波那契数列的值，直接从数组里取，数组不存在的话在进行计算。

class Solution {
    int[]memory;
    public int fib(int n) {
        if(n<2)return n;
        memory=new int[n+1];
        Arrays.fill(memory,-1);//用-1填充记忆数组表示未记录
        memory[0]=0;
        memory[1]=1;
        return dfs(n);
    }
    public int dfs(int n){
        if(memory[n]!=-1)return memory[n];
        int a=dfs(n-2);
        int b=dfs(n-1);
        memory[n]=a+b;//存储
        return memory[n];
    }
}

动态规划

再记忆化搜索上继续优化，得到动态规划的结果

class Solution {
    public int fib(int n) {
    if(n<2)return n;
    int[]dp=new int[n+1];
    dp[0]=0;
    dp[1]=1;
    for(int i=2;i<=n;i++){
        dp[i]=dp[i-1]+dp[i-2];
    }
    return dp[n];
    }
}

时间复杂度O(n)
空间复杂度O(n)

滚动数组优化动态规划

在动态规划中，如果状态转移方程完全由上一层的状态转移而来，这样我们只需要保存上一层的状态即可递推出本层的状态，便可以用滚动数组的方式来对空间复杂度进行优化。

class Solution {
    public int fib(int n) {
    if(n<2)return n;
    int first=0;
    int second=1;
    int result=0;
    for(int i=2;i<=n;i++){
        result=first+second;
        first=second;
        second=result;
    }
    return result;
    }
}

时间复杂度O（n）
空间复杂度O（1）

矩阵快速幂

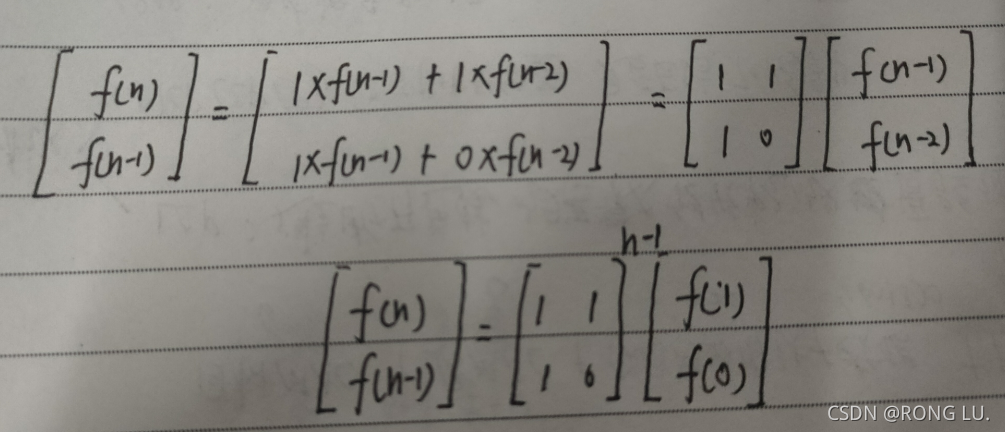
class Solution {
    public int fib(int n) {
        if(n<2)return n;
        int[][]res=new int[][]{{1},{0}};
        int[][]mat=new int[][]{{1,1},{1,0}};
        n--;
        //快速幂算法
        while(n>0){
            if(n%2==1)res=mul(res,mat);
            
                mat=mul(mat,mat);
                n>>=1;
            
        }
        return res[0][0];
        
    }
    //定义矩阵相乘方法
    public int[][] mul(int[][]a,int[][]b){
        int r=a.length;
        int c=b[0].length;
        int n=a[0].length;
        int[][]res=new int[r][c];
        for(int i=0;i<r;i++){
            for(int j=0;j<c;j++){
                for(int k=0;k<n;k++){
                    res[i][j]+=a[i][k]*b[k][j];
                }
            }
        }
        return res;
    }
}

时间复杂度O(logn)
空间复杂度O(1)