matlab爱好者。
求解第一类边值问题的四种方法(完整),包括相互的验证:
任何第一类边值问题都可以用这四种方法快速解决。矩阵法这里只能适用于5个离散点,想得到通解请自己推一遍矩阵法。
我们以一道例题开始:
题目:
解法:①初值解法解边值:通过给dy来求y(end),直到拟合。首先做一个函数,给一个dy,返回一个y(end)。
函数名为findf,
如下:
function s=findf(dy)
t=linspace(0,4,11);
dt=t(2)-t(1);
y(1)=0; v(1)=dy;
for i=1:length(t)-1
y(i+1)=y(i)+v(i)dt;
v(i+1)=v(i)+(2v(i)cos(t(i))-y(i)sin(4t(i))-cos(3t(i)))dt;
end
s=y(end);
程序源代码:
clear
x=linspace(0,2,10);
for i=1:length(x)
ss(i)=findf(x(i));
end
plot(x,ss)
hold on;
o=linspace(0,2,10);
for j=1:length(o)
g(j)=2;
end
plot(o,g,’-’);
xlabel(‘dy’);
ylabel(‘y(end)’);
title(‘y(end)-dy’);
grid on;
legend(‘y(end)’,‘y(end)=2’);
得到结果: 再做一个图,就是每给定一个dy时候,y的图像:
再做一个图,就是每给定一个dy时候,y的图像:
源代码:
clear
k=linspace(0,4,100);
for l=1:length(k)
[y,t]=findf(k(l));
plot(t,y,’-’)
hold on;
end
hold on;
o=linspace(0,4,10);
for j=1:length(o)
g(j)=2;
end
plot(o,g,’-o’);
findf函数为:
function [y,t]=findf(dy)
t=linspace(0,4,11);
dt=t(2)-t(1); y(1)=0; v(1)=dy;
for i=1:length(t)-1
y(i+1)=y(i)+v(i)dt;
v(i+1)=v(i)+(2v(i)cos(t(i))-y(i)sin(4t(i))-cos(3t(i)))dt;
end
结果图: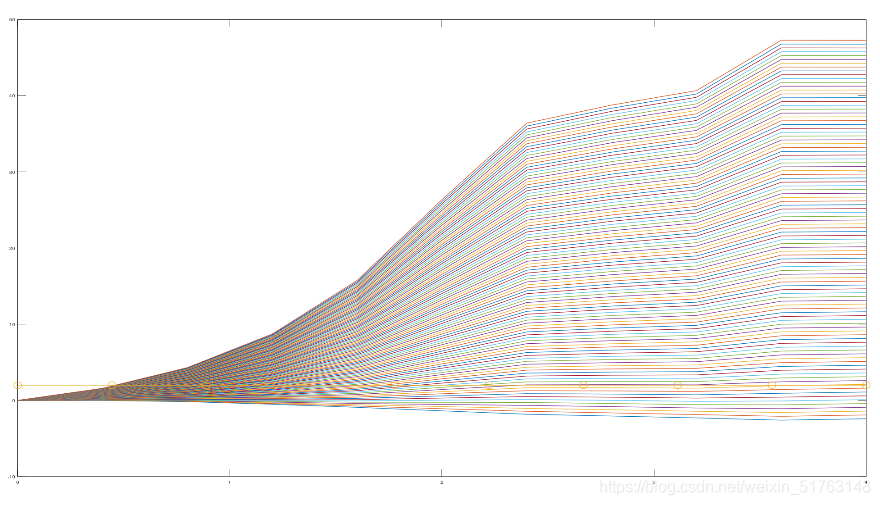
②割线法源代码:
clear
t(1)=1;t(2)=2;i=2;
while abs(t(i)-t(i-1))>0.01 f(i)=findf(t(i))-2; f(i-1)=findf(t(i-1))-2; t(i+1)=t(i)-(f(i)(t(i)-t(i-1)))/(f(i)-f(i-1)); i=i+1;
end
plot(t,’-o’)
findf函数为:
function s=findf(dy)
t=linspace(0,4,11);
dt=t(2)-t(1); y(1)=0; v(1)=dy;
for i=1:length(t)-1
y(i+1)=y(i)+v(i)dt;
v(i+1)=v(i)+(2v(i)cos(t(i))-y(i)sin(4t(i))-cos(3t(i)))dt;
end
s=y(end);
结果: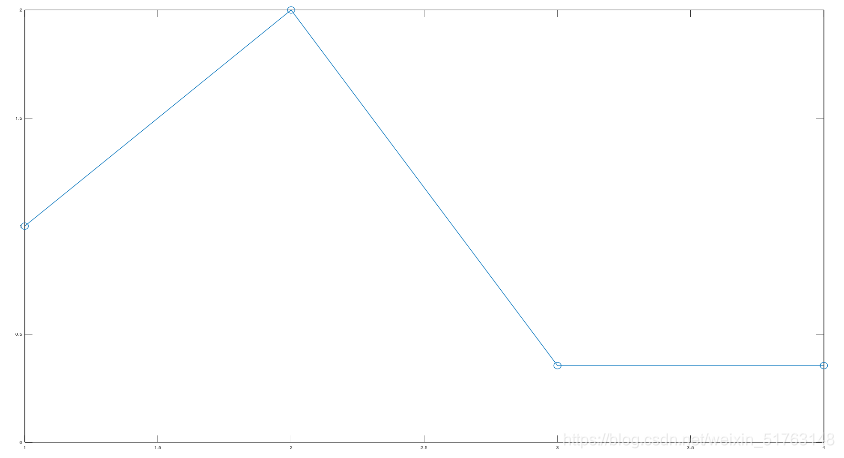
左端导数值为0.35462。
用①方法来验证割线法结果是否正确,不要轻易相信结果,我们写个代码来验证一下:验证源代码:
clear
[y,t]=findf(0.35462);
plot(t,y,’-’);
hold on;
o=linspace(0,4,10);
for j=1:length(o)
g(j)=2;
end
plot(o,g,’-o’);
其中findf函数源代码:
function [y,t]=findf(dy)
t=linspace(0,4,11);
dt=t(2)-t(1);
y(1)=0; v(1)=dy;
for i=1:length(t)-1
y(i+1)=y(i)+v(i)dt;
v(i+1)=v(i)+(2v(i)cos(t(i))-y(i)sin(4t(i))-cos(3t(i)))dt;
end
结果: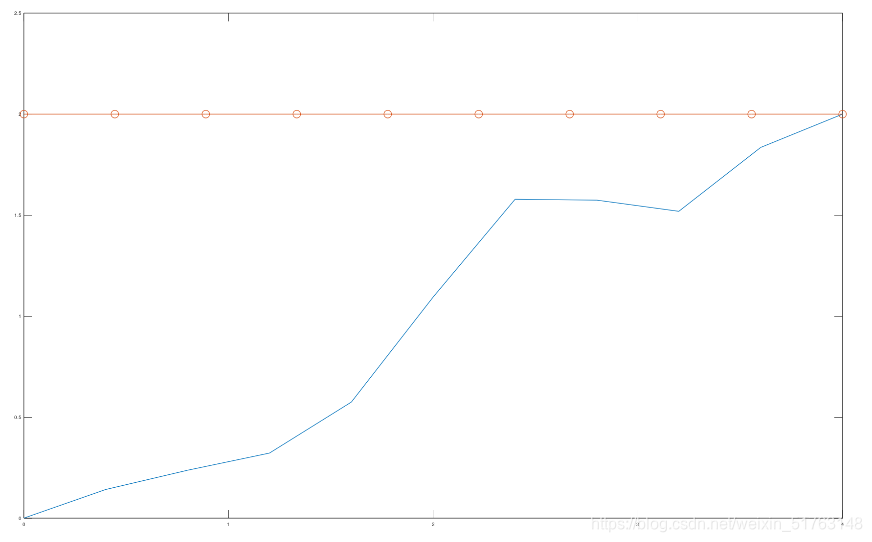
发现在0.35462的结果下,最后一个值确实是2,故这个结果是没有问题的。注:如果要用这种方法计算右端导数,我们已经已知左端点导数值了,所以已经简化为初值问题,这里没必要再赘述。
③自洽法源代码:
clear
t=linspace(0,4,10);
dt=t(2)-t(1);
y=zeros(1,10);
y(1)=1;y(end)=2;delta=1;i=1;
while delta>0.01&&i<1000
g=y;
for i=2:length(t)-1
g(i)=0.5(y(i+1)+y(i-1)-(dt^2)(2((y(i+1)-y(i-1))/(2dt))cos(t(i))-y(i)sin(4t(i))-cos(3t(i))));
end
delta=sum(abs(y-g)); y=g; i=i+1;
end
结果: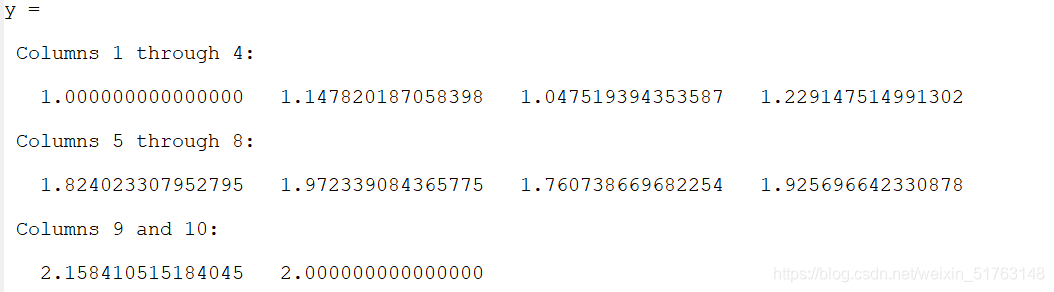
④矩阵法,将t离散化成5个点的案例。
源代码:
clear
p=[1 0 0 0 0;1+cos(1) -2+sin(4) 1-cos(1) 0 0;0 1+cos(2) -2+sin(8) 1-cos(2) 0;0 0 1+cos(3) -2+sin(12) 1-cos(3);0 0 0 0 1];
q=[1;-cos(3);-cos(6);-cos(9);2];
y=inv(p)q
结果:
用自洽法来验证矩阵法的结果是否正确,不能简单以为这个结果就是正确的。所以我们来用自洽法来验证一下:
源代码:
clear
t=linspace(0,4,5);
dt=t(2)-t(1);
y=zeros(1,5);
y(1)=1;y(end)=2;delta=1;i=1;
while delta>0.01&&i<1000
g=y;
for i=2:length(t)-1
g(i)=0.5(y(i+1)+y(i-1)-(dt^2)(2*((y(i+1)-y(i-1))/(2*dt))cos(t(i))-y(i)sin(4t(i))-cos(3t(i))));
end
delta=sum(abs(y-g)); y=g; i=i+1;
end
结果:
五个离散点的时候自洽法求得的结果和矩阵法一模一样。故矩阵法和自洽法互相验证
注:有一些matlab里面的乘号被屏蔽掉了,请自行添加,否则无法运行。
编者水平不高,若有错误,请评论区指正
谢谢。