[数据结构与算法]线性表基础OJ入门

🗻一、顺序表

🏟?1. 移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

思路1：双指针法

right指针用来遍历数组 left指针用来更改数组元素 如果right指针指的值不等于val 那么a[left]=a[right],left right都向前移动一位，如果right指的值是val，那么right移动一位，left不动，right移动到最后一位后，最终left的值就是数组的长度。

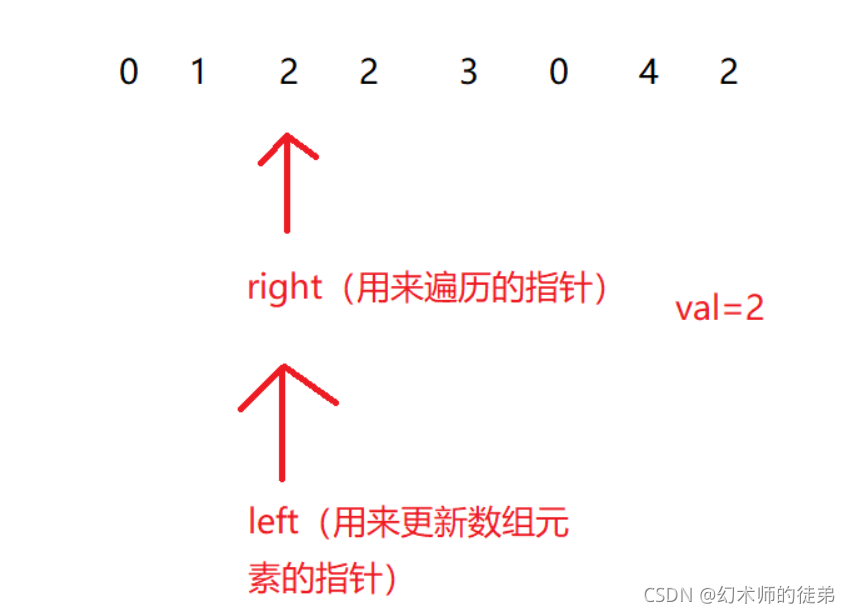
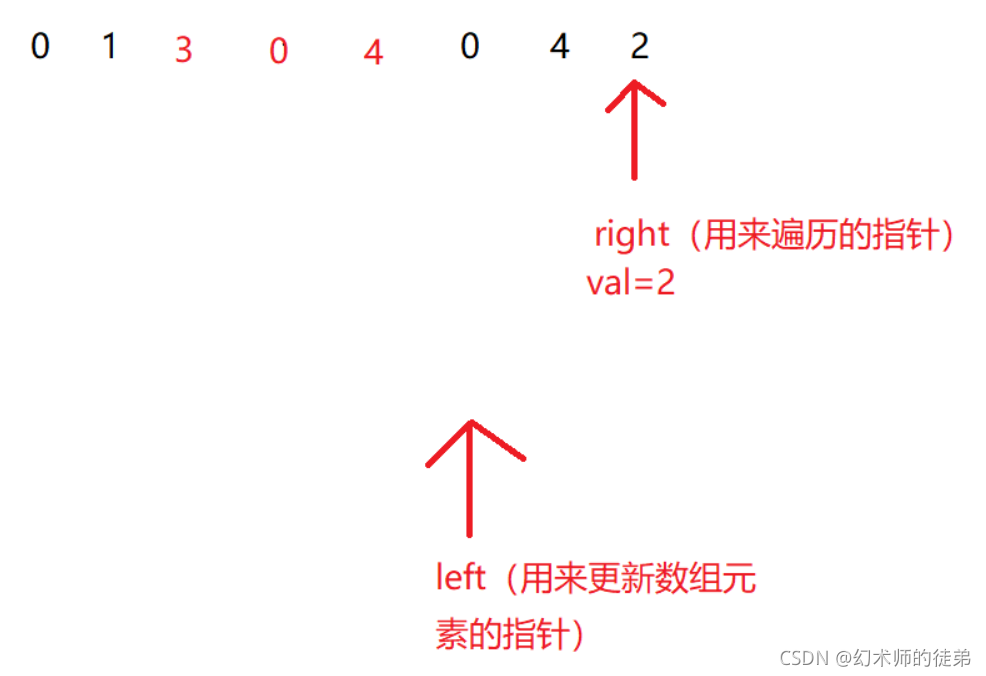
所以源码如下：

int removeElement(int* nums, int numsSize, int val)
{
    int left=0;
    int right=0;
    //双指针法，让右边的指针遍历数组，如果右指针遇到的值不等于val
    //就把他的值写到左指针的位置上
    for(right=0;right<=numsSize-1;right++)
    {
        if(nums[right]!=val)
        {
            nums[left]=nums[right];
            left++;
        }
    }
    return left;
}

🏖?思路2:改良版双指针

??题目中并未要求数组元素要保持原来的顺序，所以让一个指针right从右边开始，一个指针从左边开始，如果a[left]的值是val，就让a[left]=a[right],然后right–，如果不是则left++,当left=right时结束循环。

int removeElement(int* nums, int numsSize, int val)
{
    int left=0;
    int right=numsSize-1;
    while(left<=right)
    {
        if(nums[left]==val)
        {
            nums[left]=nums[right];
            right--;
        }
        else
        {
            left++;
        }
    }
    return left;
}

🕋2.删除数组中的重复元素

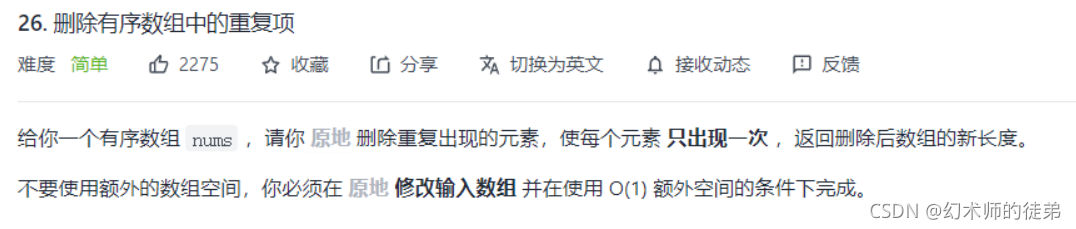
思路：双指针法

一个指针right用来遍历数组，left用来填写数组，如果right前继的值和right的值不相等，那么a[left]=a[right]，left++，right++，如果相等，那么right++。

int removeDuplicates(int* nums, int numsSize)
{
    if(numsSize==0)
    {
        return 0;
    }
    int left=1;
    int right=1;
    for(right=1;right<numsSize;right++)
    {
        if(nums[right-1]!=nums[right])
        {
            nums[left]=nums[right];
            left++;
        }
    }
    return left;
}

🌁3.合并有序数组

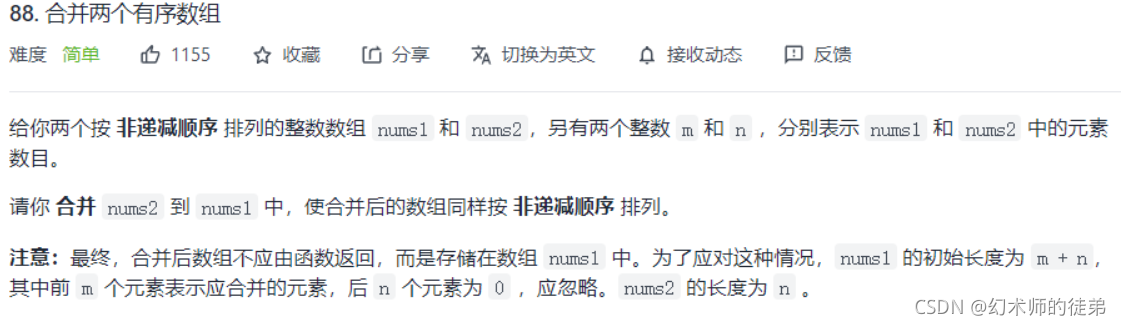
思路1：把nums2放到nums1中，然后用一个排序算法，最佳的时间复杂度是o(NlogN)

void bubblesort(int* nums,int number)
{
    for(int i=0;i<number-1;i++)
    {
        for(int j=0;j<number-1-i;j++)
        {
            if(nums[j]>nums[j+1])
            {
                int temp=nums[j];
                nums[j]=nums[j+1];
                nums[j+1]=temp;
            }
        }
    }
}
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
    for(int i=m;i<m+n;i++)
    {
        nums1[i]=nums2[i-m];
    }
    bubblesort(nums1,m+n);
}

思路2：双指针法

两个指针在nums1里头和nums2里头遍历 取出较小者放到 新数组arr里头 最后把新数组赋给nums1，这种解法空间复杂度是O(n)

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
    //双指针1 
    //两个指针在nums1里头和nums2里头遍历 取出较小者放到 新数组arr里头 最后把新数组赋给nums1
    int arr[m+n];
    int left=0;
    int right=0;
    while(left<m || right <n)
    {
        if(left==m)//如果left已经结束
        {
            arr[left+right]=nums2[right];
            right++;
        }
        else if(right==n)//如果right已经结束
        {
            arr[left+right]=nums1[left];
            left++;
        }
        else if(nums1[left]<nums2[right])
        {
            arr[left+right]=nums1[left];
            left++;
        }
        else
        {
            arr[left+right]=nums2[right];
            right++;
        }
    }
     for(int i=0;i<m+n;i++)
    {
        nums1[i]=arr[i];
    }
}

思路3:双指针法尾插

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
    //双指针解法2 取两者的大者放到数组nums1的后头
    //放第k个时候 最差情况下nums1一个还没取出来 此时k<=n 完全足够放到nums1后面而不影响nums1前面的空间
    //好处是节约了空间。
    int end=m+n-1;
    int p1=m-1;
    int p2=n-1;
    for(end=m+n-1;end>=0;end--)
    {
        if(p1==-1)
        {
            nums1[end]=nums2[p2];
            p2--;
        }
        else if(p2==-1)
        {
            nums1[end]=nums1[p1];
            p1--;
        }
        else if(nums1[p1]>nums2[p2])
        {
            nums1[end]=nums1[p1];
            p1--;
        }
        else
        {
            nums1[end]=nums2[p2];
            p2--;
        }
    }
}

🚇二、链表

🛸1.移除链表元素

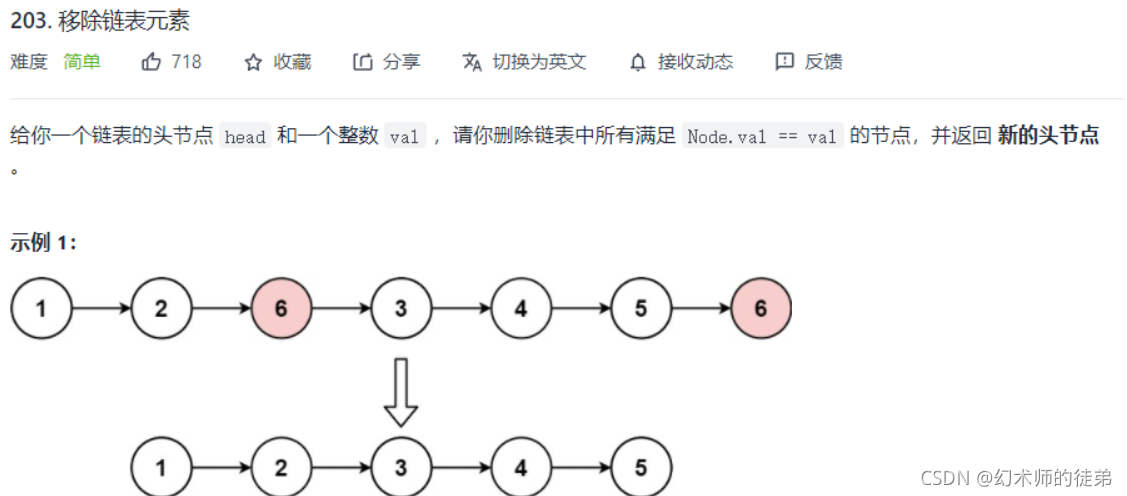
思路1.暴力解法

注意头删和中间删除操作不同

void pop(struct ListNode* head,struct ListNode* p)
{
    struct ListNode* q=head;
    while(q->next!=p)
    {
        q=q->next;
    }
    q->next=p->next;
    free(p);
}
struct ListNode* removeElements(struct ListNode* head, int val)
{
    if(head==NULL)
    {
        return head;
    }
    while(head!=NULL && head->val==val)
    {
        struct ListNode* tmp=head;
        head=head->next;
        free(tmp);
    }
    struct ListNode* p=head;
    while(p)
    {
        if(p->val==val)
        {
            struct ListNode* tmp=p->next;
            //删除p位置的元素
            pop(head,p);
            p=tmp;
        }
        else
        {
            p=p->next;
        }
    }
    return head;
}

2.双指针法

一个指针q表示p的前继，一个指针p遍历链表

struct ListNode* removeElements(struct ListNode* head, int val)
{
    struct ListNode* p=head;
    struct ListNode* q=NULL;
    while(p)
    {
        //1.头删
        if(head->val==val)
        {
            head=head->next;
            free(p);
            p=head;
        }
        //2.中间删除
        else
        {
            if(p->val==val)
            {
                q->next=p->next;
                free(p);
                p=q->next;
            }
            else
            {
                q=p;
                p=p->next;
            }
        }
    }
    return head;
}

🎇2.逆置单链表

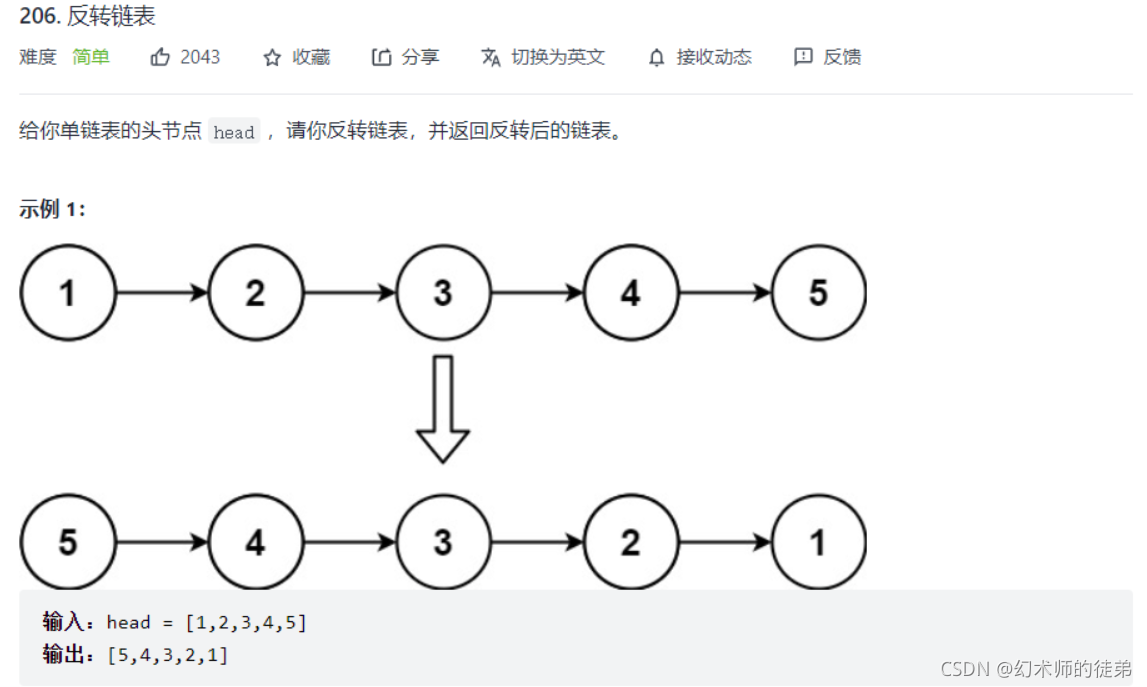
思路1：原地翻转

三个指针 ，指向一个节点的前继，指向这个节点，指向这个节点的后继，翻转只要把当前节点的next指向这个节点的前继，然后这个指针走到这个节点的后继，然后前继走到这个节点，然后后继走到下一个位置，

struct ListNode* reverseList(struct ListNode* head)
{
    if(head!=NULL)
    {
        //p1是p2的前继
        //p2是正要反转的节点的指针
        //p3是p2的后继的指针 为了保证能够迭代
        struct ListNode* p1=NULL;
        struct ListNode* p2=head;
        struct ListNode* p3=p2->next;
        while(p2->next!=NULL)
        {
            p2->next=p1;
            p1=p2;
            p2=p3;
            p3=p3->next;
        }
        p2->next=p1;
        head=p2;
    }
    return head;
}

思路2：头插法

struct ListNode* reverseList(struct ListNode* head){
    //思路 取链表中的节点 头插到新链表中
    struct ListNode* cur=head;
    struct ListNode* newhead=NULL;
    while(cur)
    {
        struct ListNode* next=cur->next;
        cur->next=newhead;
        newhead=cur;
        cur=next;
    }
    return newhead;
}

🪂3.链表的中间结点

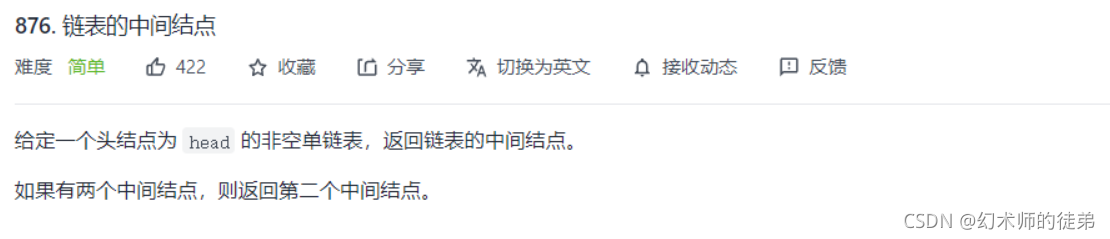
1.暴力解法：

先遍历一遍链表得到链表长度，然后再走一半长度就行。

struct ListNode* middleNode(struct ListNode* head)
{
    int num=0;
    struct ListNode* test=head;
    while(test!=NULL)
    {
        test=test->next;
        num++;
    }
    test=head;
    for(int i=1;i<=num/2;i++)
    {
        test=test->next;
    }
    return test;
}

2.快慢指针法

利用相对速度，一个指针一次只能走一步，另一个一次可以走两步，当后面那个指针走到了末尾的时候，第一个指针就指向了中间的位置。

//快慢指针法
struct ListNode* middleNode(struct ListNode* head){
    //中间节点，所以我们利用两个指针 一个fast一个slow 
    //slow一次走一步
    //fast一次走两步
    //画图得知奇数情况fast最后走到结尾
    //偶数情况fast走到null
    struct ListNode* fast=head;
    struct ListNode* slow=head;
    while(fast!=NULL && fast->next!=NULL)//两个有一个为空结束
    {
        fast=fast->next->next;
        slow=slow->next;
    }
    return slow;
}

🎢4.链表的倒数第k个结点

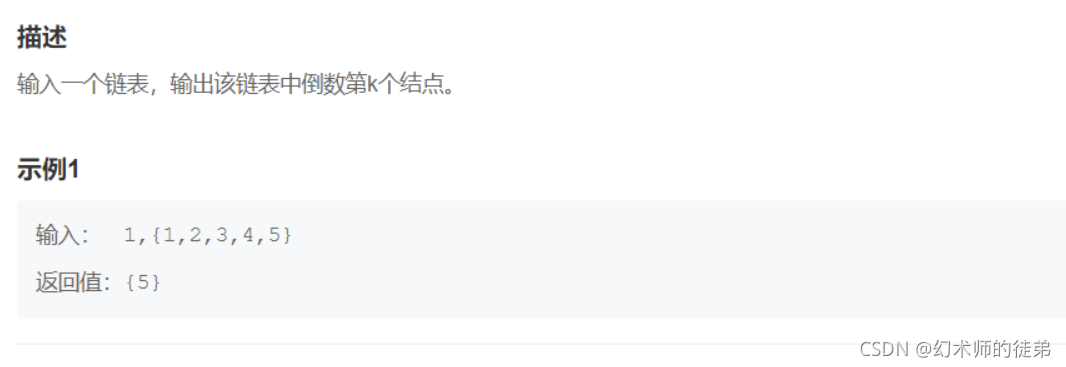
思路1.暴力求解

先遍历一遍数组，得到链表长度nums，然后倒数第k个结点就是走nums-k步。

注意k>nums时就越界了。

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
    struct ListNode* ret=pListHead;
    int nums=0;
    while(ret)
    {
        ret=ret->next;
        nums++;
    }
    if(k>nums)
        return NULL;
    ret=pListHead;
    for(int i=1;i<=nums-k;i++)
    {
        ret=ret->next;
    }
    return ret;
}

思路2.双指针法
要走倒数第k个元素 我可以让一个指针先走k步
然后第一个指针和后面的指针一起走
第一个指针走到NULL 那么第一个指针就走到了倒数第k个

因为这样第一个指针第二轮就是走了n-k步，所以第二个指针也走了n-k步到达了目标结点。

注意在走k步时，

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
    //思路 双指针
    //要走倒数第k个元素 我可以让一个指针先走k步
    //然后第一个指针和后面的指针一起走
    //第一个指针走到NULL 那么第一个指针就走到了倒数第k个
    struct ListNode* slow=pListHead;
    struct ListNode* fast=pListHead;
    for(int i=1;i<=k ;i++)
    {
        if(fast==NULL)
        {
            return NULL;
        }
        fast=fast->next;
    }
    while(fast)
    {
        fast=fast->next;
        slow=slow->next;
    }
    return slow;
}

🏰5.合并两个有序链表

思路1.双指针暴力解法

两个指针用来遍历两个链表，小的元素尾插到我们的新链表中，如果有一个链表的指针到了null了，就把新链表的尾巴连上剩下的那个链表。

struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
    if(l1==NULL)
    //有一个为空直接返回另一个
    {
        return l2;
    }
    if(l2==NULL)
    {
        return l1;
    }
    struct ListNode* newlist=NULL;
    struct ListNode* tail=NULL;
    //newlist还是空的时候要更新头指针的值
    if(l1->val<l2->val)
    {
        newlist=l1;
        l1=l1->next;
        tail=newlist;
    }
    else
    {
        newlist=l2;
        l2=l2->next;
        tail=newlist;
    }
    //其他时候都尾插法
    while(l1!=NULL && l2!=NULL)
    {
        if(l1->val<l2->val)
        {
            tail->next=l1;
            tail=l1;
            l1=l1->next;
        }
        else
        {
            tail->next=l2;
            tail=l2;
            l2=l2->next;
        }
    }
    if(l1==NULL)
    {
        tail->next=l2;
    }
    if(l2==NULL)
    {
        tail->next=l1;
    }
    return newlist;
}

思路2 利用哨兵位来简化双指针法

struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
    if(l1==NULL)
    {
        return l2;
    }
    if(l2==NULL)
    {
        return l1;
    }
    struct ListNode* newlist=(struct ListNode*)malloc(sizeof(struct ListNode));
    struct ListNode* tail=newlist;
    while(l1!=NULL && l2!=NULL)
    {
        if(l1->val<l2->val)
        {
            tail->next=l1;
            tail=l1;
            l1=l1->next;
        }
        else
        {
            tail->next=l2;
            tail=l2;
            l2=l2->next;
        }
    }
    if(l1==NULL)
    {
        tail->next=l2;
    }
    if(l2==NULL)
    {
        tail->next=l1;
    }
    struct ListNode* ret=newlist->next;
    free(newlist);
    return ret;
}

🕍6.链表分割

思路是两个链表 一个尾插比它小的，另一个尾插比它大的 然后把这两个链表连起来

class Partition {
public:
    ListNode* partition(ListNode* pHead, int x) {
        ListNode* smallhead=(ListNode*)malloc(sizeof(ListNode));
        ListNode* bighead=(ListNode*)malloc(sizeof(ListNode));
        smallhead->next=NULL;
        ListNode* smalltail=smallhead;
        bighead->next=NULL;
        ListNode* bigtail=bighead;
        ListNode* next=pHead->next;
        while(pHead)
        {
            if(pHead->val<x)
            {
                pHead->next=smalltail->next;
                smalltail->next=pHead;
                smalltail=smalltail->next;
                pHead=next;
                next=next->next;
            }
            else
            {
                pHead->next=bigtail->next;
                bigtail->next=pHead;
                bigtail=bigtail->next;
                pHead=next;
                next=next->next;
            }
        }
        smalltail->next=bighead->next;
        pHead=smallhead->next;
        free(smallhead);
        free(bighead);
        return pHead;
    }
};

🌇7.链表的回文结构

思路：

所谓回文结构，就是左右中心对称。

我们的想法就是先找到链表的中点，然后逆置后面的这个链表，然后顺序对比。

这里分奇偶讨论一下

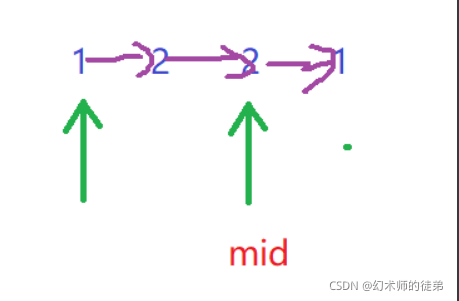
可以观察到，偶数情况下，比较时遍历完后面那个链表就行

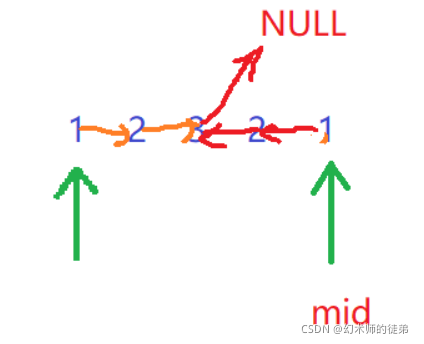
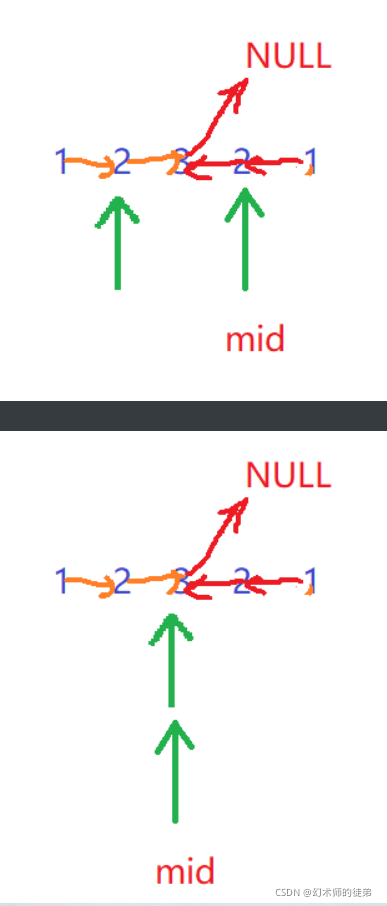
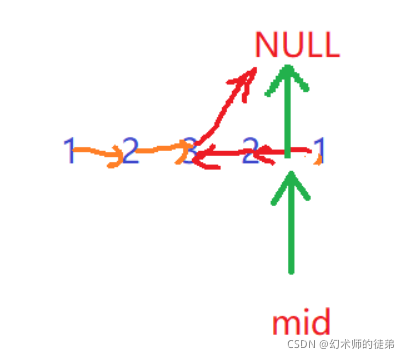
我们要注意，逆置数组的时候我们不会修改2的next是3这个事实，所以遍历的时候也可以一直遍历到结尾。

struct ListNode* findmid(struct ListNode* pHead)
{
    struct ListNode* slow=pHead;
    struct ListNode* fast=pHead;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
    }
    return slow;
}

struct ListNode* reverseList(struct ListNode* head)
{
    if(head!=NULL)
    {
        //p1是p2的前继
        //p2是正要反转的节点的指针
        //p3是p2的后继的指针 为了保证能够迭代
        struct ListNode* p1=NULL;
        struct ListNode* p2=head;
        struct ListNode* p3=p2->next;
        while(p2->next!=NULL)
        {
            p2->next=p1;
            p1=p2;
            p2=p3;
            p3=p3->next;
        }
        p2->next=p1;
        head=p2;
    }
    return head;
}

class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
        struct ListNode* front=A;
        struct ListNode* back1=findmid(A);
        struct ListNode* back=reverseList(back1);
        while(back)
        {
            if(front->val!=back->val)
            {
                return false;
            }
            front=front->next;
            back=back->next;
        }
        return true;
    }
};

🎡8.相交链表

由于链表相交时，结点完全相同（因为地址相同），所以相交的链表绝对是Y型。

思路1.暴力遍历

两个指针遍历所有可能性，一个指针指向一个链表中的一个结点，另一个指针用来遍历另一个链表，如果节点地址相等就是相交 并且这个节点就是交点 时间复杂度O(n^2)。

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    struct ListNode* curA=headA;
    struct ListNode* curB=headB;
    for(curA=headA;curA!=NULL;curA=curA->next)
    {
        for(curB=headB;curB!=NULL;curB=curB->next)
        {
            if(curA==curB)
            {
                return curA;
            }
        }
    }
    return NULL;    
}

思路2：观察发现尾结点相同就是相交，否则就不相交，同时求出两个链表的长度；然后长的先走差距步，然后一起走，直到结点相等，时间复杂度是O(n)

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    struct ListNode* tailA=headA;
    struct ListNode* tailB=headB;
    int lenA=1;
    int lenB=1;
    //只比较尾相不相同就能判断这个链表相不相交
    while(tailA->next)
    {
        lenA++;
        tailA=tailA->next;
    }
    while(tailB->next)
    {
        lenB++;
        tailB=tailB->next;
    }
    if(tailA!=tailB)
    {
        return NULL;
    }
    int gap=abs(lenA-lenB);//绝对值
    struct ListNode* longlist=headA;
    struct ListNode* shortlist=headB;
    if(lenA<lenB)
    {
        shortlist=headA;
        longlist=headB;
    }
    while(gap--)//gap-- 走gap次循环 --gap走gap-1次循环
    {
        longlist=longlist->next;
    }
    while(longlist!=shortlist)
    {
        longlist=longlist->next;
        shortlist=shortlist->next;
    }
    return longlist;
}

🛕9.环形链表的判断

利用物理中的追击相遇问题：

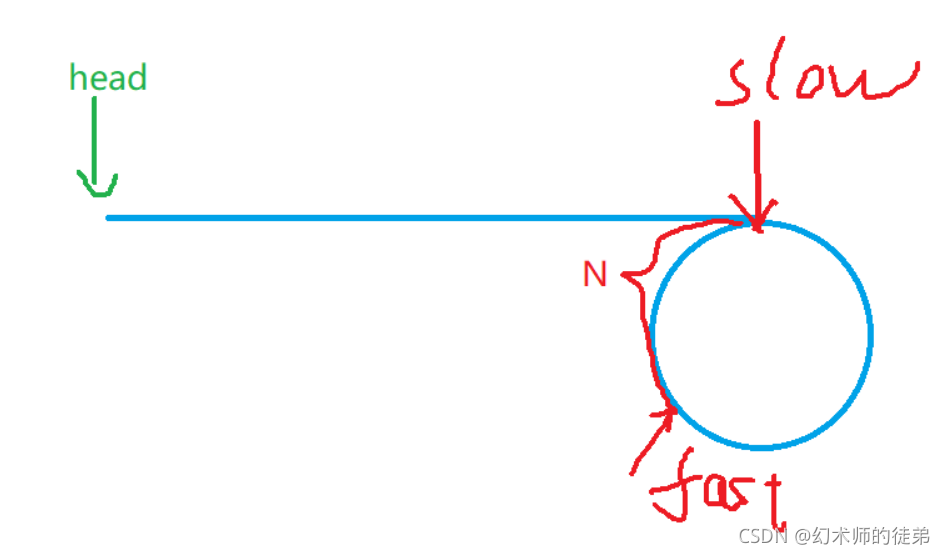
fast指针每次走两步，slow指针每次都一步，如果会相遇，则说明有环，否则fast或者fast->next到了NULL，说明无环。

这里为什么会相遇而不会错过呢，或者说我们为什么要这么设计速度呢？

fast每次走两步，slow每次走一步，fast相对slow的速度是1，当slow入环后，不管fast和slow之间的距离是多少，这个距离肯定是一个整数，每次fast都相对的能追1，所以一定会追到某一步他们俩之间的距离是0了，表明相遇了。

如果我们设计其他的相对速度就不好，比如设计fast每次走3步，slow每次走一步，slow入环，假设fast和slow的距离是N，此后每移动一次，fast和slow的相对距离变化如下：
$$N?2,N?4,N?6,...,0(N是偶数)$$

$$N?2,N?4,...,1,?1(N是奇数)$$

如果是偶数就相遇了，如果是奇数的话，那么相当于fast和slow的距离是C-1
$$C?1,C?3,...,0(C?1是奇数)$$

$$C?1,C?3,...,1,?1(C?1是奇数)$$

然后又按照C-1的距离进行往复，如果N是奇数且C-1是奇数就永远没办法相遇了。

其他的相对速度情况下，都是类似的，相对速度是k的情况下，如果N和C-1 C-2,…C-(k-1)都不是k的倍数，那么也永远不会相遇.

🎃10.环形链表求交点

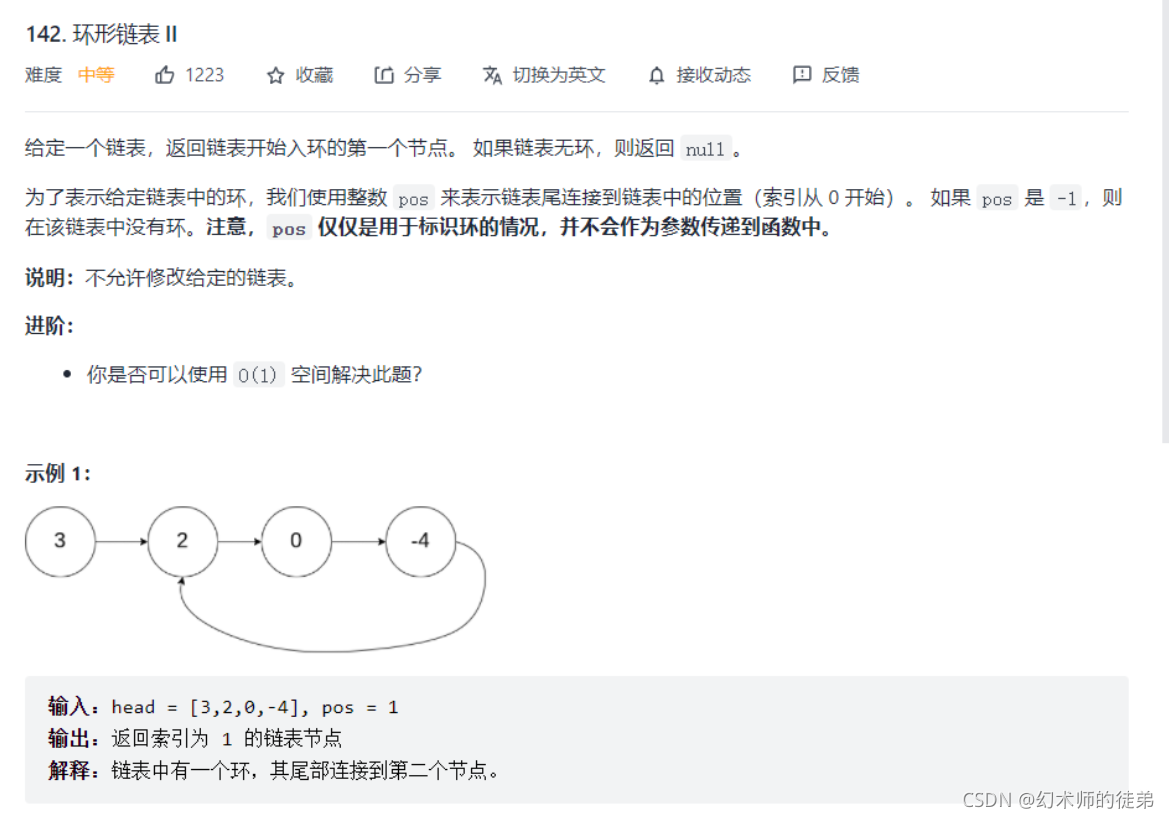
思路1：我们延续之前的思考，当两者相遇时

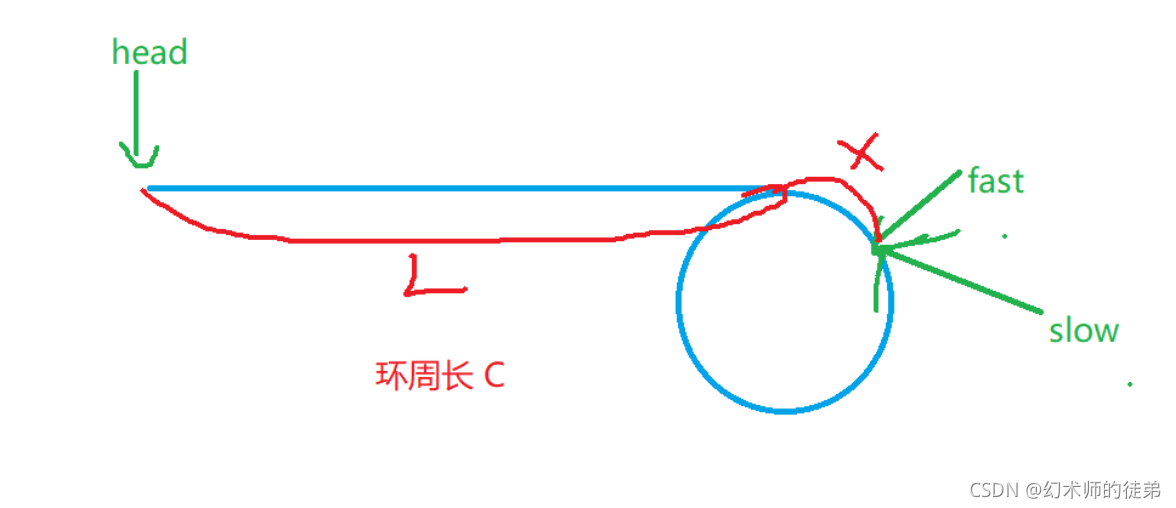
利用fast的速度是slow的两倍，有：
$$(L+X)?2=NC+X+L$$

$$X=NC?L$$

所以即指向相遇位置的指针为meet，头指针和meet同时每次走一步，当走指针走过L步的时候（即到达入环的位置的时候），meet在圆弧中的相对位置是NC，这也就是入环位置，他们会相遇，这个相遇位置就是我们要返回的位置。

struct ListNode *detectCycle(struct ListNode *head) 
{
    //思路一 先判断有没有环 快慢指针法 
    //判断相遇以后根据数学推导让头结点和meet一起走 相遇位置就是开始入环的第一个节点
    struct ListNode* fast=head;
    struct ListNode* slow=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            struct ListNode* meet=slow;
            while(meet!=head)
            {
                meet=meet->next;
                head=head->next;
            }
            return meet;
        }
    }
    return NULL;    
}

思路2：

先用同样的方法判断是否有环，如果有环，那么把相遇点拆开，meet 和meet->next，然后把head到meet这一部分的链表取逆置，然后转化为一个相交链表求交点的问题，注意，题目中不允许我们修改链表，所以我们要找完交点后再把链表还原回去。

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    struct ListNode* tailA=headA;
    struct ListNode* tailB=headB;
    int lenA=1;
    int lenB=1;
    //只比较尾相不相同就能判断这个链表相不相交
    while(tailA->next)
    {
        lenA++;
        tailA=tailA->next;
    }
    while(tailB->next)
    {
        lenB++;
        tailB=tailB->next;
    }
    int gap=abs(lenA-lenB);//绝对值
    struct ListNode* longlist=headA;
    struct ListNode* shortlist=headB;
    if(lenA<lenB)
    {
        shortlist=headA;
        longlist=headB;
    }
    while(gap--)//gap-- 走gap次循环 --gap走gap-1次循环
    {
        longlist=longlist->next;
    }
    while(longlist!=shortlist)
    {
        longlist=longlist->next;
        shortlist=shortlist->next;
    }
    return longlist;
}

struct ListNode *detectCycle(struct ListNode *head) 
{
    //思路二 相遇后 转化为一个相交链表问题
    struct ListNode* fast=head;
    struct ListNode* slow=head;
    struct ListNode* memory=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        {
            //首先 要逆置从head到meet这个点的链表
            //原地逆置法
            struct ListNode* meetnext=slow->next;
            struct ListNode* meet=slow;
            struct ListNode* pre=NULL;
            struct ListNode* next=head->next;
            while(head!=slow)
            {
                head->next=pre;
                pre=head;
                head=next;
                next=next->next;
            }
            slow->next=pre;
            struct ListNode* ret= getIntersectionNode(meet,meetnext);
            //再逆置回去
            struct ListNode* pre1=meetnext;
            struct ListNode* next1=slow->next;
            struct ListNode* cur=slow;
            while(cur->next)
            {
                cur->next=pre1;
                pre1=cur;
                cur=next1;
                next1=next1->next;
            }
            cur->next=pre1;
            return ret;
        }
    }
    return NULL;     
}