1 简介
2009,伊朗的Esmat Rashedi等人基于万有引力定律和粒子间相互作用提出了一种新型的优化算法——引力搜索算法(Gravitational Search Algorithm,GSA)?。?具体原理如下:





2 部分代码
% 万有引力搜索算法
clc,clear,close?all
warning?off
feature?jit?off
N=50; ? ? ? ? ??% 粒子数量(智能个体)
max_it=100; ? ?% 最大迭代次数
ElitistCheck=1;?% ElitistCheck: 算法执行次数选择
Rpower=1; ? ? ??% Rpower: 'R'的次方
min_flag=1; ? ??% 1: 求函数最小值,0:求函数最大值
F_index=1; ? ? ?% 带求解函数选择
[Fbest,Lbest,BestChart,MeanChart]=GSA(F_index,N,max_it,ElitistCheck,min_flag,Rpower);
% 输出:
% Fbest: 最优适应度值.
% Lbest: 最优解向量
% BestChart: 适应度变化值.
% MeanChart: 平均适应度变化值
Fbest, ?% 最优适应度值
Lbest, ?% 最优解
%% 绘制适应度曲线
figure('color',[1,1,1])
plot(BestChart,'linewidth',2),
xlabel('\fontsize{12}\bf Iteration');ylabel('\fontsize{12}\bf 最优适应度值');
legend('\fontsize{10}\bf GSA',1);
grid?on
img?=gcf; ?%获取当前画图的句柄
print(img,?'-dpng',?'-r600',?'./img.png') ? ? ? ??%即可得到对应格式和期望dpi的图像
figure('color',[1,1,1])
plot(MeanChart,'linewidth',2),
xlabel('\fontsize{12}\bf Iteration');ylabel('\fontsize{12}\bf 平均适应度值');
legend('\fontsize{10}\bf GSA',1);
grid?on
img?=gcf; ?%获取当前画图的句柄
print(img,?'-dpng',?'-r600',?'./img1.png') ? ? ? ??%即可得到对应格式和期望dpi的图像
3 仿真结果
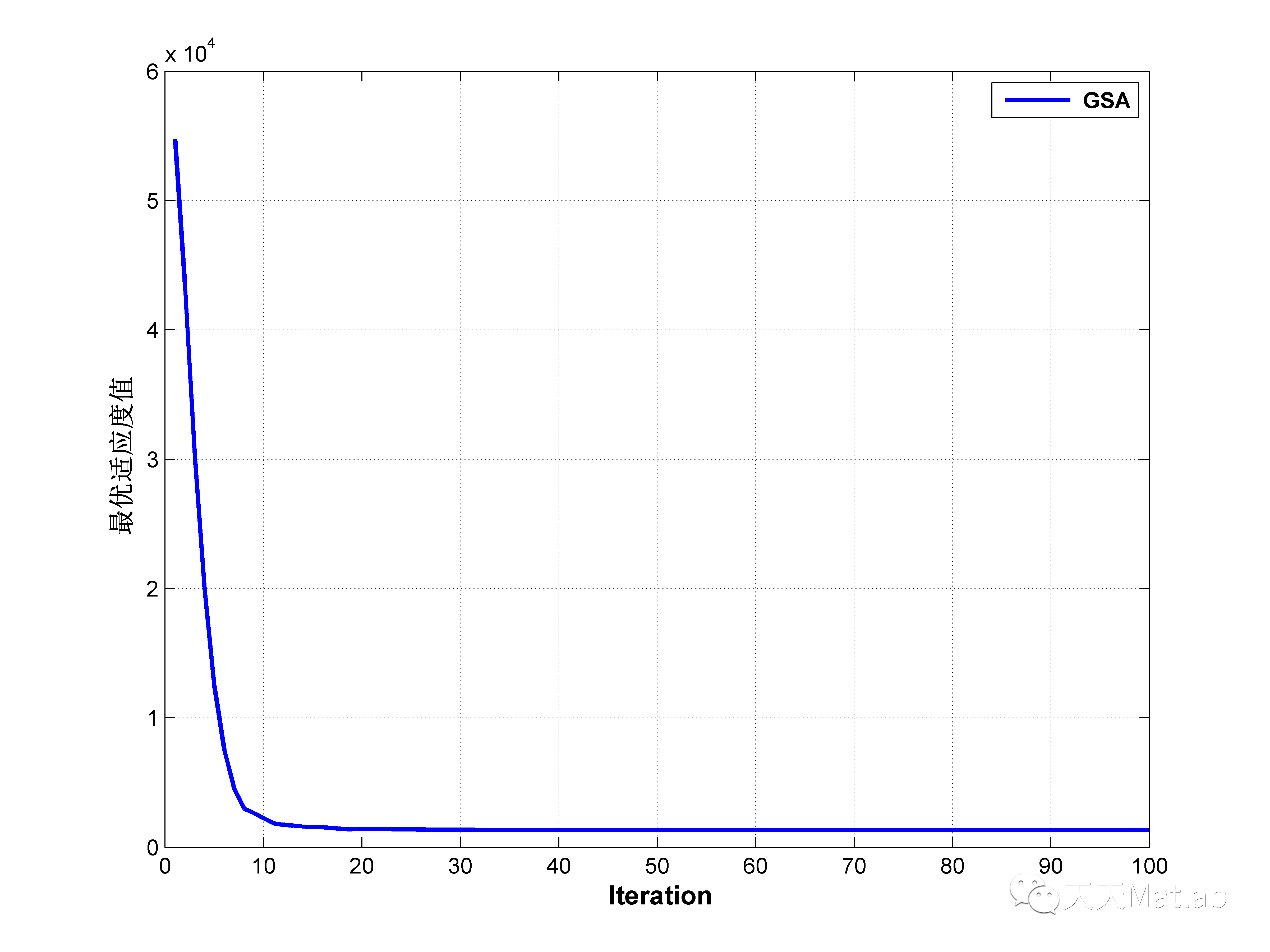
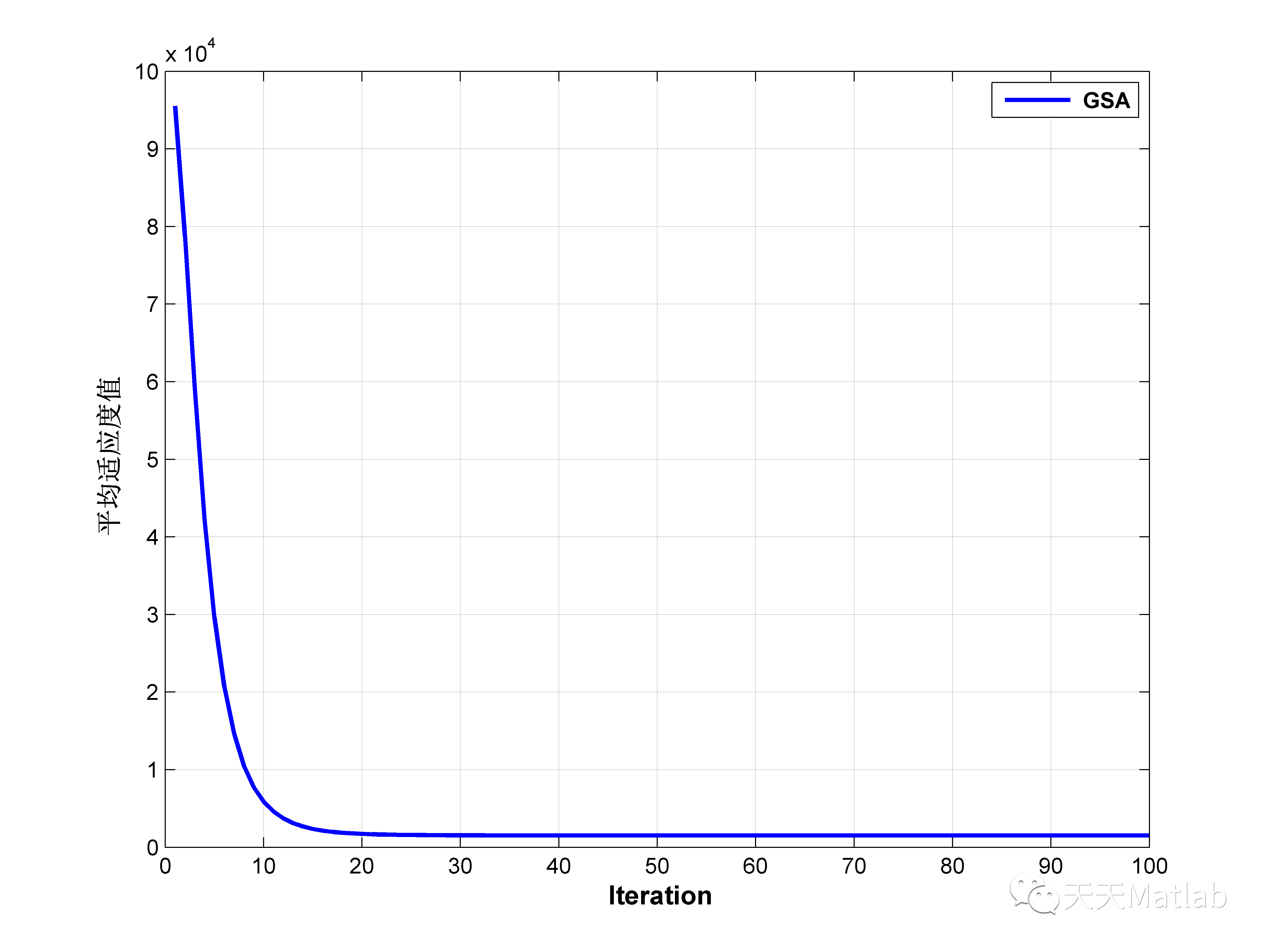
4 参考文献
[1]徐遥, 王士同. 引力搜索算法的改进[J]. 计算机工程与应用, 2011, 47(35):5.
?
