选择排序逻辑:
一趟排序记录最小的数,放到第一个位置
再一趟排序记录记录列表无序区最小的数,放到第二个位置;
算法关键点:有序区和无序区、无序区最小数的位置
为什么叫选择排序
因为这个过程中,我们是不断选出无序区的最小值,所以叫选择排序。
选择排序写法1(较差的写法)
逻辑:先创建一个新的空列表,每次从待排序的列表中拿出最小值,追加到新列表中,最后得到的新列表就是排好序的列表了。
def select_sort_simple(li):
new_li = []
for i in range(len(li)):
min_val = min(li)
new_li.append(min_val)
li.remove(min_val)
return new_li
li = [3, 2, 7, 1, 5, 0, 4, 6, 9, 8]
print(select_sort_simple(li))
由于中间有min和remove函数,这2个的复杂度都是O(n),记为一个O(n)
这里面有2个函数min和remove,是2个O(n^2), 两个记为一个,总体复杂度是O(n^2)
选择排序写法1(较好的写法)
逻辑:
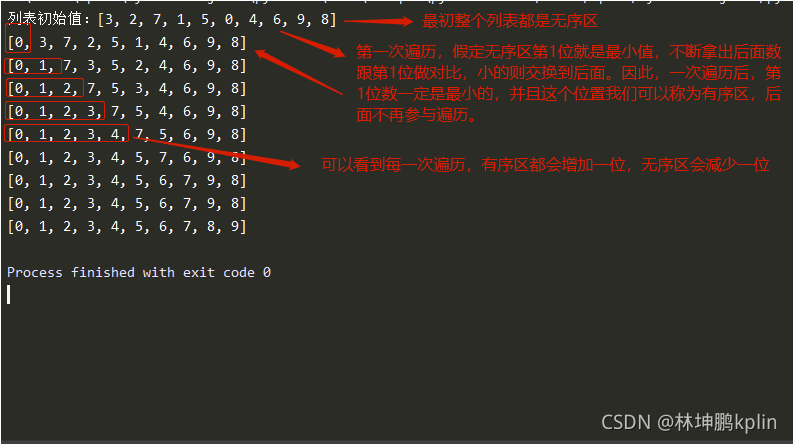
最初整个列表都是无序区,
第一次遍历时,先假定无序区第1位就是最小值,不断拿出后面数跟第1位做对比,小的则交换到后面。
因此,一次遍历后,第1位数一定是最小的,并且这个位置我们可以称为有序区,后面不再参与遍历。
如下图可以看到:每一次遍历,有序区都会增加一位,无序区会减少一位
如果列表有n 个值,则重复这个过程 n-1遍即可。
def select_sort(li):
for i in range(len(li)-1):
min_loc = i
for j in range(i+1, len(li)):
if li[j] < li[min_loc]:
li[j], li[min_loc] = li[min_loc], li[j]
print(li)
return li
li = [3, 2, 7, 1, 5, 0, 4, 6, 9, 8]
select_sort(li)
总体复杂度是O(n^2)