[数据结构与算法] 2021-10-23_LeetCode第2题

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 2021-10-23_LeetCode第2题_两数相加 -> 正文阅读

[数据结构与算法]2021-10-23_LeetCode第2题_两数相加

题目要求：
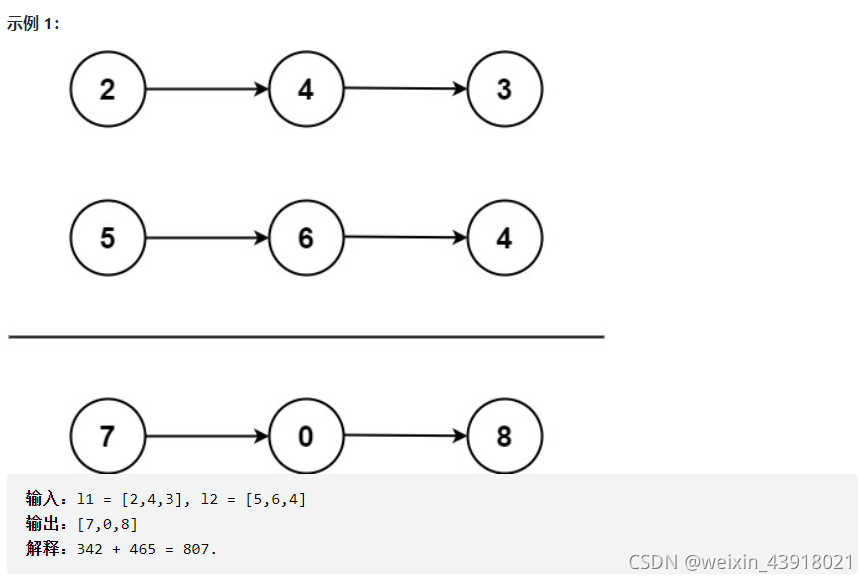
给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
在这里插入图片描述
函数原型如下：

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2);

解题思路1：
本题就是使用链表实现一个加法运算，既然是加法运算，按照最基本的运算法则，仅需要从低位到高位，依次相加求和即可。
从低位到高位，依次相加求和 这句话看似简单，但是在设计程序时，需要考虑2件事：
1）数字1和数字2的位数是否相同，假如加数1和加数2位数不相同，应该如何处理；
2）相加过程中如果产生进位如何处理；
于是有了上述大体思路，展开了程序设计，整体逻辑如下：
1）判断边界条件，如果链表1、链表2有为空的，直接返回另一个链表即可；
2）如果都不为空，则开始计算加和，有进位，设置进位变量置1，没有进位置0，将求和结果对10取余后，添加进入链表，并生成下一个链表节点；
3）判断l1，l2两个链表是否出现空，如果出现，则按照以下方法处理：若l1、l2同时为空，则判断有无进位，无进位，运算结束，有进位则需要持续加下去；若l1不为空，则将l1剩下的数位加和完毕；若l2不为空，则将l2剩下的数位加和完毕；
代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
    public:
     ListNode* addTwoNumbers(ListNode* l1, ListNode* l2)
    {
        ListNode *pResult = new ListNode(0,nullptr);
        ListNode *pResultCurrent = pResult;
        ListNode *pResultLast = pResult;
        ListNode* pl1 = l1;
        ListNode* pl2 = l2;
        int set_flag = 0;
        int sum = 0;
        if((pl1->val == 0 && pl1->next == nullptr)|| (pl1 == nullptr))
        {
            return l2;
        }
        else if((pl2->val == 0 && pl2->next == nullptr )|| (pl2 == nullptr))
        {
            return l1;
        }
        else
        {
            /**/
            while((pl1 != nullptr) && (pl2 != nullptr))
            {
                sum = pl1->val + pl2->val + set_flag;
                if(sum >= 10 )
                {
                set_flag = 1;
                sum = sum - 10;
                }
                else
                {
                    set_flag = 0;
                }
                pResultCurrent->val = sum;
                pResultCurrent->next = new ListNode();
                pResultLast = pResultCurrent; // save current point
                pResultCurrent = pResultCurrent->next;//point to new ListNode
                pl1 = pl1->next;
                pl2 = pl2->next;

            }
            if(pl1 == nullptr && pl2 == nullptr)
            {
                if(set_flag == 0)
                {
                    pResultLast->next = nullptr;
                }
                else if(set_flag == 1)
                {
                    pResultCurrent->val  = set_flag;
                    pResultCurrent->next  = nullptr;
                }
                return  pResult;
            }
            else if(pl1 != nullptr)
            {
                while(pl1 != nullptr)
                {
                    int sum = pl1->val  + set_flag;
                    if(sum >= 10 )
                    {
                        set_flag = 1;
                        sum = sum - 10;
                    }
                    else
                    {
                        set_flag = 0;
                    }
                    pResultCurrent->val = sum;
                    pResultCurrent->next = new ListNode();
                    pResultLast = pResultCurrent; // save current point
                    pResultCurrent = pResultCurrent->next;//point to new ListNode
                    pl1 = pl1->next;
                }

                if(set_flag == 0)
                {
                    pResultLast->next = nullptr;
                }
                else if(set_flag == 1)
                {
                    pResultCurrent->val  = set_flag;
                    pResultCurrent->next  = nullptr;
                }
                return  pResult;
            }
            else if(pl2 != nullptr)
            {
                while(pl2 != nullptr)
                {

                    int sum = pl2->val  + set_flag;
                    if(sum >= 10 )
                    {
                        set_flag = 1;
                        sum = sum - 10;
                    }
                    else
                    {
                        set_flag = 0;
                    }
                    pResultCurrent->val = sum;
                    pResultCurrent->next = new ListNode();
                    pResultLast = pResultCurrent; // save current point
                    pResultCurrent = pResultCurrent->next;//point to new ListNode
                    pl2 = pl2->next;
                }

                if(set_flag == 0)
                {
                    pResultLast->next = nullptr;
                }
                else if(set_flag == 1)
                {
                    pResultCurrent->val  = set_flag;
                    pResultCurrent->next  = nullptr;
                }
                return  pResult;
            }
        }
        return pResult;
    }
};

执行结果如下：
1568 / 1568 个通过测试用例
状态：通过
执行用时: 36 ms
内存消耗: 69.5 MB
运行速度：击败了33%的用户
由于链表很久不写了，整个程序设计思路虽然比较清晰，但是并没有充分的归并判断条件，不太复杂的功能，用了100多行代码才实现，加之运行效率不高，从这个角度上来说，这段代码是比较失败的。
看了他人的代码（简洁明了，一针见血），更印证了我的想法，于是在读懂别人的代码上，有了解题思路2。

解题思路2：
上边的解题思路，将进位、加数位数等几个问题分别进行了考虑，考虑了较多的条件，而并没有一下抓住问题的本质。其实加数问题的核心，就是要确定“我们在什么条件下要继续算下去？”这个简单而又朴素的问题，而回答也非常简单：没加到最高位，我们要继续算，有进位了，我们也要继续算；翻译成更贴近于代码的话，就是链表1不空、链表2不空、进位不为0，只要三者满足其一，我们就需要继续计算。
废话不多说，直接上代码吧！

 ListNode* addTwoNumbers(ListNode* l1, ListNode* l2)
{
    ListNode *pResult = new ListNode(0,nullptr);
    ListNode *pCur = pResult;
    int set_flag = 0;
    while(l1 !=nullptr || l2!=nullptr || set_flag !=0)
    {
        int l1val = 0;
        int l2val = 0;
        if(l1 != nullptr )
        {
            l1val = l1->val;
        }
        if(l2 != nullptr)
        {
            l2val = l2->val;
        }
        int sum = l1val + l2val + set_flag ;
        set_flag = sum /10;
        pCur->next = new ListNode(sum %10);
        pCur = pCur->next;
        if(l1 != nullptr) l1 = l1->next;
        if(l2 != nullptr) l2 = l2->next;
    }
    return pResult->next ;

}

运行结果如下：
1568 / 1568 个通过测试用例
状态：通过
执行用时: 32 ms
内存消耗: 69.5 MB
运行速度：击败了33%的用户
代码清晰明了，实现简单，一下抓住问题的本质，看了直呼过瘾。

解题思路3：
提升效率实在解题思路1的代码上优化的：
1）考虑加和运算时，如果数位用完了，进位为0，可考虑直接将结果链表指向未进行完的加和运算的数字的相应数位，可在一定程度上提高程序运行效率和内存节省一部分内存空间；
2）并且由于在解题思路1中，代码判断了较多边界情况，在测试案例比较多时，会极大影响效率，根据上述情况，更改代码如下：

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2)
{
    ListNode *pResult = new ListNode(0,nullptr);
    ListNode *pResultCurrent = pResult;
    ListNode *pResultLast = pResult;
    ListNode* pl1 = l1;
    ListNode* pl2 = l2;
    int set_flag = 0;
    int sum = 0;
    while((pl1 != nullptr) && (pl2 != nullptr))
    {
        sum = pl1->val + pl2->val + set_flag;
        if(sum >= 10 )
        {
        set_flag = 1;
        sum = sum - 10;
        }
        else
        {
            set_flag = 0;
        }
        pResultCurrent->val = sum;
        pResultCurrent->next = new ListNode();
        pResultLast = pResultCurrent; // save current point
        pResultCurrent = pResultCurrent->next;//point to new ListNode
        pl1 = pl1->next;
        pl2 = pl2->next;

    }
    if(pl1 == nullptr && pl2 == nullptr)
    {
        if(set_flag == 0)
        {
            pResultLast->next = nullptr;
        }
        else if(set_flag == 1)
        {
            pResultCurrent->val  = set_flag;
            pResultCurrent->next  = nullptr;
        }
        return  pResult;
    }
    else if(pl1 != nullptr)
    {
        while(pl1 != nullptr)
        {
            if(set_flag == 0)
            {
                pResultLast->next = pl1;
                return pResult;
            }
            int sum = pl1->val  + set_flag;
            if(sum >= 10 )
            {
                set_flag = 1;
                sum = sum - 10;
            }
            else
            {
                set_flag = 0;
            }
            pResultCurrent->val = sum;
            pResultCurrent->next = new ListNode();
            pResultLast = pResultCurrent; // save current point
            pResultCurrent = pResultCurrent->next;//point to new ListNode
            pl1 = pl1->next;
        }

        if(set_flag == 0)
        {
            pResultLast->next = nullptr;
        }
        else if(set_flag == 1)
        {
            pResultCurrent->val  = set_flag;
            pResultCurrent->next  = nullptr;
        }
        return  pResult;
    }
    else if(pl2 != nullptr)
    {
        while(pl2 != nullptr)
        {
            if(set_flag == 0)
            {
                pResultLast->next = pl2;
                return pResult;
            }
            int sum = pl2->val  + set_flag;
            if(sum >= 10 )
            {
                set_flag = 1;
                sum = sum - 10;
            }
            else
            {
                set_flag = 0;
            }
            pResultCurrent->val = sum;
            pResultCurrent->next = new ListNode();
            pResultLast = pResultCurrent; // save current point
            pResultCurrent = pResultCurrent->next;//point to new ListNode
            pl2 = pl2->next;
        }

        if(set_flag == 0)
        {
            pResultLast->next = nullptr;
        }
        else if(set_flag == 1)
        {
            pResultCurrent->val  = set_flag;
            pResultCurrent->next  = nullptr;
        }
        return  pResult;
    }
    return pResult;
}