[数据结构与算法]LeetCode 杨辉三角

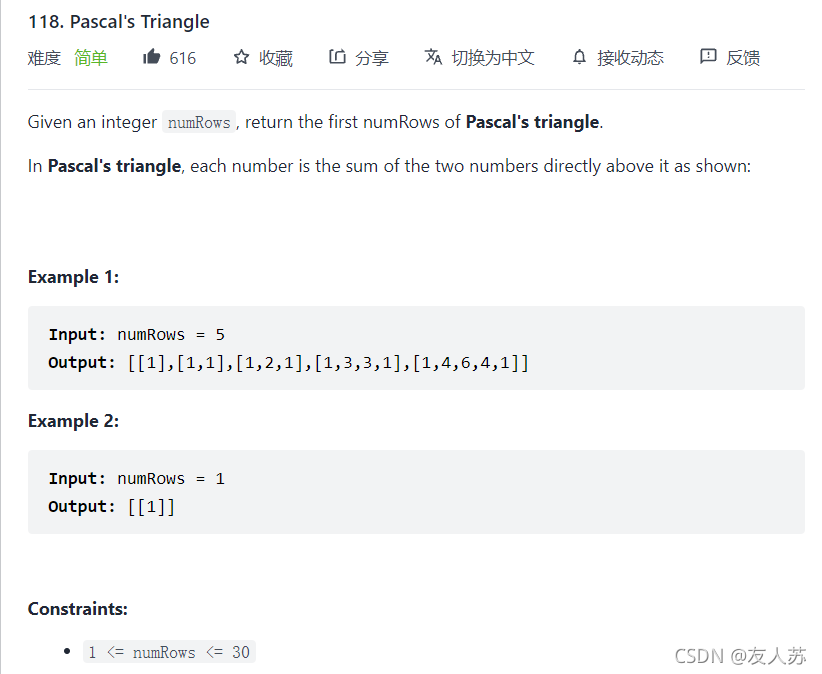
杨辉三角是一个比较经典的动态规划，它的状态方程也很简单，当j == 0 || i== j时，dp[ i ][ j ] = 1，其他情况则是 dp[i][j] = dp[i - 1][j -1] + dp[i - 1][ j ]。

代码如下：

int** generate(int numRows, int* returnSize, int** returnColumnSizes){
	//用malloc申请一块连续的空间，该空间内的元素都是指针类型，所以ret因定义为一个二级指针
    int** ret = (int*)malloc(sizeof(int*) * numRows);
    //返回数组的行
    *returnSize = numRows;
    //返回数组的列
    *returnColumnSizes =(int*) malloc(sizeof(int) * numRows);
    for(int i = 0; i < numRows; i++){
    	//ret[i]是一个一级级指针，用malloc申请一块长的为i+1的整型空间，并将其首地址返回给ret[i]
        ret[i] = malloc(sizeof(int) * (i + 1));
        (*returnColumnSizes)[i] = i + 1;
        ret[i][0] = ret[i][i] = 1;
        for (int j = 1; j < i; ++j) {
        	//状态方程
            ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
        }
    }
    return ret;
}

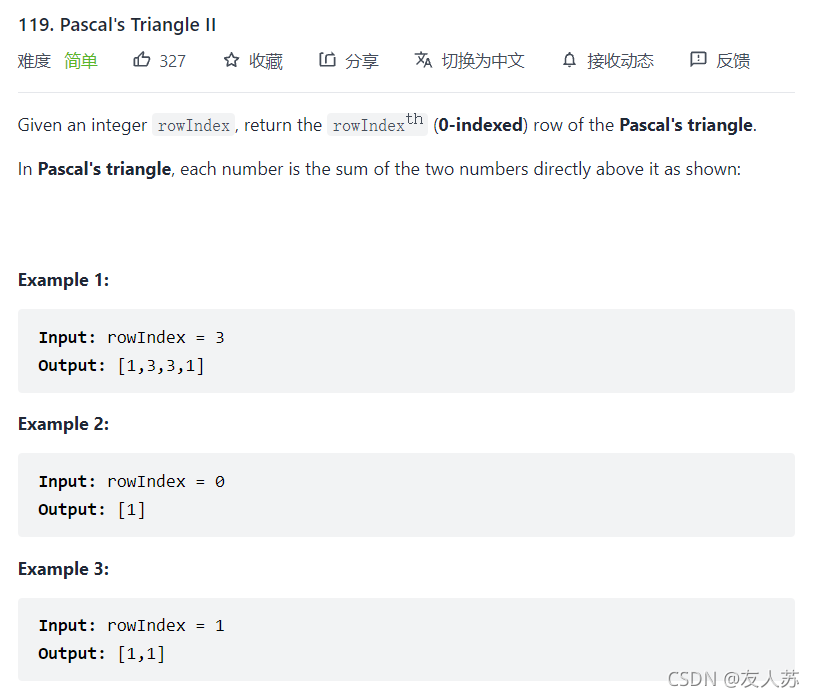
这道题与上面不一样的是，上面那道题是将前rowIndex行包括rowIndex这行的数据都打印出来，而这道题只需打印下标为rowIndex这一行的数据。所以我们只需将dp[rowIndex]返回即可。

int* getRow(int rowIndex, int* returnSize){
    *returnSize = rowIndex + 1;
    int** dp = (int**)malloc(sizeof(int*) * (rowIndex + 1));
    for(int i = 0; i <= rowIndex; i++){
        dp[i] = (int*)malloc(sizeof(int) * (i + 1));
        for(int j = 0; j <= i; j++){
            if(j == 0 || j == i){
                dp[i][j] = 1;
            }
            else{
                dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
            }
        }
    }
    return dp[rowIndex];

}