[数据结构与算法]红黑树的数据结构

红黑树

• 红黑树，是二叉搜索树的一种，也是一种特化的二叉平衡树，它不追求完全平衡，追求的是一种大致平衡，以达到在 插入、查找、删除 的时间复杂度最好情况和最坏情况都维持在 $O(logN)$；
• 红黑树的特殊在于，进行查找和删除操作时，可以进行 自平衡；
• 红黑树的生长是自底向上的；

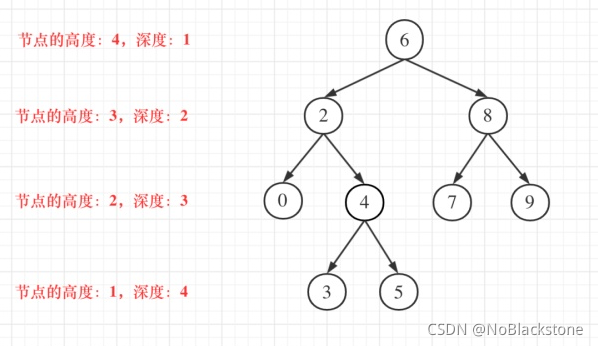
• 二叉树某节点的深度：指树的根节点到该节点的最长简单路径的边数（或节点数）；

• 二叉树某节点的高度：指该节点到叶子节点的最长简单路径的边数（或节点数）；

• 下图按节点数结算：

  

• 二叉平衡树：

  • 可以是空树；
  • 任何一个节点的左右子树都是平衡树，且高度之差的绝对值不超过1；

• 二叉搜索树：
  左子树的所有节点都比父节点小，右子树的所有结点都比父结点大；

• AVL树，即自平衡二叉搜索树：平衡树和搜索树的结合；

定义和性质

• 红黑树是一种含有红黑节点并能自平衡的二叉搜索树，满足一下性质：
  • 性质1：每个节点都可以为红色节点或黑色节点；
  • 性质2：根节点一定是黑色节点；
  • 性质3：每个叶子节点（nullptr）都是黑色节点（叶子节点是空节点，可以不显示出来）；
  • 性质4：每个红色节点的两个子节点一定都是黑色节点；
  • 性质5：任意一节点到每个叶子节点的路径都包含数量相同的黑色节点；
• 推论1：如果一个节点存在一个黑色子节点，那么该节点肯定有两个子节点；
• 推论2：一个黑色节点的两个子节点不一定都是红色节点；
• 推论3：不能同时存在两个直接相连的红色节点；
• 黑色完美平衡：左右子树的的黑色节点层数是相等的，即任意一节点到每个叶子节点的路径都包含数量相同的黑色节点；
• 自平衡的操作：
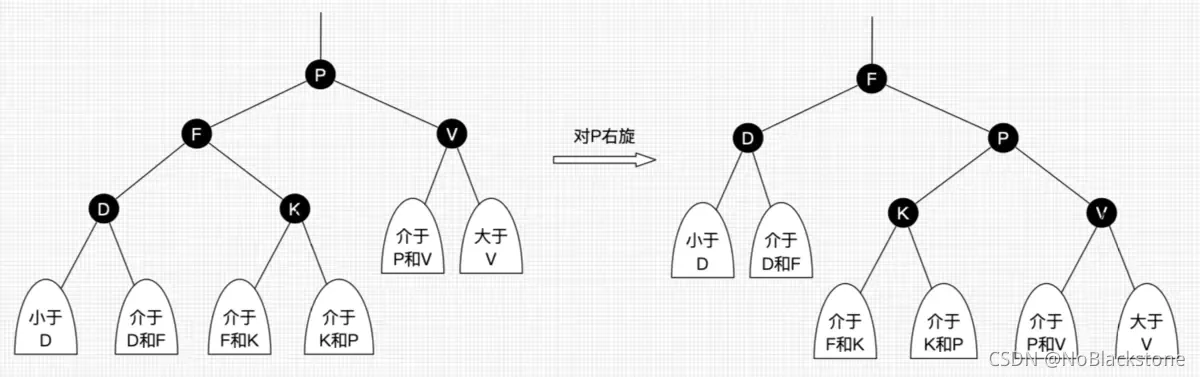
  • 左旋：以某个节点 P 作为支点（旋转节点），其右子节点 V 变为旋转节点 P 的父节点，其右子节点 V 的左子节点 R 变为旋转节点 P 的右子节点，其右子节点 V 的右子节点 X 保持不变；
  • 右旋：以某个节点 P 作为支点（旋转节点），其左子节点 F 变为旋转节点 P 的父节点，其左子节点 F 的右子节点 K 变为旋转节点 P 的左子节点，其左子节点 F 的左子节点 D 保持不变；
  • 变色：节点的颜色由红转黑、或由黑转红；

查找

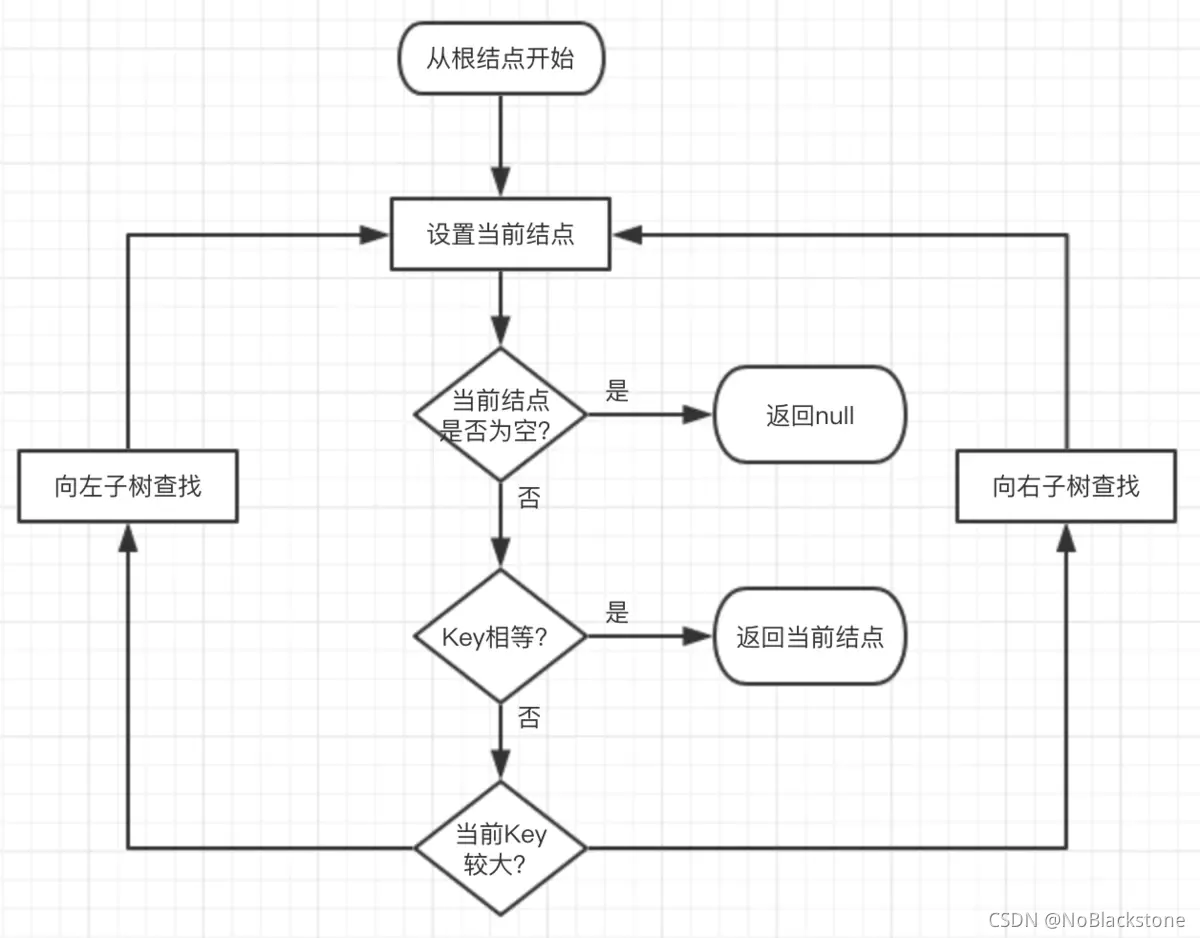
• 红黑树是一棵二叉平衡树，查找方式与正常的二叉平衡树一样：
  • 1、根节点开始查找，把根节点设置为当前节点；
  • 2、若当前节点为空，返回null；
  • 3、若当前节点不为空，判断目标值与当前节点的 value；
  • 4、若相等，则返回当前的节点；
  • 5、若大于，则将当前节点的右子节点设置为当前节点，并重复步骤2；
  • 6、若小于，则将当前节点的左子节点设置为当前节点，并重复步骤2；

• 由于红黑树总是保持黑色完美平衡，所有查找的最坏时间复杂度为 $O(2lgN)$；

插入

• 插入操作包括两部分工作：查找插入的位置，和插入后的自平衡；

• 插入节点的查找：

  • 1、从根节点开始查找；
  • 2、若根节点为空，那么插入节点为根节点，结束；
  • 3、若根节点不为空，将根节点作为当前节点；
  • 4、若当前节点为 nullptr，此为插入节点，结束；
  • 5、若当前节点的 value 等于查找值，那么当前节点为插入节点，更新节点的值，结束；
  • 6、若当前节点的 value 大于查找值，将当前节点的左子节点设置为当前节点，重复步骤4；
  • 7、若当前节点的 value 小于查找值，将当前节点的右子节点设置为当前节点，重复步骤4；

• 插入位置找到后，将插入节点放入正确位置即可；插入节点的颜色，默认为红色；

除了2、插入情景，所有插入操作都是在叶子节点上进行的

1、红黑树为空树

直接将插入节点作为根节点，根据性质2，根节点需为黑色节点，给插入节点设为黑色；

• 处理：
  • 将插入节点作为根节点；
  • 并将节点设置为黑色节点；

2、插入节点的位置存在节点

插入前红黑树已经是平衡的，将插入节点设置为替换节点的颜色，并更新节点的元素值即可；

• 处理：
  • 将插入节点颜色设置为替换节点的颜色；
  • 更新当前节点为插入节点；

3、插入节点的父节点为黑色节点

插入的节点默认是红色节点，并不会影响红黑树的黑平衡；

• 处理：
  • 直接插入

4、插入节点的父节点为红色节点

如果插入的父节点为红色节点，那么该父节点不会是根节点，故插入节点总是存在祖父节点；因为插入结点和父结点都为红色结点，违反推论3，故需自平衡；

4.1、叔叔节点存在 且为红色节点

4.1.1、祖父节点不为根节点

因为插入节点与父节点都是红色节点，故违反了推论3；简单的做法是将黑红红 换成 红黑红，同时将叔叔节点设置为黑色节点；

• 处理：
  • 将 父节点和 叔叔节点设置为黑色；
  • 将 祖父节点设置为红色；
  • 将 祖父节点设为当前的插入节点；

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-STACpNRH-1635141279872)(picture/07.png)]

• 注意：我们在这里将祖父节点 pp 设为 红色节点；
  • 若 pp 节点的父节点是黑色节点，则无需做任何处理；
  • 若 pp 节点的父节点是红色节点，则违反推论3；在此，要将祖父节点 pp 当作新的插入节点，继续做插入操作的自平衡，直到平衡为止；

4.1.2、祖父节点为根节点

若刚好祖父节点 pp 为根节点，将根节点设为红色节点，违反了性质2；此时红黑结构应该由 黑红红 变为 黑黑红；

而从根节点到叶子节点的路径中，黑色节点数增加，这也是唯一一种会增加红黑树的黑色节点层数的插入情景；

同时，这里可以了解到：红黑树的生长是自底向上的；

• 处理：
  • 将父节点和叔叔节点设为黑色节点；

4.2、叔叔节点不存在 或为叶子节点

• 叔叔节点如果不是红色节点，则必然是叶子节点 nullptr；因为如果叔叔节点为黑色节点，而父节点为红色节点，则父结点必然有两个黑色子结点，来维持树的黑平衡，则与插入节点的位置冲突，因为该父节点此时明显没有空余子节点位置；

4.2.1、并且插入节点的父节点 是祖父节点的左子节点

4.2.1.1、插入节点为父节点的左子节点

• 处理：
  • 将 父节点设为黑色；
  • 将 祖父节点设为红色；
  • 对 祖父节点进行右旋；

4.2.1.2、插入节点为父节点的右子节点

• 可以将它转换为 4.2.1.1的插入情景；

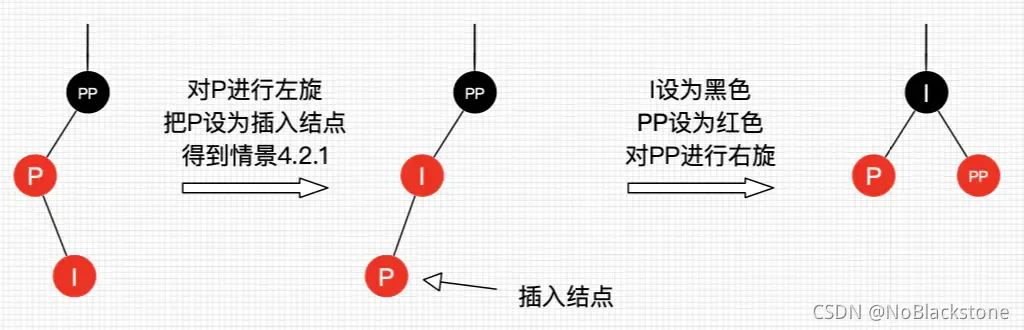
• 处理：
  • 对 父节点进行左旋；
  • 把 父节点设置为插入节点，得到 4.2.1.1的插入情景；
  • 进行 4.2.1.1插入情景的处理；

4.2.2、并且插入节点的父节点 是祖父节点的右子节点

• 情况类似 4.2.1的插入情景，只是方向反转；

4.2.2.1、插入节点为父节点的右子节点

• 处理：
  • 将 父节点设为黑色；
  • 将 祖父节点设为红色；
  • 对 祖父节点进行左旋；

4.2.2.2、插入节点为父节点的左子节点

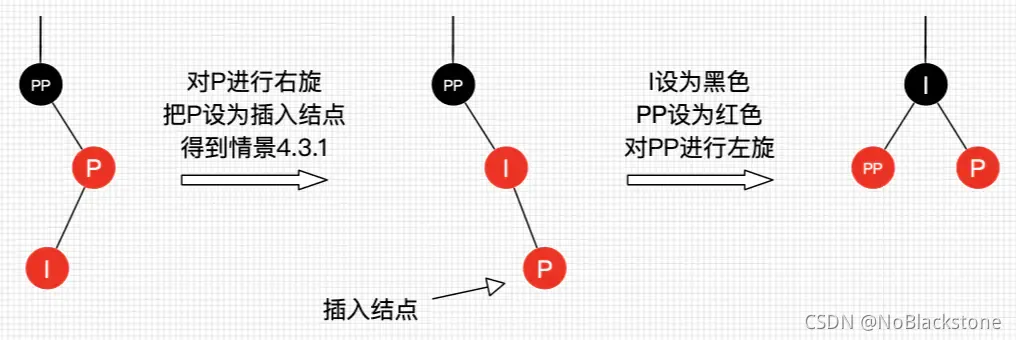
• 处理：
  • 对 父节点进行右旋；
  • 把 父节点设置为插入节点，得到 4.2.2.1的插入情景；
  • 进行 4.2.2.1插入情景的处理；

删除

• 红黑树的操作包括两部分：查找目标节点 和 删除后自平衡；
  • 查找目标点时，若不存在则忽略本次操作；若存在则删除后作自平衡处理；
  • 删除节点后，需要找一个替代节点去替换删除节点的位置，若删除节点没有子节点，则不需要替换；
• 二叉树删除节点对应的替代节点有三种情景：
  • 情景1：若删除节点无子节点，直接删除；
  • 情景2：若删除节点只有一个子节点，用子节点替换删除节点；
  • 情景3：若删除节点有两个子节点，用后继节点（大于删除节点的最小节点）替换删除节点；
    • 后继节点，即删除节点的右子树的最左节点；前继节点，即删除节点的左子树的最右节点，两种节点都可以做替代节点，习惯上使用后继节点，后面也将使用后继节点；
    • 把二叉树所有节点投射在 X 轴上，所有节点都是从左到右排好序的，所有目标节点的前后节点就是对应的前继节点和后继节点；

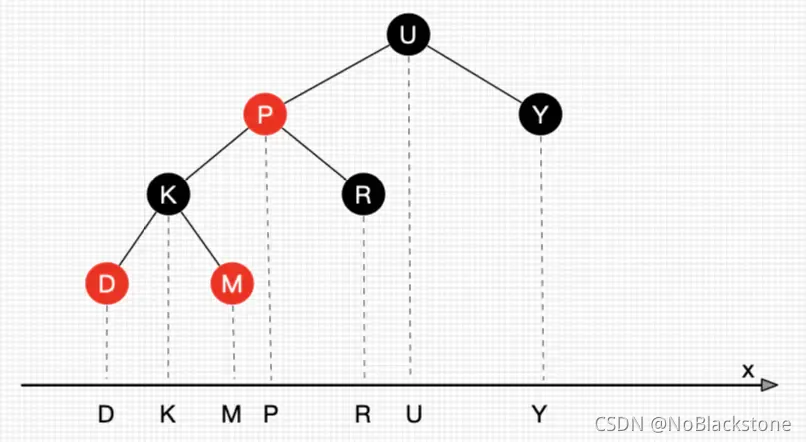
• 一个重要的思路：删除节点被替换后，在不考虑节点的键值情况下，对于树的节点位置来说，可以认为删除的是替代节点的位置；
  

  根据这种思路，上述三种删除情景可以相互转换，并最后都可以转换为删除情景1；

  • **删除情景2的转换：**删除节点用其唯一的子节点进行替换，子节点替换删除节点后，可以认为删除的是子节点；此时，若替代节点存在两个子节点，就相当于转换为删除情景3，一直自顶向下进行转换，总是能转换为删除情景1（而对于红黑树而言，根据推论1，只存在一个子节点的节点肯定在数末）
  • 删除情景3的转换：删除节点的替代节点 为其后继节点（后继节点不存在左子节点），可以暂时认识删除的是后继节点，如果后继节点存在右子节点，那么相当于转换为删除情景2，否则转换为删除情景1；

• 综上所述，删除操作删除的节点位置，可以看作替代节点的位置，而替代节点最后总是在树末，这个结论可以使得删除红黑树的情景少了很多：
  

• 下面将具体讨论红黑树的删除操作的所有情景：

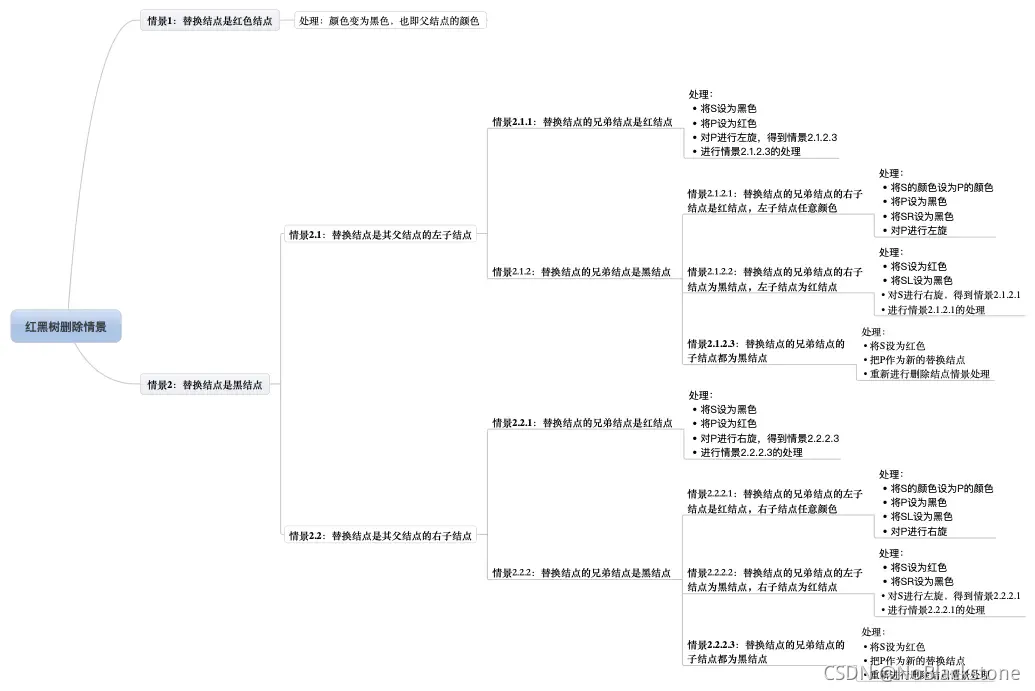
• 灰色节点表示它可以是红色节点 或是黑色节点；R 是即将被替换到删除节点的位置的替代节点，在进行删除操作前，它还在原来所在位置参与树的自平衡，平衡完成后，再替换到删除节点的位置，才算删除完成；

下面的操作最后都需要替代节点替换到删除节点的位置上，如果替换后不能黑平衡，则先不进行替换，需要继续处理替代节点，直到黑平衡为止

1、替换节点为红色节点

• 我们将替代节点替换到删除节点时，由于替代节点是红色节点，替代节点位置的红色节点消失也不会影响红黑树的完美黑平衡，只要把替代节点的颜色设为删除节点的颜色即可重新平衡；
• 处理：
  • 将替代节点设为删除节点的颜色；

2、替代节点为黑色节点

2.1、替代节点 为其父节点的左子节点

2.1.1、替代节点的兄弟节点是红色节点

• 若替代节点的兄弟节点是红色节点，根据性质4，兄弟节点的父节点和子节点肯定是黑色节点；先将父节点设为红色节点，兄弟节点设为黑色节点，然后以父节点为旋转节点进行左旋，转换为新的删除情景，并进行该删除情景的操作（此时的替代节点并没有改变，仍然是 R）；
• 处理：
  • 将 兄弟节点的颜色和 父节点的颜色进行对调；
  • 对 父节点进行左旋，得到新的删除情景；
  • 根据替代节点的新情况，使用对应删除情景的处理；

2.1.2、替代节点的兄弟节点是黑色节点

• 当兄弟节点为黑色节点时，其父节点和子节点的具体颜色无法确定；

2.1.2.1、替换节点的兄弟节点的右子节点是红色节点，左子节点任意

• 在此情景中，即将删除的左子树是一个黑色节点，事后左子树的黑色节点会少了一个，然后右子树有红色节点，那么可以向右子树“借”一个红色节点；
• 处理：
  • 将 兄弟节点的颜色和 父节点的颜色对调；
  • 将 兄弟节点的右子节点设为黑色；
  • 对父节点进行左旋；

• 注意，此时上图的结果看起来不满足红黑树性质；但是它是满足的，因为替代节点是即将要替换的，它要产于树的自平衡，平衡后再替换到删除节点的位置，所以替代节点最终是可以看出被删除的；
• 上图是考虑到第一次替换和自底向上的两个情况：
  • 只考虑第一次替换的情况，根据推论1，当节点有一个黑色子节点时，必然会有另外一个黑色子节点；此时替代节点将会被删除，故此节点 P 只会有一个节点，故节点 SL 只能是红色节点 或是叶子节点 nullptr；
  • 如果是自底向上处理的情况，每棵树都保持平衡状态，最终整棵树一定是平衡的；
  • 后续的情景同理，将不再累赘；

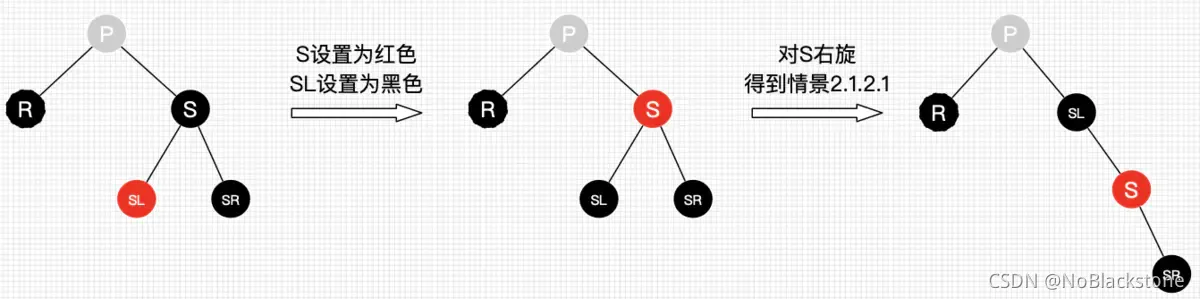
2.1.2.2、替代节点的兄弟节点的右子节点为黑色节点，左子节点为红色节点

• 兄弟节点所在子树有红色节点，可以向兄弟子树“借”红色节点，可以转换为 新的删除情景；
• 处理：
  • 将 兄弟节点的颜色和 其左子节点的颜色对调；
  • 对 兄弟节点进行右旋，得到 新的删除情景；
  • 根据替代节点的新情况，使用对应删除情景的处理；

2.1.2.3、替代节点的兄弟节点的子节点都为黑色节点

• 此情景的兄弟子树没有红色节点可以“借“，只能向上”借“；此处将兄弟节点设为红色节点，将父节点作为替代节点，自底向上处理，去找父节点的兄弟节点；兄弟节点设为红色的理由，是为了保持父节点所在的子树平衡（原替代节点　Ｒ　即将删除，少了一个黑色节点，子树也需要少一个），当然后续的操作交给父辈处理；保证每个子树的平衡，最终整棵树都将平衡；
• 处理：
  • 将 兄弟节点设为红色节点；
  • 将 父节点作为新的替代节点；
  • 根据新的替代节点使用对应的删除情景的处理；

2.2、替代节点是其父节点的右子节点

• 右边的操作是方向相反的；

2.2.1、替代节点的兄弟节点是红色节点

• 处理：
  • 将 兄弟节点的颜色和 父节点的颜色对调；
  • 对 父节点进行右旋，得到 新的删除情景；
  • 根据替代节点的新情况，使用对应删除情景的处理；

2.2.2、替代节点的兄弟节点是黑色节点

2.2.2.1、替代节点的兄弟节点的左子节点是红色，右子节点任意

• 处理：
  • 将 兄弟节点的颜色和 父节点的颜色对调；
  • 将 兄弟节点的左子节点设为黑色；
  • 对 父节点进行右旋；

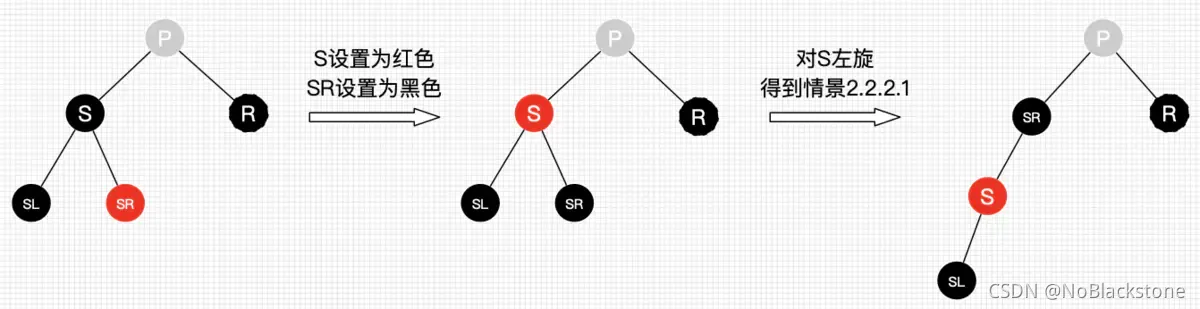
2.2.2.2、替代节点的兄弟节点的左子节点为黑色节点，右子节点为红色节点

• 处理：
  • 将 兄弟节点设为红色；
  • 将 兄弟节点的右子节点设为黑色；
  • 对 兄弟节点进行左旋，得到 新的删除情景；
  • 根据替代节点的新情况，使用对应删除情景的处理；

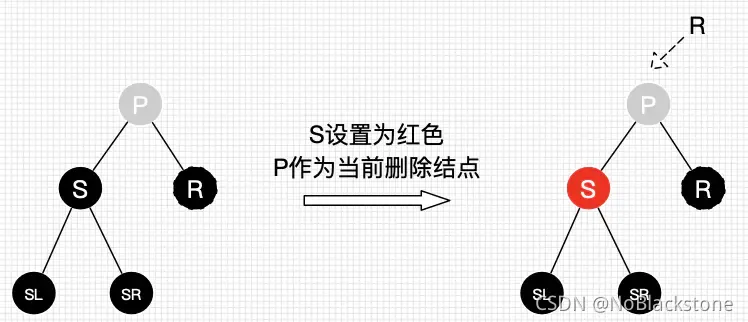
2.2.2.3、替代节点的兄弟节点的子节点都为黑色节点

• 处理：
  • 将 兄弟节点设为红色节点；
  • 将 父节点作为新的替代节点；
  • 根据新的替代节点使用对应删除情景的处理；

2.3、删除情景：总结

• ①、自己能搞定（1、删除情景）；
• ②、自己不能搞定就让兄弟帮忙（除了1、删除情景，2.1.2.3、删除情景，2.2.2.3、删除情景）；
• ③、兄弟都不行，通过父辈，找远房帮忙（2.1.2.3、删除情景，2.2.2.3、删除情景）；