开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【剑指Offer】分治算法 -> 正文阅读

[数据结构与算法]【剑指Offer】分治算法

励志

Love isn’t about ridiculous little words. Love is about grand gestures.
爱不是简单的几个字，爱要付诸行动。

一、剑指 Offer 07. 重建二叉树

题：

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

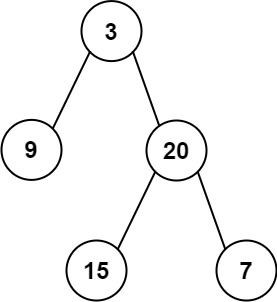
在这里插入图片描述

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

解：

解题思路：前序找根+中序找左右+map定位
AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int[] preorder; // 我们前序找根，中序找左右，主遍历前序数组
    HashMap<Integer, Integer> map = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for(int i = 0; i < inorder.length; i ++) { // 储存中序索引
            map.put(inorder[i], i);
        }
        return recur(0, 0, inorder.length - 1); 
    }
    TreeNode recur(int root, int left, int right) { // root前序坐标，left、right中序坐标
        if(left > right) return null;
        // 建树
        TreeNode tree = new TreeNode(preorder[root]);
        int i = map.get(preorder[root]); // 拿到中序_根节点的坐标
        tree.left = recur(root + 1, left, i - 1);
        tree.right = recur(root + (i - left) + 1, i + 1, right); // 前序：下一右子树root坐标=root+左长度
        return tree;
    }
}

时间复杂度 O(N)：其中 N 为树的节点数量。初始化 HashMap 需遍历 inorder ，占用 O(N) 。递归共建立 N个节点，每层递归中的节点建立、搜索操作占用 O(1)，因此使用 O(N)时间。
空间复杂度 O(N) ： HashMap 使用 O(N) 额外空间；最差情况下（输入二叉树为链表时），递归深度达到 N ，占用 O(N)的栈帧空间；因此总共使用 O(N) 空间。

二、剑指 Offer 16. 数值的整数次方

题：

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

解：

解题思路：快速幂(分治)

快速幂（二进制解析）：

对于一个任何十进制正整数 n ，设其二进制为：“bm…b2b1”

二进制转十进制：
$n=2^0*b_1+2^1*b_2+\cdot \cdot \cdot +2^{m-1}*b_m$ 幂的二进制展开：
$x^n=x^{2^0*b_1+2^1*b_2+\cdot \cdot \cdot +2^{m-1}*b_m}=x^{2^0*b_1}x^{2^1*b_2}\cdot \cdot \cdot x^{2^{m-1}}$

快速幂(二分推导)：
$x^n=\left\{ \begin{array}{l} \left( x^2 \right) ^{n/2},\ n\text{为偶数}\\ x\left( x^2 \right) ^{n/2},\ n\text{为奇数}\\ \end{array} \right.$

AC代码：

class Solution {
    public double myPow(double x, int n) {
        if(x == 0.0d) return 0.0d;
        long pow = n; // 防止-n越界
        if(pow < 0){
            pow = -pow;
            x = 1 / x;
        }
        double res = 1.0;
        while(pow > 0){
            if((pow & 1) == 1) res *= x; // 奇数会损失x
            x *= x;
            pow >>= 1; 
        }
        return res;
    }
}

时间复杂度 O(logn) ：二分的时间复杂度为对数级别。
空间复杂度 O(1) ： res, pow 等变量占用常数大小额外空间。

三、剑指 Offer 17. 打印从 1 到最大的 n 位数

题：

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

说明：

用返回一个整数列表来代替打印
n 为正整数

解：

解题思路：
AC代码：

class Solution {
    public int[] printNumbers(int n) {
        int end = (int)Math.pow(10, n) - 1;
        int[] res = new int[end];
        for(int i = 0; i < end; i ++) {
            res[i] = i + 1;
        }
        return res;
    }
}

时间复杂度 O(10ⁿ)：生成长度为10ⁿ的列表需使用 O(10ⁿ)时间。
空间复杂度 O(1)：建立列表需使用 O(1)大小的额外空间（列表作为返回结果，不计入额外空间）。

四、剑指 Offer 33. 二叉搜索树的后序遍历序列

题：

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

数组长度 <= 1000

解：

解题思路：递归分治

二叉搜索树：左 < 根 < 右

AC代码：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder, 0, postorder.length - 1);
    }
    boolean recur(int[] postorder, int i, int j) {
        if(i >= j) return true; // 递归出口，注意这里是true
        int parent = i; // parent节点坐标
        while(postorder[parent] < postorder[j]) parent ++; // 找第一个右子树节点
        int right_f = parent;
        while(postorder[parent] > postorder[j]) parent ++; // 保证右子树全部大于根节点
        return parent == j && recur(postorder, i, right_f-1) && recur(postorder, right_f, j-1); 
    }
}

时间复杂度 O(N) ：每次调用 recur(i,j)recur(i,j) 减去一个根节点，因此递归占用 O(N)；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用 O(N)。
空间复杂度 O(N)：最差情况下（即当树退化为链表），递归深度将达到 N。

另解：辅助单调栈
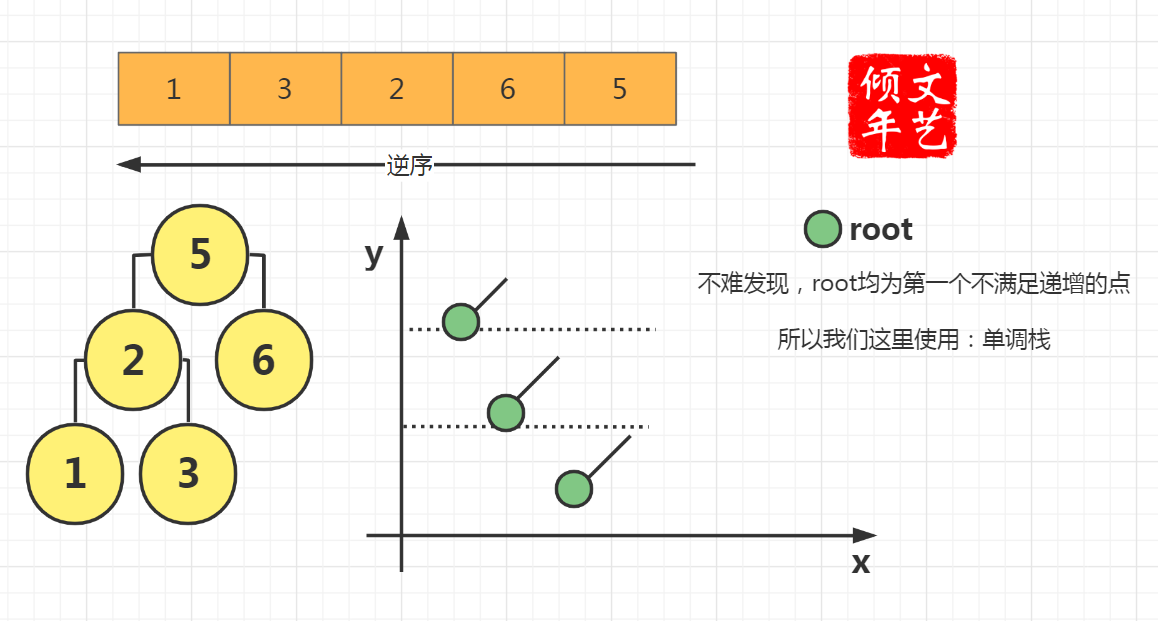
在这里插入图片描述
AC代码：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        Stack<Integer> stack = new Stack<>(); // 单增栈（根->右）
        int root = Integer.MAX_VALUE;
        for(int i = postorder.length - 1; i >= 0; i --){ // 逆序遍历
            if(postorder[i] > root) return false; 
            while(!stack.isEmpty() && stack.peek() > postorder[i]) 
                root = stack.pop(); // 栈顶为当前root
            stack.add(postorder[i]);
        }
        return true;       
    }
}

时间复杂度 O(N) ：遍历 postorder 所有节点，各节点均入栈 / 出栈一次，使用 O(N)时间。
空间复杂度 O(N)：最差情况下，单调栈 stack 存储所有节点，使用 O(N) 额外空间。

五、剑指 Offer 51. 数组中的逆序对

题：

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

解：

解题思路：
AC代码：

class Solution {
    int[] nums, temp; 
    public int reversePairs(int[] nums) {
        this.nums = nums;
        temp = new int[nums.length];
        return merge_sort(0, nums.length - 1);
    }
    int merge_sort(int l, int r) {
        if(l >= r) return 0;
        // 分
        int m = (l + r) / 2;
        int res = merge_sort(l, m) + merge_sort(m + 1, r);
        // 治
        for(int k = l; k <= r; k ++) {
            temp[k] = nums[k]; // temp暂存待合并元素
        }
        int i = l, j = m + 1; // 指向左右首尾元素,这里需要与temp对应
        for(int k = l; k <= r; k ++) {
            if(i == m + 1){
                nums[k] = temp[j ++];
            }else if(j == r + 1 || temp[i] <= temp[j]){
                nums[k] = temp[i ++]; // 默认前者小于后者
            }else{
                nums[k] = temp[j ++];
                res += m - i + 1; // [i,m][m,x) x->i 需要跨越的区间
            }        
        }
        return res;
    }
}

另解：利用之前的模板

class Solution {
    int[] nums; 
    public int reversePairs(int[] nums) {
        this.nums = nums;
        return merge_sort(0, nums.length - 1);
    }
    int merge_sort(int l, int r) {
        if(l >= r) return 0;
        // 分
        int m = (l + r) / 2;
        int res = merge_sort(l, m) + merge_sort(m + 1, r);
        // 治
        int[] temp = new int[r - l + 1]; // [l,r]
        for(int k = l; k <= r; k ++) {
            temp[k - l] = nums[k]; // temp暂存待合并元素
        }
        int i = l - l, j = m + 1 - l; // 指向左右首尾元素,这里需要与temp对应
        for(int k = l; k <= r; k ++) {
            if(i == m + 1 - l){
                nums[k] = temp[j ++];
            }else if(j == r + 1 - l || temp[i] <= temp[j]){
                nums[k] = temp[i ++]; // 默认前者小于后者
            }else{
                nums[k] = temp[j ++];
                res += m - i + 1 - l; // [i,m][m,x) x->i 需要跨越的区间
            }        
        }
        return res;
    }
}