理论知识

动态规划用于解决多阶段决策问题。
动态规划算法与分治法类似,其基本思想是将待求解的问题分解成若干子问题,先求解子问题,再结合这些子问题的解得到原问题的解。但适用于动态规划法求解的问题经分解得到的子问题往往不是互相独立的。
特点1:重复子问题
因存在大量重复子问题,才需要记录之前计算的结果。
如果能够保存已解决的子问题的答案,在需要时再找出以求得的答案,这样可以避免大量重复计算。可以用一个表来记录所有已解决的子问题的答案。
特点2:最优子结构
不同问题规模之间的关系,问题的最优解包含子问题的最优解。
我们可以通过子问题的最优解,推导出问题的最优解。如果我们把最优子结构,对应到我们前面定义的动态规划问题模型上,那我们也可以理解为,后面阶段的状态可以通过前面状态推导出来。
特点3:无后效性
只记录阶段结果,而不关心这个结果是怎么来的。
无后效性,有两层含义,第一层含义是,在推导后面阶段状态的时候,我们只关心前面阶段的状态值,不关心这个状态是怎么一步步推导出来的。第二层含义是,某阶段状态一旦确定,就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型,其实基本上都会满足无后效性。
思维方向1:自顶向下:递归+记忆化
备忘录方法
用表格保存已解决的子问题的答案,在下次需要解此问题时,只要简单的查看该子问题的解答,而非重新计算。
思维方向2:自底向上:递推求解
状态转移方程
一般来说由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
1.状态
状态表示了求解问题的某个阶段;
先看题目问的能不能作为状态;
什么状态好转移,就用什么状态,状态应该为转移方便而服务。
2.状态转移方程
分类讨论
状态转移很多时候就是在做分类讨论,把当前问题分成几个小问题,这些小问题的最优解构成了当前问题的最优解,尝试思考大问题怎么分类。
掌握经典问题的状态设置以及状态转移方程,有些问题很有技巧,需要多做总结。
经典问题1:矩阵连乘
矩阵链连乘问题:
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序 计算矩阵连乘积需要的数乘次数最少。
输入数据:共m+1行;第一行为测试数据的组数m;以后每行n+1个正 整数,表示n个矩阵的行列值。
。
样例输入:
1
5 10 4 6 10 2
输出:最少次数及连乘的计算次序
样例输出:
248
(A1(A2(A3(A4A5))))
状态转移方程
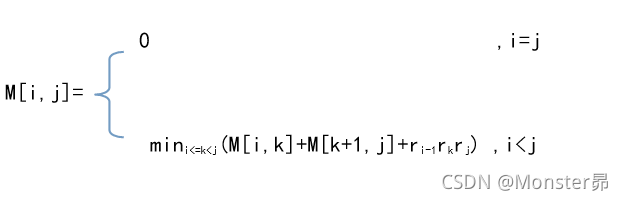
物理意义:
计算Ai*…Aj所需的最小乘法运算次数
#include<stdio.h>
#include<stdlib.h>
int m[50][50],s[50][50];
int p[50];
void MatrixChain(int n);
void Traceback(int i,int j);
int main(void)
{
int count;
scanf("%d",&count);
while(count--)
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&p[i]);
MatrixChain(n);
printf("%d\n",m[1][n-1]);
Traceback(1,n);
printf("\n");
}
return 0;
}
void MatrixChain(int n)
{
for(int i=1;i<=n;i++) //m[i][j]赋值为零 ,作为底
m[i][i]=0;
for(int r=2;r<=n;r++)
{
for(int i=1;i<=n-r+1;i++)
{
int j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i; //记录最优断开位置
for(int k=i+1;k<j;k++)
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
}
void Traceback(int i,int j)
{
if(i==j)
{
printf("A%d",i);
return;
}
printf("(");
Traceback(i,s[i][j]);
Traceback(s[i][j]+1,j);
printf(")");
}
经典问题2:0-1背包
0-1背包问题:
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为c。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
输入:第一行有两个正整数n和W,n是物品种数,W是背包容量,接下来的一行中有n个正整数,表示物品的价值,第三行中有n个正整数,表示物品的重量。
输入样例:
5 10
6 3 5 4 6
2 2 6 5 4
输出:将计算的装入背包物品的最大价值和最优装入方案输出
输出样例:
15
1 1 0 0 1
状态转移方程:

物理意义:
F[i][j]为前i种物品放入容量为j的背包获得的最大价值
#include<iostream>
using namespace std;
void knapSack(int n,int W,int v[],int z[]);
void traceBack(int **F,int v[],int z[],int n,int W);
int main(void)
{
int n,W;
cin>>n>>W;
int *v,*z;
v=new int [n];
z=new int [n];
for(int i=1;i<=n;i++)
cin>>v[i];
for(int i=1;i<=n;i++)
cin>>z[i];
knapSack(n,W,v,z);
return 0;
}
void knapSack(int n,int W,int v[],int z[])
{
int **F;
F=new int*[n+1];
for(int i=0;i<=n;i++)
{
F[i]=new int [W+1];
}
for(int i=0;i<=n;i++)
F[i][0]=0;
for(int j=1;j<=W;j++)
F[0][j]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=W;j++)
{
if(j<z[i])
F[i][j]=F[i-1][j];
else
{
F[i][j]=max(F[i-1][j],F[i-1][j-z[i]]+v[i]);
}
}
}
cout<<F[n][W]<<endl;
traceBack(F,v,z,n,W);
}
void traceBack(int **F,int v[],int z[],int n,int W)
{
int *x;
x=new int [n];
for(int i=n;i>=1;i--)
{
if(F[i][W]==F[i-1][W])
x[i]=0;
else
{
x[i]=1;
W-=z[i];
}
}
for(int i=1;i<=n;i++)
{
cout<<x[i]<<" ";
}
}