二叉搜索树
前言
二分法的数字游戏应该每个人都知道,通过猜测数字与目标数字的大小情况来猜出最终的数字。长度为n的数列,最多需要logn次就能才到真确的数字,即时间复杂度为O(logn)。
二分法的查找过程是,在一个有序的序列中,每次都会选择有效范围中间位置的元素来判断,每次判断后,可以排除一半的元素,直到找到目标元素或者该元素不存在,时间复杂度为O(logn),既然线性结构能够做到查询的时间复杂度为O(logn),然而二叉搜索树查找的时间复杂度为O(logn)-O(n)并不存在查找优势,那为啥还需要二叉搜索树呢?
定义
二叉搜索的定义:
若存在左子树,左子树每个节点的值均小于该节点的值。
若存在右子树,右子树每个节点的值均大于该节点的值。
它的左右子树均是二叉搜索树
图示: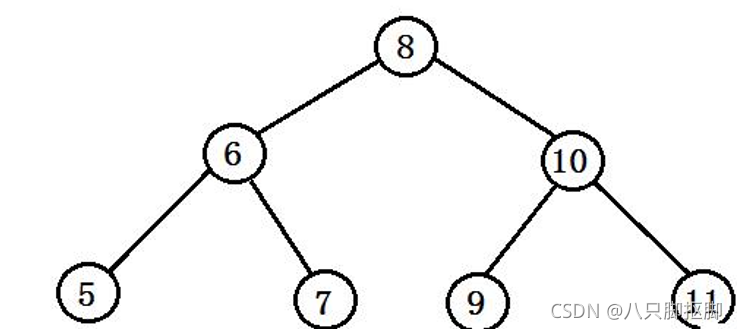
二叉搜索树的基本操作
查找
从根节点开始查找,当当前节点的值小于目标元素的值时,向当前节点的右子树遍历,若当前节点的值大于目标元素的值,就向当前节点的左子树遍历。重复上诉步骤若没找到目标元素,说明树中不存在目标元素,反之就能找到目标元素。
举例:在下图中找到值为9的目标节点,从根节点开始,它小于9因此在他的右子树找,右子树的根节点大于9,因此在它的左子树找,此时当前子树的根节点值等于4,就找了该节点。
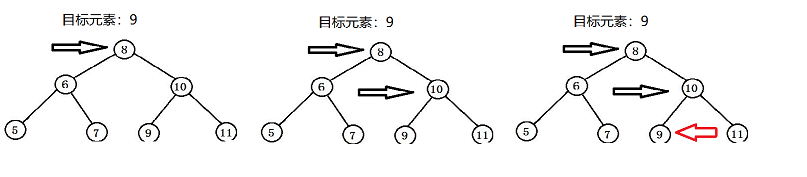
代码实现
//根节点
public Node root;
//创建二叉树节点
class Node{
public int val;
public Node left;
public Node right;
public Node(int val){
this.val = val;
this.left = null;
this.right = null;
}
}
//查找
public Node search(int key){
//从根节点开始遍历
Node cur = root;
while (cur != null){
if (cur.val == key){
return cur;//
}else if (cur.val < key){
cur =cur .right;//小于目标元素就向右子树遍历
}else {
cur = cur.left;//大于目标元素就向左子树遍历
}
}
return null;
}
时间复杂度分析:
时间复杂度:O(logn)级为树的高度。最坏的情况是当树为单支时时间复杂度为:O(n)
插入元素
二叉搜索树的插入操作,就是找到一个适合目标元素的位置,然后将该节点插入二叉搜索树中。插入的元素为叶子节点。
举例:在下面树中插入目标元素9,从根节点开始,9大于8,因此搜索右子树,9小于10,因此搜索10的左子树,但是10没有左子树,因此将9作为10的左子树插入。
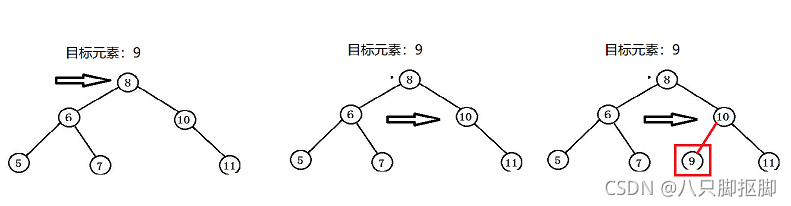
代码实现
//插入
public void insert(int val){
Node newNode = new Node(val);
if (root == null) {
root = newNode;
}else {
Node cur = root;
Node parent = null;
while (cur!=null){
if (cur.val < val){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
if (parent.val > val){
parent.left = newNode;
}else {
parent.right = newNode;
}
}
}
时间复杂度:
与搜索一样,插入的时间复杂度为O(logn)
删除操作
1)找到要删除的目标元素
2)情况1:当目标元素的左子树为null
1.目标元素为根节点 root = root.right;
2.目标元素在父亲节点的右边 parent.right = cur.right;
3.目标元素在父亲节点的左边 parent.left = cur.right;进行上述操作就完成了删除步骤。

情况2:目标元素的右子树为null; 1.目标元素为根节点 root = root.left; 2.目标元素在父亲节点的左边 parent.left = cur.left; 3.目标元素在父亲节点的右边 parent.right = cur.left;进行上述操作就完成了删除步骤。

情况3:左右子树均不为null 通过与右子树的最小值替换或左子树的最大值替换,删除右子树的最小值或右子树的最大值。 1.找到右子树的最小值或者左子树的最大值 2.将找到的值赋值给目标元素节点 3.删除找到右子树的最小值节点或者左子树的最大值节点

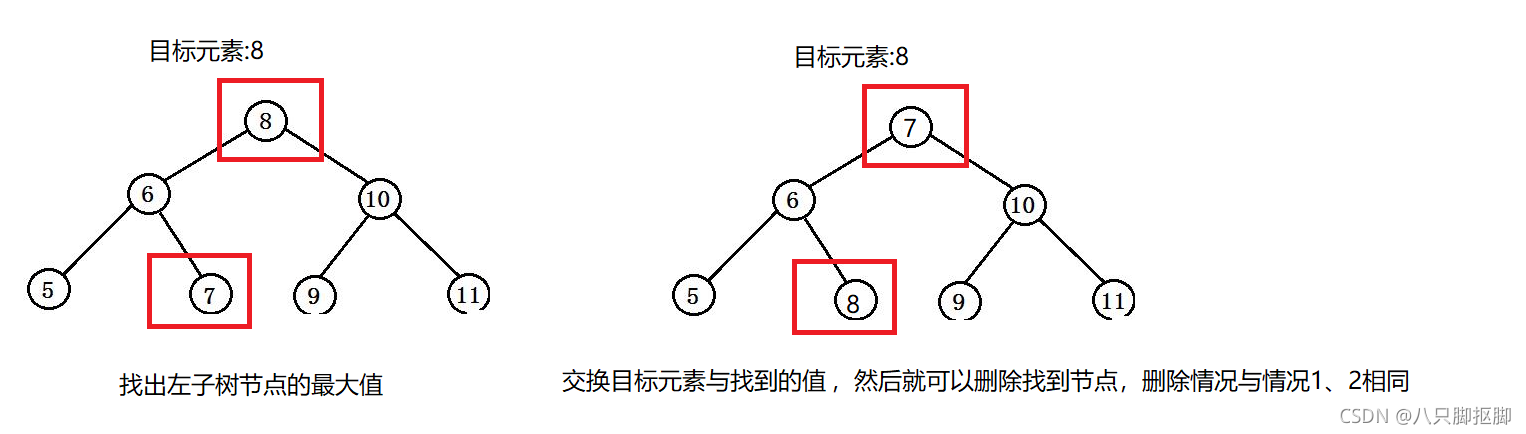
代码实现
//删除
public void remove(int key){
Node cur = root;
Node parent = null;
//先找到该节点
while (cur != null){
if(cur.val == key){
removeKey(cur,parent);
}else if (cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
private void removeKey(Node cur, Node parent) {
//当该节点为左子树为空
if (cur.left == null){
if (cur == root){
root = cur.right;
}else if (parent.left == cur){
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if (cur.right == null){
if (cur == root){
root = cur.left;
}else if (parent.left == cur){
parent.left = cur.left;
}else {
parent.right = cur.right;
}
}else {
//当左右子树都不为null时找到左子树的最大值 或者右子树的最小值(本代码找右子树的最大值)
Node target = cur.right;
Node targetParent = cur;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if (targetParent.left == target){
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
复杂度分析:
时间复杂度:O(logn).
