题目

题目链接：141. 环形链表
在这里插入图片描述

思路–快慢指针

带环问题的链表最大的问题是，遍历链表得不到任何有用的信息，因为代换链表没有NULL，所以不知道到哪里结束！
所以我们有一种思路就是：快慢指针解决！

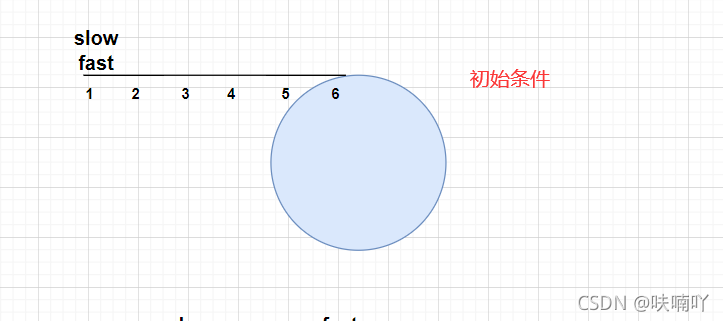
先让slow 走一步，再让 fast 走两步；
同时判断 slow 于 fast 是否相等；
如果相等表示有环，如果没相等那么继续遍历下去；
如果遍历到fast 或者 fast->next 等于NULL，表示没环，否则重复上面的步骤

在这里插入图片描述

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head;
    struct ListNode* fast = head;

    //当链表为偶数时候，判断条件尾fast == NULL就结束：表示没环
    //当链表为奇数时候，判断条件为fast->next == NULL结束表示没没环
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;

       //那么fast开始追击slow,追到表示有环，没追到表示没环！
       //追到的意思是 fast == slow
        if(fast == slow)
        {
            return true;
        }
    }
    return false;
}

证明慢指针走一步，快指针走两步相遇一定有环的问题

假设链表有环，那么快慢指针一定会在环中循环的走，并且快指针先比慢指针进环，当慢指针进环的时候，假设快指针还有N步就追上慢指针，那么当快指针每走两步，慢指针每走一步，导致的结果就是快指针每次都比原来少一步就可以追上慢指针，那么快慢指针一直在环中循环着走，每次快指针每走两步，慢指针每走一步，快指针追到慢指针的距离少一，直到减到0，那么表示快指针和慢指针相遇了，此时就一定存在环！
假如不存在环，那么快指针每走两步，慢指针每走一步时候，它们之间的距离只会越来大，两者不肯相遇！

在这里插入图片描述

带环中，fast走n步（n>2）能否与slow相遇呢？

结论不一定！
假设fast走3步，slow走一步，在slow进环后，假设fast差N步追上slow,此时，slow每次走一步，fast每次走3步，那么fast距离slow就会比原来少2步距离；
当N为偶数时候，fast 就会一直少2步，直到少到0,表示和slow相遇；
当N为奇数时候，fast也会一直少2步，但是少不到0了，只能少到-1，表示fast超过了slow 1步，那么在这一次肯定是不相遇的，这时候，fast和slow的距离又相差 C -1 步（C表示环的步数）；
当 C-1为偶数时候，那么fast 就会和slow 相差两步的减少，直到减到0步，那么就相遇了；
当C-1为奇数时候，那么fast 就永远不会和slow相遇了，以后也没机会了，因为fast 一直会少2步的距离和slow相遇，由于是奇数，只能永远的到最后少到-1；
在这里插入图片描述