堆的基本操作
有很多种数据结构可以实现最小堆,包括:
完全二叉树,左偏树,斜堆,二项堆,斐波那契堆等等,完全二叉树是这里面内存利用效率最高的。
- top:返回当前的最小值
直接返回根节点,时间复杂度为O(1)
int top()
{
return h[1];
}
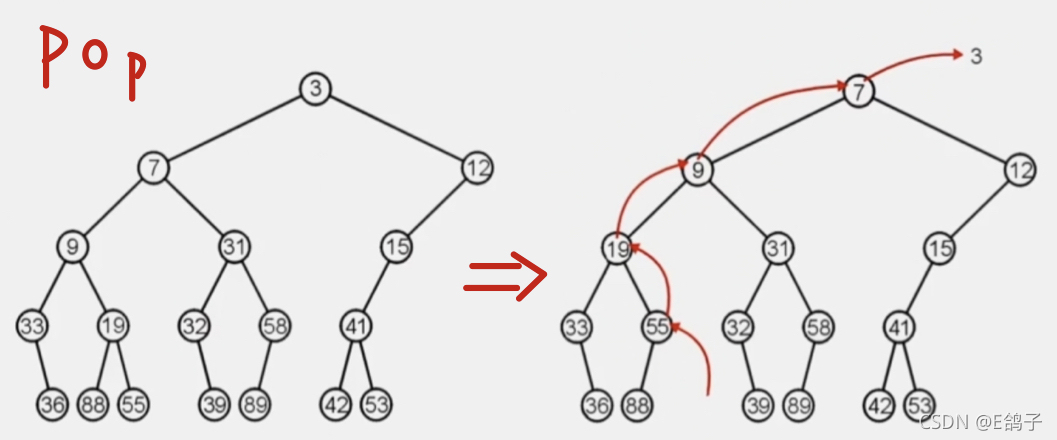
- pop:弹出当前的最小值 (shift_down)
删除根节点,递归把子节点补上来
完全二叉树pop :先把根节点删除,再把最后一个节点移动到根,然后从上往下更新
void pop()
{
h[1] = h[heap_size];
heap_size--;
shift_down(1);
}
- push:插入一个数(shift_up)
插入根,插入一个空节点
第一种情况,可以和当前节点比较,保留较小的,大的递归下去插入子树
第二种情况,如果当前的节点的值小于父节点的值,就和父节点交换,直到大于父节点的值或成为根节点
void push(int v)
{
h[++heap_size] = v;
shift_up(heap_size);
}
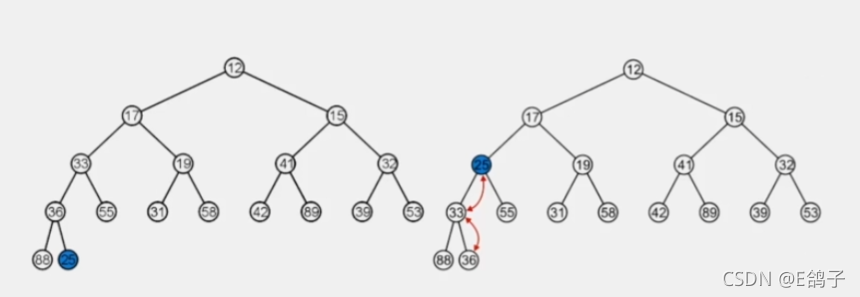
- shift_up
每次将该元素和其父元素比较,若该元素小于其父元素,则将其父元素与其交换位置,直到达到根节点或者该元素大于其父元素
void shift_up(int x)
{
if(x == 1)
return;
if(h[x] < h[x/2])
{
swap(x , x / 2);
shift_up(x / 2);
}
}
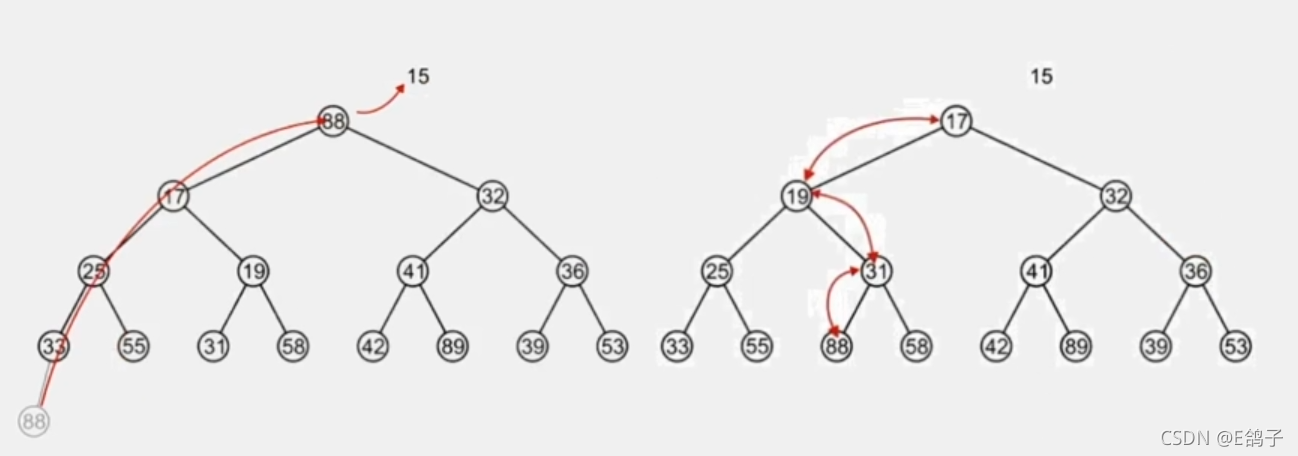
- shift_down
每次将该元素与其左右元素比较,若该元素大于任意一个左右子元素,则将其与左右子元素中的最小的那个交换位置,直到达到叶节点或者该元素小于其两个左右子元素
void shift_down(int x)
{
if(x * 2 > heap_size) //终止条件
return;
int k = x;
if(h[2 * x] < h[k])
k = x * 2;
if(x * 2 + 1 <= heap_size && h[x * 2 + 1] < h[k])
k = k * 2 + 1;
if(k == x)
return;
swap(x , k);
shift_down(k);
}
- 时间复杂度分析:
pop和push的操作都和树的高度正相关
完全二叉树的树高为log n,所以pop和push的时间复杂度均为O(log n)
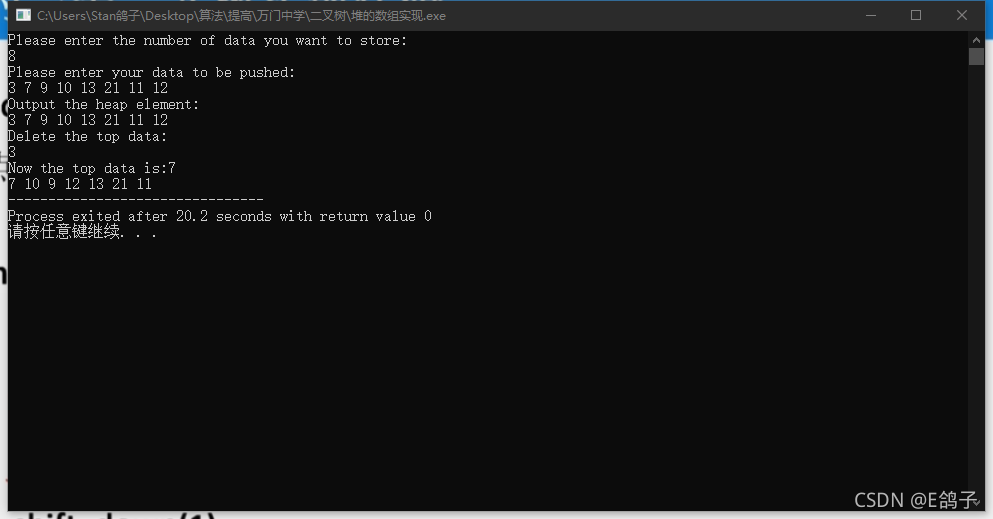
测试代码:
样例pop图:
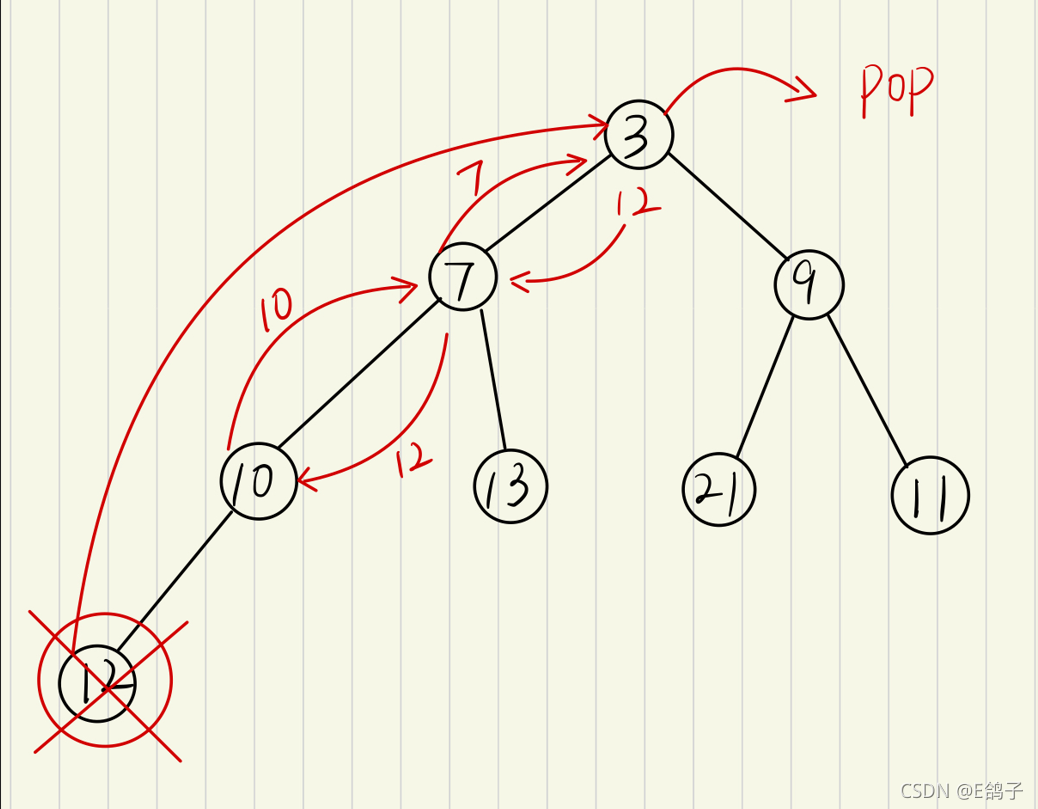
样例:输入3 7 9 10 13 21 11 12 八个数,进行测试
#include <iostream>
#include <cstdlib>
using namespace std;
//首先定义一个数组h[]存储堆元素
//定义一个变量heap_size表示堆的大小
const int N = 1001;
int h[N] , heap_size;
/*
1.top
只需要返回根结点
*/
int top()
{
return h[1];
}
void swap(int x , int y)
{
int temp = h[x];
h[x] = h[y];
h[y] = temp;
}
/*
2.shift_up操作
从节点x开始向根方向依次比较,x的父节点是x/2
*/
void shift_up(int x)
{
if(x == 1)
return;
if(h[x] < h[x/2])
{
swap(x , x / 2);
shift_up(x / 2);
}
}
/*
3.shift_down操作,从节点x开始向子节点方向比较
注意x的左节点是2x,右节点是2x+1
下标不能超过heap_size
*/
void shift_down(int x)
{
if(x * 2 > heap_size) //终止条件
return;
int k = x;
if(h[2 * x] < h[k])
k = x * 2;
if(x * 2 + 1 <= heap_size && h[x * 2 + 1] < h[k])
k = k * 2 + 1;
if(k == x)
return;
swap(x , k);
shift_down(k);
}
/*
4.pop操作
把h[1]和最后一个节点交换,向下比较
*/
void pop()
{
h[1] = h[heap_size];
heap_size--;
shift_down(1);
}
/*
5.push操作
插在最后一个节点,然后向上比较
*/
void push(int v)
{
h[++heap_size] = v;
shift_up(heap_size);
}
int main()
{
int n;
cout << "Please enter the number of data you want to store:" << endl;
cin >> n;
cout << "Please enter your data to be pushed:" << endl;
for(int i = 1 ; i <= n ; i++)
{
int x;
cin >> x;
push(x);
}
cout << "Output the heap element:" << endl;
for(int i = 1 ; i <= heap_size ; i++)
cout << h[i] << " ";
cout << endl << "Delete the top data:" << endl << top() << endl;
pop();
cout << "Now the top data is:" << top() << endl;
for(int i = 1 ; i <= heap_size ; i++)
cout << h[i] << " ";
return 0;
}
运行结果: