最近没有什么事情,打算把之前的作业整理一下发出来,有需要的学弟学妹们可以参考一下。
相关:某电的密码学实验,信安专业必选实验
实验题目:素性检测算法
实验目的
实验环境:
Windows 10
Visual studio 2017
Miracl库
实现目标:
1.通过搭建环境并且实现算法,熟悉运用miracl库的基本函数操作;
2.通过实现fermat素数检测算法,加深对于fermat小定理的理解与运用;
3.体会密码学与数论的紧密联系,将理论化为实践。
方案设计
2.1背景
皮埃尔·德·费马于1636年发现了这个定理。在一封1640年10月18日的信中他第一次使用了上面的书写方式。在他的信中费马还提出a是一个素数的要求,但是这个要求实际上是不必要的。
1736年,欧拉出版了一本名为“一些与素数有关的定理的证明”(拉丁文:Theorematum Quorundam ad Numeros PRIMOS Spectantium Demonstratio)的论文中第一次提出证明,但从莱布尼茨未发表的手稿中发现他在1683年以前已经得到几乎是相同的证明。
有些学家独立制作相关的假说(有时也被错误地称为中国的假说),当成立时,p是素数。这是费马小定理的一个特殊情况。然而,这一假说的前设是错的:例如,341,而341= 11×31是一个伪素数。所有的伪素数都是此假说的反例。如上所述,中国猜测仅有一半是正确的。符合中国猜测但不是素数的数被称为伪素数。
更极端的反例是卡迈克尔数: 假设a与561互质,则 a560被561除都余1。这样的数被称为卡迈克尔数数,561是最小的卡迈克尔数。Korselt在1899年就给出了卡迈克尔数的等价定义,但直到1910年才由卡迈克尔(Robert Daniel Carmichael)发现第一个卡迈克尔数:561。1994年William Alford、Andrew Granville及Carl Pomerance证明了卡迈克尔数有无穷多个。
2.2原理
Fermat小定理:给定素数p,a∈Z,则有a^(P-1)≡1(mod?P )
?奇整数m,若任取一整数2≤a≤m-2,(a,m)=1,使得a^(m-1)≡1(mod?m ),则m至少有1/2的概率为素数
2.3证明过程
证明:├ p┤|a时,a^p (mod?p )≡0,a(mod?p )≡0,即a^p≡a≡0(mod?p )
p?a时,又由于p为素数,故(a,p)=1,由欧拉定理有
a^φ§ ≡1(mod?p )
a^(p-1)≡1(mod?p )
2.4算法步骤
给定奇整数m≥3和安全参数k
随机选取整数α,2≤α≤m-2
计算g=(α,m),如果g=1,转(3);否则,跳出,m为合数
计算r=a^(m-1) (mod?m ),如果r=1,m可能是素数,转(1);否则,跳出,m为合数
重复上述过程k次,如果每次得到m可能为素数,则m为素数的概率为1-1/2^k
方案实现
3.1算法流程图
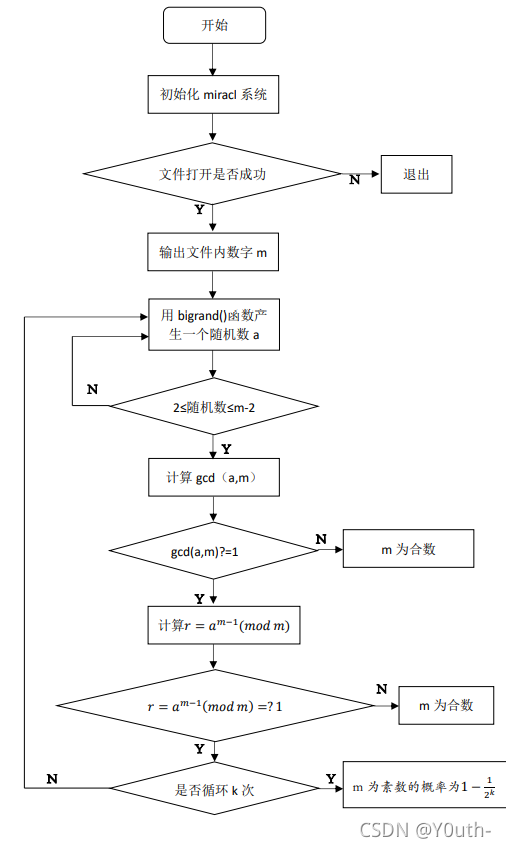
3.2主要函数介绍
(1)mirsys()
函数原型:miracl *mirsys(nd,nb)
参数类型:int nd,nb
功能:初始化MIRACL系统,该函数必须在调用MIRACL库函数之前先执行,函数的返回值是是一个miracl实例指针,通过它可以访问所有实例变量,如果没有足够的内存来创建实例,则为NULL
Eg: miracl *mip=mirsys(500,10);
意思是定义的这些变量最大长度都是500位(这个位是后面进制的位数),输入、输出、运算用的进制都是10进制。
(2)mirvar()
函数原型:flash mirvar(iv)
参数类型:int iv
功能:通过为big/flash变量保留适当数量的内存位置来初始化该变量。这个内存可以通过随后调用mirkill函数来释放, 在程序中,每个big型变量都必须赋初始值,否则会出错。
(3)cinnum()
函数原型:int cinnum(x,f)
参数类型:big x; FILE *f
功能:从键盘或文件中输入一个big类型变量,以实例变量IOBASE的当前值作为数。从键盘输入时,将f指定为stdin,否则指定为其他打开文件的描述符。
(4)cotnum()
函数原型:int cotnum(x,f)
参数类型:big/flash x;FILE *f
功能:将当前分配给实例变量IOBASE的值作为基数,输出一个big/flash的变量到屏幕或文件中参数一个big/flash x和一个文件描述符f。如果f是stdout,则输出到屏幕,否则输出到用描述符f打开的文件。
(5)bigrand()
函数原型:void bigrand(w,x)
参数类型:big w,x;
功能:生成一个大的随机数。使用由irand初始化的内置简单随机数生成器,生成随机数x的范围为0<=x<w
(6)mr_compare()
函数原型:int mr_compare(x,y)
参数类型:big x; big y
函数功能:比较两个大数的大小
返回值:x>y时返回+1, x=y时返回0, x<y时返回-1 在这里需要注意的是,mr_compare()函数比较的是两个big类型的数,此函数的返回值是int型的+1和-1
(7)egcd()
函数原型:int egcd(x,y,z)
参数类型:big x,y,z;
功能:用来计算两个大数的最大公约数, 即z=gcd(x,y)
(8)powmod()
函数原型:void powmod(x,y,z,w)
参数类型:big x,y,z,w;
功能:用来进行模幂运算,用表达式表示为w=x^y mod z
(9)mirexit()
函数原型:void mirkill(x)
参数类型:big x
功能:用来清除MIRACL系统,释放所有内部变量。
3.3算法实现的代码
#include<stdio.h>
#include "miracl.h"
#include<math.h>
#define k 8 //安全参数
int fermat(big m);
int main()
{
big m;
FILE *fp;
//初始化mircal系统
miracl *mip = mirsys(5000, 10);//定义的变量最大长度都是5000位,输入、输出、运算的进制都是10进制
mip->IOBASE = 10; //输入的变量和输出的变量所使用的进制都是10进制
m = mirvar(0);//m为读入的大数
char input[100];//输入文件的文件名
printf("please input your file'name:");
scanf_s("%s", input,100);
fopen_s(&fp, input, "r+");//以可读方式打开 文件必须存在
//文件打开失败
if (fp == NULL) {
printf("File open failed");
return 0;
}
//while (!feof(fp)) {//文件未读取完时,返回值为0
cinnum(m, fp);//将文件中的一个大数赋给m cinnum读取类似于read 有读取指针
printf("The number to be detected is ");
cotnum(m, stdout);
if (fermat(m))
{
printf("This number has a %6.4f%% probability of being a prime number.\n", 100 * (1 - pow(0.5,k)));
}
else
{
printf("This number is a composite number ! \n");
}
//}
return 0;
}
//fermat素性检测算法
int fermat(big m) {
//初始化mircal系统
miracl *mip = mirsys(5000, 10);//定义的变量最大长度都是5000位,输入、输出、运算的进制都是10进制
mip->IOBASE = 10; //输入的变量和输出的变量所使用的进制都是10进制
big a, m1, two, one1;
a = mirvar(0);
m1 = mirvar(0);
copy(m, m1);//m1=m
two = mirvar(2);
one1 = mirvar(1);
int one, i;
one = 1;
decr(m, 1, m1);//m1=m-1
for (i = 0; i < k; i++)
{
//随机选取整数2<=a<=m-2
bigrand(m1, a);//a<m-1 即 a<=m-2
while (mr_compare(two, a)==1)//当2>a时,重新选择 因此2<=a
{
bigrand(m1, a);
}
//计算g(a,m)
big g, r;
g = mirvar(0);
egcd(a, m, g);//g=gcd(m,a)
if (mr_compare(one1, g)==0) {//如果g=1
//计算r=a^m-1(mod m)
r = mirvar(0);
powmod(a, m1, m, r);
if (mr_compare(one1, r)==0)//r=1
{
continue;
}
else
{
return 0;
}
}
else//g!=1
{
return 0;
}
}
mirexit();
return 1;
}
数据分析
通过测试老师验收时所给的大数,来验证编写算法代码的正确性(在代码实现过程中,我所选取的安全参数k为8)
通过多组实验数据验证,运用所编写的算法代码可以将合数检测出来,而所有的素数可以以概率99.6094%确定,因此可以判断所写的fermat素性检测程序没有问题。
总结
在做第一次实验的过程中,首先遇到的困难就是实验环境的搭建,我是采用Windows10+vs2017+miracl库来进行整个实验的,在编译miracl的过程中出现了错误,之后通过不断在网上寻找相应的解决方法和编译miracl库的教程以及询问同学编译miracl的操作,最终成功能够在程序中运用miracl的库函数。
在编程过程中,使用fopen读取文件时报错,This function or variable may be unsafe.
通过网上查询,发现这个问题有很多种解决的办法,我选择了其中的一种,将fopen函数替换为fopen_s()函数,这样做是因为 fopen_s比fopen多了溢出检测,更安全一些。
与我们之前学习c语言的知识相比,在miracl库中,出现了一种新的数据类型,即表示大整数的big数据类型,这种数据类型在使用时不能像使用int数据类型一样进行加、减、乘、除、等于和不等于这样的操作,要使用miracl库中相应的函数,例如:decr()、mr_compare(),以此来实现我们想要的功能。