什么是分治？什么时候用分治？

把大的问题划分为小的问题
设计base case，解决小的问题
可以捕获规模大问题和规模小问题的关系时使用
- 可以用递归
- 可以用动态规划

机器学习中的分治

决策树是一种典型的分治算法；决策树是使用递归实现的。

从数据集中构建决策树的流程如下：

得到原始的数据集，然后基于最好的特征划分数据集，由于特征可能有多个，因此可能存在大于两个分支的数据集划分。
第一次划分之后，数据集将被向下传递到树分支的下一个节点，在这个节点上，可以再次划分数据。所以采用递归的原则处理数据集。

递归结束的条件：

程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。
如果数据集已经处理了所有属性，但是类标签依然不是唯一的，此时我们需要决定如何定义该叶子节点，在这种情况下，我们通常会采用多数表决的方法定义该叶子节点的分类。

参考自： https://blog.csdn.net/beautiful77moon/article/details/98884635

大数据中的分治

分布式计算框架Hadoop通过设计算子，对大问题进行分布式并行处理，最后归并为结果，提高了运算效率。

归并排序

要说 Hadoop MapReduce 就不得不说分治算法，而分治算法其实说白了，就是四个字分而治之。其实就是将一个复杂的问题分解成多组相同或类似的子问题，对这些子问题再分，然后再分。直到最后的子问题可以简单得求解。

要具体介绍分治算法，那就不得不说一个很经典的排序算法 – 归并排序。这里不说它的具体算法代码，只说明它的主要思想。而归并排序的思想正是分治思想。

在这里插入图片描述
二叉树的高 (log2n)，每次用双指针的方式归并，因此扫描数组一遍，复杂度为 $\mathcal{O}(n)$ ；因此归并排序的复杂度是 $\mathcal{O}(nlogn)$ 。

上述的例子这是比较简单的情况，那么我们想想看，当这个数组很大的时候又该怎么办呢？比如这个数组达到 100 GB大小，那么在一台机器上肯定是无法实现或是效率较为低下的。

那一台机器不行，那我们可以拆分到多台机器中去嘛。刚好使用分治算法将一个任务可以拆分成多个小任务，并且这多个小任务间不会相互干扰，可以独立计算。那么我们可以拆分这个数组，将这个数组拆分成 20 个块，每个的大小为 5 GB。然后将这每个 5 GB的块分散到各个不同的机器中去运行，最后再将处理的结果返回，让中央机器再进行一次完整的排序，这样无疑速度上会提升很多。

函数式的 MapReduce

Map 和 Reduce 其实是函数式编程中的两个语义。

Map 和循环 for 类似，只不过它有返回值。比如对一个 List 进行 Map 操作，它就会遍历 List 中的所有元素，然后根据每个元素处理后的结果返回一个新的值。下面这个例子就是利用 map 函数，将 List 中每个元素从 Int 类型转换为 String 类型。

val a:List[Int] = List(1,2,3,4)
val b:List[String] = a.map(num => (num.toString))

而 Reduce 在函数式编程的作用则是进行数据归约。Reduce 方法需要传入两个参数，然后会递归得对每一个参数执行运算。还是用一个例子来说明：

val list:List[Int] = List(1,2,3,4,5)
list.reduce(_ - _)
//运算顺序是：1-2 = -1; -1-3 = -4; -4-4 = -8; -8-5 = -13;
//所以结果等于 -13

参考自：https://www.cnblogs.com/listenfwind/p/9971737.html

分治的度量：Master Therom

主定理，用于计算分治算法的复杂度。
在这里插入图片描述
比较的是 $g=n^{log_{b}{a}}$ 和 $f (n)$ 的阶关系。

如果f大，那么复杂度是 $\mathcal{O}(f(n))$
如果g大，那么复杂度是 $\mathcal{O}(g(n))$
如果f=O(g)，那么复杂度是 $\mathcal{O}(g(n)·log(n))$

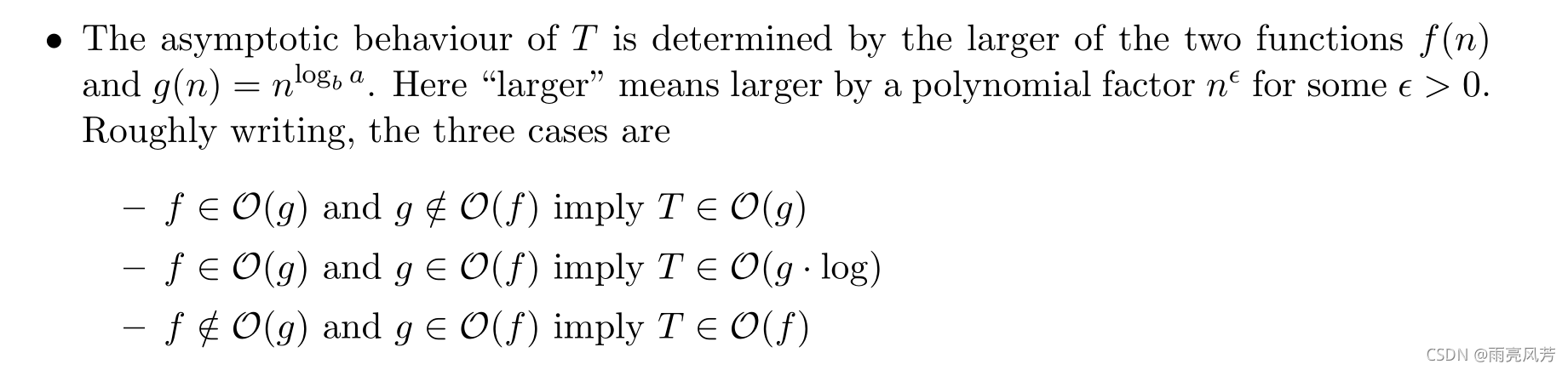
还有一个更加精准的新主定理：

典型例题

集合划分

题目描述
n个元素的集合{1,2,…, n }可以划分为若干个非空子集。
给定正整数n，计算出n 个元素的集合{1,2,…, n }可以划分为多少个不同的非空子集。

输入数据
多组输入(<=10组数据，读入以EOF结尾) 每组一行输入一个数字，n(0<n<=18)

输出数据
每组输出一行结果。

//
// Created by ZixinQin on 2021/9/17.
//
# include <cstdio>
# include <cmath>
# include <iostream>
typedef unsigned long long LL;
using namespace std;

LL reduce(int n, int m){
    if (m == n || m ==1){
        return 1;
    }
    if (m > n || m == 0){
        return 0;
    }
    return m* reduce(n-1,m)+ reduce(n-1,m-1);
}


int main() {
    int n;
    while (cin>>n){
        LL cnt = 0;
        for (int i = 1; i <=n ; ++i) {
            cnt += (LL)reduce(n,i);
        }
        cout<<cnt<<endl;
    }
    return 0;
}

二叉树的后续遍历

题目描述
给你一个二叉树，按照后序遍历的顺序输出这棵树。

输入数据
第一行一个整数 n (1≤n≤1e4) ，表示这棵树的节点数。接下来有 n-1 行，每行有两个整数 u,v ，表示节点 u 到节点 v 有一条边，输入保证树以 1 为根，且 u 为 v 的父节点。对于一个节点的多个子节点，将更早输入的那一个子节点的视为他的左子节点。

输出数据
输出该树的后序遍历，节点编号之间用一个空格分隔。

样例输入
6
1 2
2 3
3 4
1 5
5 6
样例输出
4 3 2 6 5 1
样例说明
后序遍历的定义是：对访问的每个树，先访问他的左子树，然后访问他的右子树，最后访问根节点。

// Created by ZixinQin on 2021/9/17.
# include <cstdio>
# include <cmath>
# include <iostream>
using namespace std;
typedef struct node{
    int data;
    struct node* left;
    struct node* right;
    struct node* parent;
} Node;

typedef struct {
    Node* root;
}Tree;

void postorder(Node* node,char c){
    if (node){
        postorder(node->left,' ');
        postorder(node->right,' ');
        if (c!= NULL)
            printf("%d%c",node->data,c);
        else
            printf("%d",node->data);
    }
}

Node* findroot(Node* node){
    while(node->parent != NULL){
        findroot(node->parent);
    }
    return node;
}

int main() {
    int N;
    scanf("%d",&N);
    Node a[10100];

    for (int i = 1; i <= N; ++i) {
        a[i].parent = NULL;
        a[i].left =NULL;
        a[i].right = NULL;
        a[i].data = i;
    }

    for (int i = 0; i < N-1; ++i) {
        int u,v;
        scanf("%d %d",&u,&v);
        if (a[u].left== NULL){
            a[u].left = &a[v];
            a[v].parent = &a[u];
        } else{
            a[u].right = &a[v];
            a[v].parent = &a[u];
        }
    }
    Node* root = findroot(&a[1]);

    postorder(root,NULL);
}

简单背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8

#include <cstdio>
#include <cmath>
using namespace std;
int dp[1010][1010];
int vol[1010];
int w[1010];
int main(){
    int N,V;
    scanf("%d %d",&N,&V);
    for (int i=1;i<=N;++i){
        scanf("%d %d",&vol[i],&w[i]);
    }
    for (int i=1;i<=N;i++){ // select from top i items
         for (int j=0;j<=V;j++){ // s.t. total volume leq V
            dp[i][j] = dp[i-1][j];
            if (j>= vol[i]){
                dp[i][j] = max(dp[i][j],dp[i-1][j-vol[i]] + w[i]);
            }
         }
    }
    printf("%d",dp[N][V]);
}