?二分搜索的伪码:

?二分搜索的解题思路:
a[1]a[2]a[3]a[4]a[5]a[6]a[7]a[8]
1 2 3 4 5 6 7 8 K=3 //输入8位数的数组
第一次查找: low=1 high=8
mid=(1+8)/2=4 (int整型舍去小数部分)
K=3<a[mid](a[4]=4) 舍去右边大于mid=4的数,这时 high=mid-1=3
↓
a[1]a[2]a[3]
1 2 3 K=3
第二次查找: low=1 high=3
mid=(1+3)/2=2
K=3>a[mid](a[2]=2) 舍去左边小于mid=2的数,这时 low=mid+1=3
↓
a[3]
第三次查找: 3 K=3
? ? ? ? 二分搜索的思路:对比查找元素K,如果刚刚好mid等于K则直接返回mid的位置,如果K大于mid,则把小于mid的数放弃掉,如果K小于mid?,则把大于mid的数放弃掉,相当于直接丢弃一半,一直丢弃,直到找到K等于mid。
?递归代码实现:
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
int Binary_Search(int a[],int k,int low,int high)
{
if(low>high)return 0;
else{
int mid=(low+high)/2;
if(k==a[mid])return mid;
else if(k<a[mid])return Binary_Search(a,k,low,mid-1);
else return Binary_Search(a,k,mid+1,high);
}
}
int main()
{
int k,num;
printf("数组元素个数:");
scanf("%d",&num);
int *a=(int*)malloc(num*sizeof(int));
printf("输入已排序的数组:");
for(int i=1;i<=num;i++) scanf("%d",&a[i]);
while(1){
printf("输入要搜索的值:");
scanf("%d",&k);
int m=Binary_Search(a,k,1,num);
printf("%d的位置在第%d位\n\n",k,m);
}
return 0;
}
结果实现:
线性查找 :
#include <stdio.h>
#include <stdlib.h>
int main()
{
int a[10]={1,2,3,4,5,6,7,8,9,10};
int k;
printf("查找元素:");
scanf("%d",&k);
for(int i=0;i<10;i++){
if(k==a[i]){
printf("%d在第%d位",k,i+1);
}
}
return 0;
}?????????我们可以想,明明可以用几行代码就可以实现一个有序数组的查找,可是为什么偏偏要弄得像二分搜索那样复杂呢??
? ? ? ? 可以直接从“线性查找”的代码看出来,它是一个一个的对比,从0开始到想要搜索的数(即时间复杂度O(n)),这看起来不是比二分搜索更加简洁方便嘛?
? ? ? ?参考一些资料↓


? ? ? ? ?在《算法设计技巧与分析》沙特版中对二分搜索算法的时间复杂度分析为O(log n)
? ? ? ? 通过函数来对比一下y=n与y=log n的差别
? ? ? ? 在0<x<=10之间,两个函数之间的函数值差距开始增大
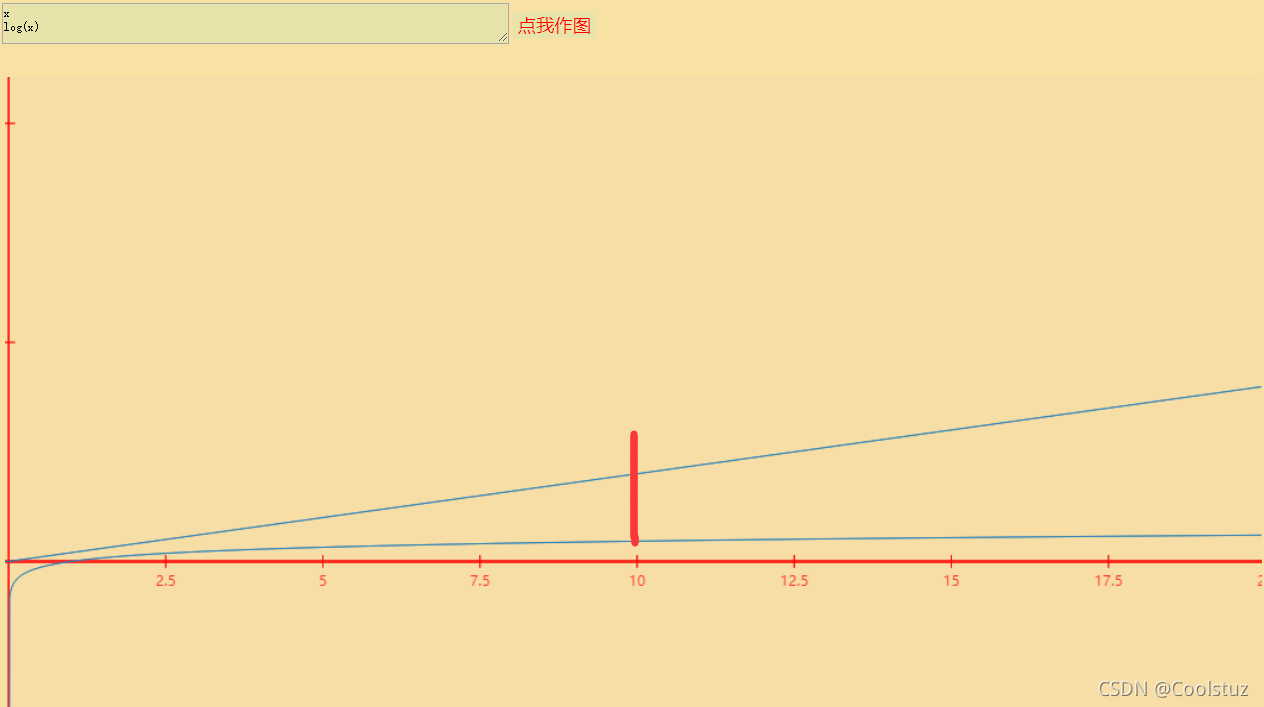
?????????在0<x<=85之间,log n趋于一条直线,而n对应的函数值已经越来越高了
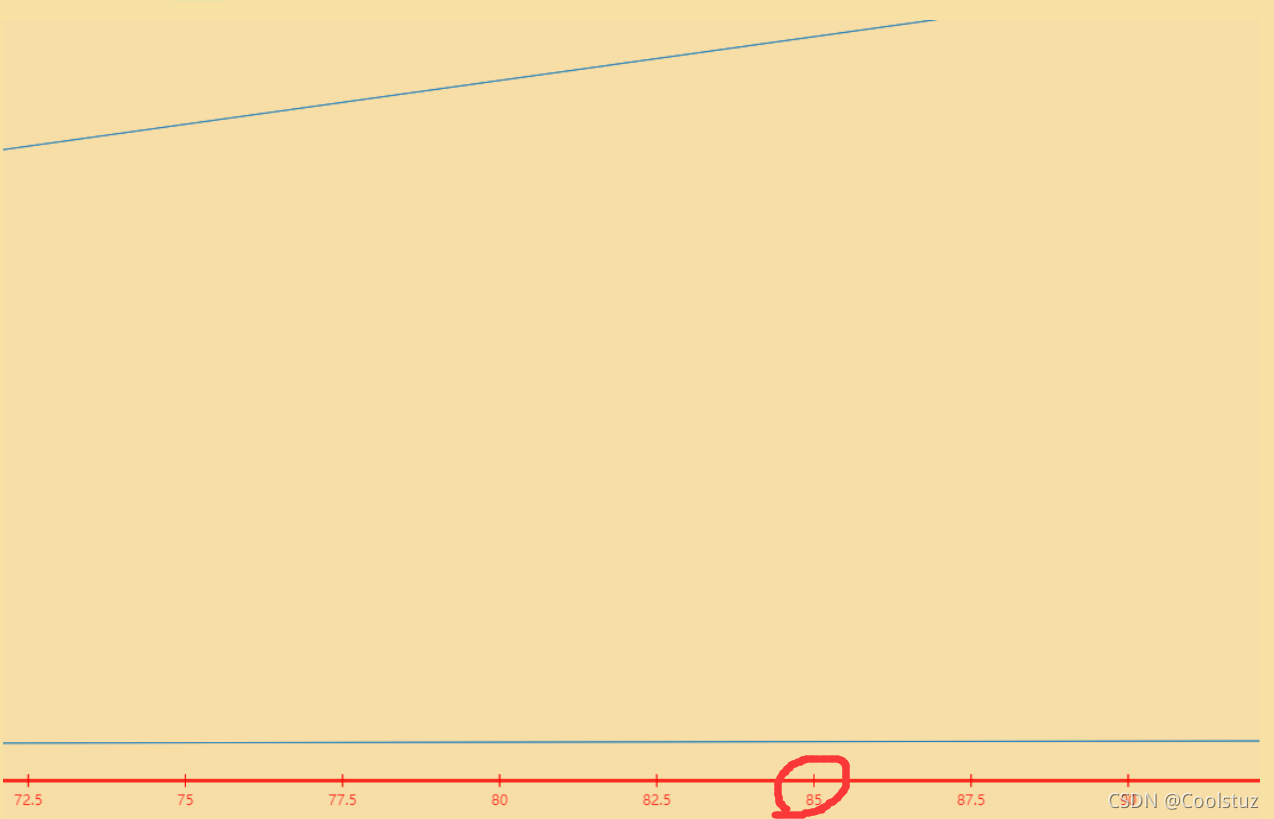
? ? ? ? 由上图可得,当n很大时,线性查找(O(n))所要耗费的时间远远要比二分搜索(O(logn))所耗费的时间要多! 所以二分搜索的重要性是可想而知的,也是必要的!