2021普及组复赛
代码量大点,难度一般。
T1 P7909 [CSP-J 2021] 分糖果
最简单容易想到的思路,应该就是枚举[L,R]范围内的每一个数字 %n 的结果,保留最大结果,如下所示。
//分糖果
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,L,MX=0;
cin>>n>>L>>R;
for(int i=L;i<=R;i++)
{
MX=max(MX,i%n);
}
cout<<MX;
return 0;
}
有的同学可能还会优化一下,因为MX最大为 n-1
//分糖果
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,L,MX=0;
cin>>n>>L>>R;
for(int i=L;i<=R;i++)
{
MX=max(MX,i%n);
if(Mx==n-1)
break;
}
cout<<MX;
return 0;
}
但是这两种方法都不是满分算法,时间复杂度分别为 o(R-L) 和 o(n) ,
结合数据来看的话,都是70分.
继续分析一下
实际问题就是要求 k % n 的最大值, k在 [L,R]范围内.
k % n 的结果,在[0,n-1]范围内。
随着k从L增加R,结果的变化 可以分为两种情况,
达到过 n-1 ,然后到 0 , 然后再继续增加。这种情况答案就是n-1
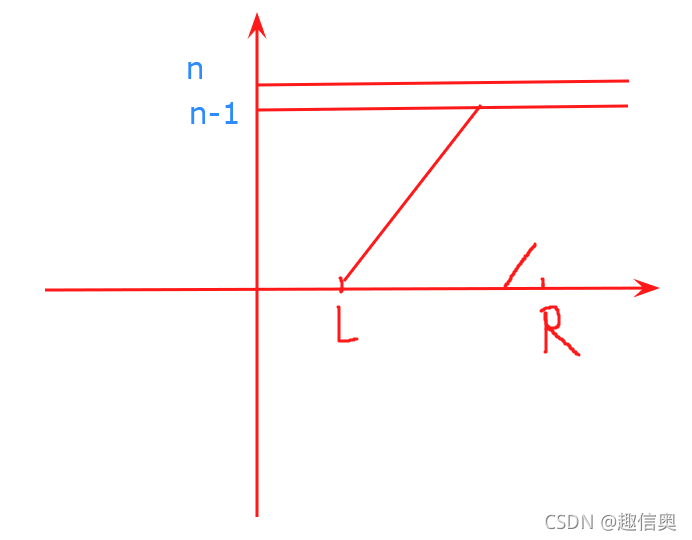
一直增加,这个时候k取R最优
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-94PfyM6e-1635430011173)(NOIP%E7%9C%9F%E9%A2%98.assets/image-20211028211819828.png)]
那么 我们只需要判断 k % n 能不能增加到 n-1。
能的话结果是n-1,不能的话结果是R%n。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,L,R,t,MX=0;
cin>>n>>L>>R;
t=L%n;
if(t+(R-L)>=n-1)
cout<<n-1;
else
cout<<R%n;
return 0;
}
这样o(1)的算法,就可以满分了
T2 P7910 [CSP-J 2021] 插入排序
这个题目可以模拟来做,也可以用树状数组。
考虑到普及组的同学学过树状数组的可能不太多,这里介绍模拟的做法。
这里设计到查询查询元素的原位置,所以用结构体存储值和原来的位置。
题目中有至多5000次的单点修改,每次修改完直接sort()排序时,复杂度为5000 * n * logn,会超时。
熟悉插入排序的话,会发现排序后的元素修改单个元素后的o(n)的时间内就可以完成调整使数组重新有序。单点修改的操作计算量可以优化为 5000 * n.
再结合数据范围来看,查询的次数比较多,而且查询的是原来某个元素排序后的位置,而且这种查询次数在 105 这个级别,所以我们可以把这个数据提前存储下来,从而实现 o(1) 的查询。
这样的话总计算量是 n* logn + 5000 * n + q,结合数据范围看,可以AC。
//插入排序
/*
解题思路:
利用结构体存储每个数字的值和它原来的位置 然后直接进行插入排序
并用 cha数组 记录元素排序后的位置
当需要修改元素时:先找到元素所在位置 修改元素的值 并调整元素的位置 向前或者向后调整 o(n)
查询:直接根据 cha[] 查询 o(1)
*/
#include<bits/stdc++.h>
using namespace std;
struct NUM{
int val,pos;
}num[8010];
int n,cha[8010];//cha 数组方便查询 记录一下原来的第x个元素 现在 在哪个位置
bool cmp(NUM a,NUM b)
{
if(a.val<b.val)
return 1;
else if(a.val==b.val&&a.pos<b.pos)
return 1;
else
return 0;
}
void gai(int x,int v)//把原来的 第x个元素改成v 然后调整数组元素顺序
{
num[cha[x]].val=v;
int i=cha[x];
//接下来可能需要向前调整顺序或者向后调整
while(!cmp(num[i-1],num[i])&&i>1) //向前调整
{
swap(num[i-1],num[i]);
i--;
}
while(!cmp(num[i],num[i+1])&&i<n)//向后调整
{
swap(num[i],num[i+1]);
i++;
}
for(i=1;i<=n;i++)//记录下原来的第x的元素现在到哪了
{
cha[num[i].pos]=i;
}
}
int main(){
int Q;
cin>>n>>Q;
for(int i=1;i<=n;i++)
{
cin>>num[i].val;
num[i].pos=i;
}
sort(num+1,num+1+n,cmp);
for(int i=1;i<=n;i++)//记录下原来的第x的元素现在到哪了
{
cha[num[i].pos]=i;//原来的第pos个元素在下标 i 处
}
while(Q--)
{
int q,x,v;
cin>>q;
if(q==1)
{
cin>>x>>v;
gai(x,v);
}
else
{
cin>>x;
cout<<cha[x]<<endl;
}
}
return 0;
}
T3 P7911 [CSP-J 2021] 网络连接
这也是一道模拟题。
核心在于验证一个IP地址的合法性。
细心验证题目里出现的各个问题即可。
同学们在做的时候除了单独验证某个问题外,还要注意自己的解题方法,会不会因为几个问题叠加在一起,会产生新的问题。
我的代码写法中就有一个 因为两个冒号相连,从而会有一个空数字,调了好久…
//P7911 [CSP-J 2021] 网络连接
/*
解题思路:模拟
check()检查一个ip是否合法
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
map<string,LL>mp;
char s[10],ip[100];
bool check(string a)//检查ip是否合法
{
string op,num;
vector<string>all_num;
for(int i=0;i<a.length();i++)//提取字符和数字
{
if(ip[i]=='.'||ip[i]==':')
{
op.push_back(ip[i]);
all_num.push_back(num);
num.clear();
}
else
{
num.push_back(ip[i]);
}
}
all_num.push_back(num);//最后一个数字 单独存一下
num.clear();
if(op=="...:")//字符顺序对 再检验数字
{
for(int i=0;i<4;i++)
{
if(all_num[i].size()==0)//可能出现两个符号连着 从而出现空数字的情况
return 0;
if(all_num[i].size()>1&&all_num[i][0]=='0')//含前导0 不合法
return 0;
if(all_num[i].length()>3||(all_num[i].length()==3&&all_num[i]>"255"))
return 0;
}
if(all_num[4].length()>5 ||(all_num[4].length()==5&&all_num[4]>"65535"))
return 0;
return 1;
}
else //字符顺序不对 ip不合法
{
return 0;
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%s %s",s,ip);
if(!check(ip))
{
puts("ERR");
continue;
}
if(s[0]=='S')
{
if(!mp[ip])
{
mp[ip]=i;
puts("OK");
}
else
{
puts("FAIL");
}
}
else
{
if(mp[ip]!=0)
printf("%d\n",mp[ip]);
else
puts("FAIL");
}
}
return 0;
}
T4 P7912 [CSP-J 2021] 小熊的果篮
还是模拟…
用双链表数据结构存储所有节点,然后单独存一下每个块的第一个元素编号。
每次输出一个块的头元素并将其删除,同时存储新块的开头的元素,这是一个o(n)的算法,下面直接看代码。
//小熊的果篮
#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int a[N],L[N],R[N];
int main(){
int n;
scanf("%d",&n);
vector<int>b;
for(int i=1;i<=n;i++)//初始化双链表 存储每个块的头元素 位置
{
scanf("%d",&a[i]);
if(i==1||a[i]!=a[i-1])
b.push_back(i);
L[i]=i-1;
R[i]=i+1;
}
R[0]=1,L[n+1]=n;
a[0]=a[n+1]=-1;
while(R[0]!=n+1)//当双链表不空
{
vector<int>c;
for(auto u:b)
{
printf("%d ",u);//输出每个块的头结点
int x=L[u],y=R[u]; //删除已输出的 节点u
R[x]=y,L[y]=x;
if(a[u]==a[y]&&a[u]!=a[x])c.push_back(y);//u和左元素不同且和右元素相同 则是块的起点 就存下来
}
puts("");
swap(b,c);
}
return 0;
}
总体来说难度不高,居然没有dp的题目。