[数据结构与算法] 2021南京大学cs夏令营笔试面试个人总结笔记

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 2021南京大学cs夏令营笔试面试个人总结笔记 -> 正文阅读

[数据结构与算法]2021南京大学cs夏令营笔试面试个人总结笔记

2021南京大学cs夏令营笔试面试个人总结笔记

【非原题】

2021南京大学cs夏令营笔试面试个人总结笔记

0.自我介绍

各位老师好，我是xx软件学院的大三学生。在过去三年的大学学习生活中，我始终严格要求自己，努力学习，积极向上，全面发展自身综合素质。本人的基本情况如下:
我学习认真，专业排名前x%，获得国家奖学金，校级一等奖学金等荣誉，通过四六级考试。
我在大二担任校学生会体育部副部长。同时在班级中担任班长一职。平时生活中，我积极参与志愿服务，在第十届残奥会中担任志愿者；参与“致敬逆行者”公益家教活动。
在大学期间，我参与了一些项目，丰富自己对专业知识的理解和应用。
我参加了“x”的实验室项目，检测x行为。接触了科研的基本流程，增强了调研与阅读英文文献的能力，锻炼了自身创新与科研能力。

我参加了“x”创业项目，项目获得x第四届“筑梦计划”资助名额。

我在去年暑假学校组织的暑期实践中担任队长，实现音乐播放网站的项目。在该项目中，使用vue、Springboot 作为前后端框架、实现了多项功能，通过协同过滤算法实现音乐推荐。提高了我工程开发以及快速学习的能力，增强了团队合作中协作意识。

*我带队参加2021微信小程序开发比赛，*获得全国三等奖，华北赛区一等奖。

在研究生期间，我会积极学习专业知识，协助导师完成各项任务，在研究团队中发挥自己的作用。

1.论文模型选择深度贝叶斯

在深度学习中，和都是一个确定的值，例如。即使我们通过梯度下降（gradient decent）更新，我们仍未改变 “和都是一个确定的值” 这一事实。

那什么是贝叶斯深度学习？将和由确定的值变成分布，这就是贝叶斯深度学习。

贝叶斯深度学习认为每一个权重和偏置都应该是一个分布，而不是一个确定的值。如下图所示，给出一个贝叶斯深度学习示意图：

在这里插入图片描述

2.全局局部变量

作用域：

? 全局变量作用于整个程序；

? 局部变量作用于当前函数。

2.内存分配：

? 全局变量内存分配在自由分配区；

? 局部变量分配在栈区。

3.概率论定理

大数定律说如果统计数据足够大，那么事物出现的频率就能无限接近他的期望值。
（样本足够大）
大数定律说的是随机现象平均结果稳定性。
中心极限定理论证随机变量的和（均值）的极限分布是正态分布。
中心极限定理（CLT）指出，如果样本量足够大，则变量均值的采样分布将近似于正态分布，而与该变量在总体中的分布无关。

4.弗洛伊德（Floyd）算法与迪杰斯特拉（Dijkstra）算法的区别

（1）弗洛伊德（Floyd）算法：图中的每一个顶点都是出发顶点，需要求出每一个被看成为出发顶点的顶点到其他顶点的最短路径
（2）迪杰斯特拉（Dijkstra）算法：选定图中某一个顶点作为出发顶点，求出出发顶点到其他顶点的最短路径

5、解释独立性和相关性；

相关系数为0是两变量独立的必要非充分条件。相关系数反映的是两变量间的线性关系，但是变量间除了线性关系还有其它关系，这时候相关系数就不能作为一种度量了。2、正态分布的性质；
3、正态分布能积分出来么；
4、极限的定义；
5、连续函数的定义；
6、空间闭环曲线怎么求面积或体积；

6、c++面试题

.1.C中static有什么作用

（1）隐藏。当我们同时编译多个文件时，所有未加static前缀的全局变量和函数都具有全局可见性，故使用static在不同的文件中定义同名函数和同名变量，而不必担心命名冲突。

（2）static的第二个作用是保持变量内容的持久。存储在静态数据区的变量会在程序刚开始运行时就完成初始化，也是唯一的一次初始化。共有两种变量存储在静态存储区：全局变量和static变量。

2.多态，虚函数，纯虚函数

多态：是对于不同对象接收相同消息时产生不同的动作。

C++的多态性具体体现在运行和编译两个方面：

*在程序运行时的多态性通过继承和虚函数来体现；*

*在程序编译时多态性体现在函数和运算符的重载上；*

1.C++new和malloc的区别

new操作符从自由存储区(free store)上为对象动态分配内存空间,而malloc函数从堆上动态分配内存。

7、矩阵的特征值怎么求；

Ax=λx (A-λE)x=0

8、C语言的三种分支；

单双多……

10、中断子程序和用户子程序有什么区别；？？
11、损失函数有哪些；？？

激活函数

1.Sigmoid。

特点：
它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.
缺点：
sigmoid函数曾经被使用的很多，不过近年来，用它的人越来越少了。主要是因为它固有的一些缺点。
缺点1：在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

2.tanh（x）

ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。ReLU虽然简单，但却是近几年的重要成果，有以下几大优点：
1）解决了gradient vanishing问题 (在正区间)
2）计算速度非常快，只需要判断输入是否大于0
3）收敛速度远快于sigmoid和tanh

机器学习范式

监督学习

监督学习模型主要可以划分为以下两种：

分类（Classification）：训练的模型主要用于预测类别标签，例如手写数字识别；
回归（Regression）：训练的模型主要用来预测数值，例如房价预测；

无监督学习

聚类（Clustering）：对输入数据进行分组；
密度估计（Density Estimation）：学习输入数据的分布；
可视化（Visualization）：对数据简单进行统计或将高维数据映射到低维向量空间进行可视化；

强化学习

问题：操作系统+计网+机组+数据结构

算法复杂度分析

线性代数

概率论

！！数据结构

操作系统：

内核态用户态

特权指令：只能由操作系统内核部分使用，不允许用户直接使用的指令。

如，进程管理（可软中断）I/O指令、置终端屏蔽jincluding指令、清内存、建存储保护、设置时钟指令（这几种记好，属于内核态）。
非特权指令：

所有程序均可直接使用。

1. 进程progress和线程thread是什么

进程：是进程实体运行的过程，它是系统进行资源分配和调度的一个独立单位。
线程：是操作系统能够进行运算调度的最小单位，是被包含在进程之中的，是进程中的实际运作单位。

（1）根本区别：进程是操作系统资源分配的基本单位，而线程是任务调度和执行的基本单位。

在开销方面：每个进程都有独立的代码和数据空间（程序上下文），程序之间的切换会有较大的开销；线程可以看做轻量级的进程，同一类线程共享代码和数据空间，每个线程都有自己独立的运行栈和程序计数器（PC），线程之间切换的开销小。

所处环境：在操作系统中能同时运行多个进程（程序）；而在同一个进程（程序）中有多个线程同时执行（通过CPU调度，在每个时间片中只有一个线程执行）

进程间通信

每个进程各自有不同的用户地址空间，任何一个进程的全局变量在另一个进程中都看不到，所以进程之间交换数据要靠内核，在内核中开辟一块缓冲区，进程1把数据从用户空间复制到内核缓冲区，进程2再从内核缓冲区把数据读走，内核提供的这种机制称为进程间通信（InterProcess Communication，IPC）。
使用较多的进程间通信的方式主要有以下几种：
①管道（Pipe）及有名管道（Named Pipe）。管道可用于具有亲缘关系进程间的通信，有名管道，除了具有管道所具有的功能外，它还允许无亲缘关系进程间的通信。FIFO
②共享内存（Shared Memory）。可以说这是最有用的进程间通信方式。它使得多个进程可以访问同一块内存空间，不同进程可以及时看到对方进程中对共享内存中数据的更新。这种通信方式需要依靠某种同步机制，如互斥锁和信号量等。
③消息队列（Message Queue）。消息队列是消息的链接表，包括Posix消息队列和SystemV消息队列。它克服了前两种通信方式中信息有限的缺点，具有写权限的进程可以按照一定的规则向消息队列中添加新的信息；对消息队列有读权限的进程可以从中读取消息。FIFO
④信号（Signal）。信号是在权健层次上对中断机制的一种模拟，它是比较复杂的通信方式，用于通知进程有某时间发生，一个进程接收到一个信号与处理器收到一个中断请求效果上可以说是一样的。
⑤信号量（Semaphore）。其主要作为进程之间以及同一进程的不同线程之间的同步和互斥手段。
⑥套接字（Socket）。这是一种更为一般的进程间通信机制，它可用于网络中不同机器之间的进程间通信，应用非常广泛。
线程间通信：

线程间通信常用的方法有如下三种：
①全局变量。由于属于同一个进程的各个线程共享操作系统分配该进程的资源，故解决线程间通信最简单的一种方法是使用全局变量。volatile
②参数传递方式。主线程创建子线程并让其子线程为其完成特定的任务，主线程在创建子线程时，可以通过传给线程函数的参数和其通信。
③Message消息机制。常用的Message通信的接口主要有两个：PostMessage和PostThreadMessage。PostMessage为线程向主窗口发送消息，而PostThreadMessage是任意两个线程之间的通信接口。
④线程同步法。还可以通过线程同步来实现线程间通信。例如有两个线程，线程A写入数据，线程B读出线程A准备好的数据并进行一些操作。这种情况下，只有当线程A写好数据后线程B才能读出，只有线程B读出数据后线程A才能继续写入数据，这两个线程之间需要同步进行通信。
磁盘调度算法
- FCFS先来先服务 First Come First Service
- SSTF最短寻道时间 Shortest Seek Time First选择寻找时间最短的访问者调度
  - 策略：选择使磁头臂从当前位置开始移动距离最短的IO访问者，即最短寻道时间的请求者，
    问题：每次选择距离最短者同时，忽略了可能由于不断的有新的IO请求进程加入队列中，且与当前磁头位置较近，会使得原请求队列中的距离远的访问者总得不到调度，产生"饥饿现象"
- 电梯调度算法（SCAN）
- 磁道编号是从外到里的，即由内到外磁道号越来越小。从当前所在磁道号，从外向里运动，再从里向外运动，或反之。这样就避免了饥饿现象，由于这种移臂调度规律颇似电梯的运动，因而称为电梯算法。
- 循环扫描算法（CSCAN）
  - 为了减少这种延迟，规定磁头单向读/写运动写运动 (如只能由内向外)，完成读写后，立即返到最小/大磁道号的位置 (构成循环 )，再进行扫描。即 CSCAN算法。
分区分配方法
1. 最先匹配法（first-fit）：按分区的先后次序，从头查找，找到符合要求的第一个分区。
  该算法的分配和释放的时间性能较好，较大的空闲分区可以被保留在内存高端。但随着低端分区不断划分而产生较多小分区，每次分配时查找时间开销会增大。
2. 下次匹配法（next-fit）：按分区的先后次序，从上次分配的分区开始查找（到最后分区时再回到开头），找到符合要求的第一个分区。
  该算法的分配和释放的时间性能较好，使空闲分区分布的更均匀，但较大的空闲分区不易保留。
3. 最佳分配法（best-fit）：找打大小与要求相差最小的空闲区。
  从个别来看，外碎片较小，但从整体来看，会形成较多外碎片。较大的空闲分区可以保留。
4. 最坏匹配法（worst-fit）：找到最大的空闲分区。
  基本不留下小空闲分区，但较大的空闲分区不被保留。
分页
页面置换算法
一、最优页面置换算法

最理想的状态下，我们给页面做个标记，挑选一个最远才会被再次用到的页面。当然，这样的算法不可能实现，因为不确定一个页面在何时会被用到。
二、最近未使用页面置换算法（NRU）

系统为每一个页面设置两个标志位：当页面被访问时设置R位，当页面（修改）被写入时设置M位。当发生缺页中断时，OS检查所有的页面，并根据它们当前的R和M位的值，分为四类：

（1）！R&！M（2）！R&M（3）R&！M（4）R&M

编号越小的类，越被优先换出。即在最近的一个时钟滴答内，淘汰一个没有被访问但是已经被修改的页面，比淘汰一个被频繁使用但是“clean”的页面要好。

? 三、先进先出页面置换算法（FIFO）及其改进

这种算法的思想和队列是一样的，OS维护一个当前在内存中的所有页面的链表，最新进入的页面在尾部，最久的在头部，每当发生缺页中断，就替换掉表头的页面并且把新调入的页面加入到链表末尾。

这个算法的问题，显然是太过于“公正了”，没有考虑到实际的页面使用频率。

一种合理的改进，称为第二次机会算法。即给每个页面增加一个R位，每次先从链表头开始查找，如果R置位，清除R位并且把该页面节点放到链表结尾；如果R是0，那么就是又老又没用到，替换掉。

? 五、最近最少使用页面置换算法（LRU）

新数据插入到链表头部；
每当缓存命中（即缓存数据被访问），则将数据移到链表头部；
当链表满的时候，将链表尾部的数据丢弃。

缺页中断发生时，置换未使用时间最长的页面，称为LRU（least recently used）。

LRU是可以实现的，需要维护一个包含所有页面的链表，并且根据实时使用情况更新这个链表，代价是比较大的。

于是，需要对这个算法进行一些改进，也可以说是简化。将每一个页面与一个计数器关联，每次时钟终端，扫描所有页面，将每个页面的R位加到计数器上，这样就大致跟踪了每个页面的使用情况。这种方法称为NFU（not frequently used，最不常用）算法。

这样还是存在一个问题，即很久之前的一次使用，与最近的使用权重相等。

所以，再次改进，将计数器在每次时钟滴答时，右移一位，并把R位加在最高位上。这种算法，称为老化（aging）算法，增加了最近使用的比重。

老化算法只能采用有限的位数，所以可能在一定程度上精度会有所损失。

1. 什么是秩

1. 介绍hashtable

“散列表（Hash table，也叫哈希表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

1. 介绍快排

1. 介绍死锁

1.全概率公式

1. 各种排序算法对比

稳定 ：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
不稳定 ：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
内排序 ：所有排序操作都在内存中完成；
外排序 ：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
时间复杂度 ： 一个算法执行所耗费的时间。
空间复杂度 ：运行完一个程序所需内存的大小。

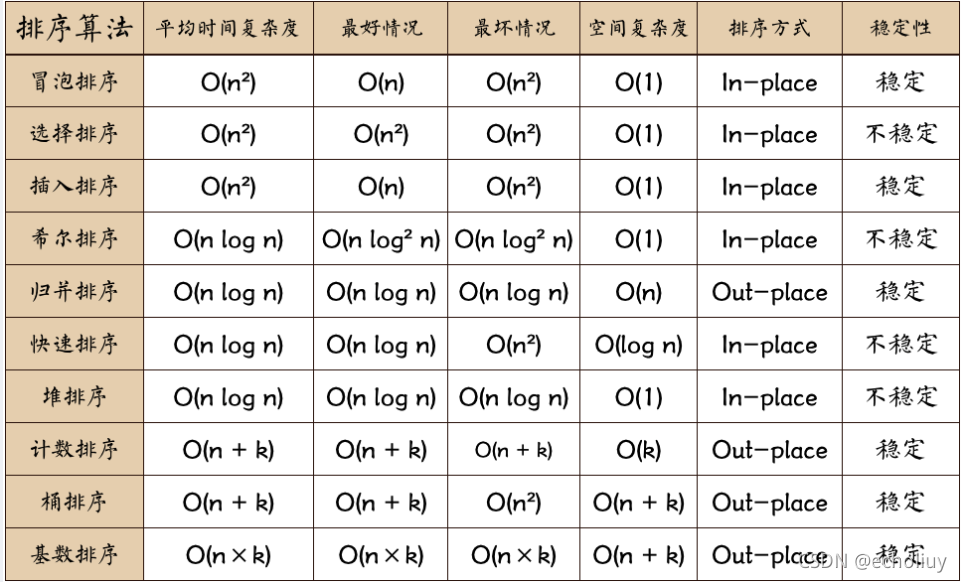
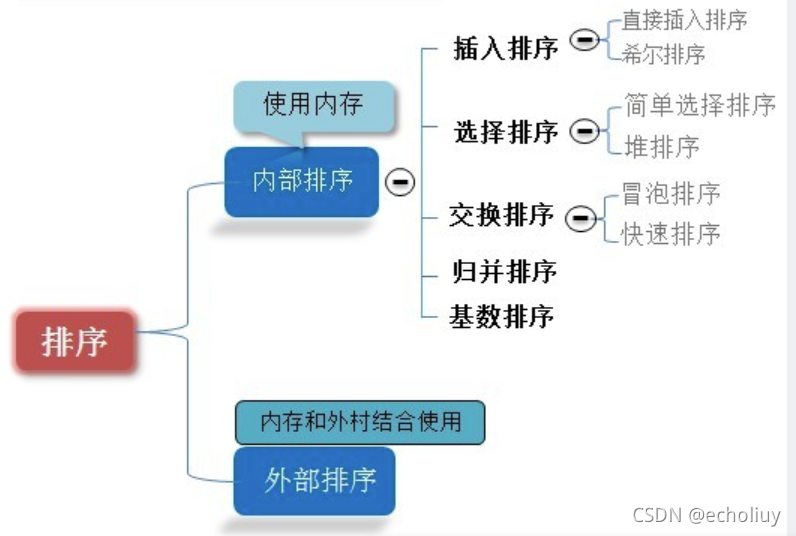
在这里插入图片描述

元素的移动次数与关键字的初始排列次序无关的是：基数排序

元素的比较次数与初始序列无关是：选择排序

算法的时间复杂度与初始序列无关的是：选择排序

1. 冒泡排序（Bubble Sort）稳定

冒泡排序 是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。（把最大的交换到无序区的最后）

步骤1: 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
步骤2: 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

? 稳定排序。

最佳情况：T(n) = O(n)
最差情况：T(n) = O(n2)
平均情况：T(n) = O(n2)

function bubbleSort(arr) {
    varlen = arr.length;
    for(vari = 0; i < len - 1; i++) {
        for(varj = 0; j < len - 1 - i; j++) {
            if(arr[j] > arr[j+1]) {       // 相邻元素两两对比
                vartemp = arr[j+1];       // 元素交换
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    returnarr;
}

2、选择排序（Selection Sort）不稳定

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。（查找最小的放到无序区的最前，保存最小数的索引与第i个交换）

不稳定排序。

最佳情况：T(n) = O(n2)
最差情况：T(n) = O(n2)
平均情况：T(n) = O(n2)

function selectionSort(arr) {
    varlen = arr.length;
    varminIndex, temp;
    for(vari = 0; i < len - 1; i++) {
        minIndex = i;
        for(varj = i + 1; j < len; j++) {
            if(arr[j] < arr[minIndex]) {    // 寻找最小的数
                minIndex = j;                // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    returnarr;
}

3、插入排序（Insertion Sort）稳定

通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

最佳情况：T(n) = O(n)
最坏情况：T(n) = O(n2)
平均情况：T(n) = O(n2)

function insertionSort(arr) {
    varlen = arr.length;
    varpreIndex, current;
    for(vari = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while(preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    returnarr;
}

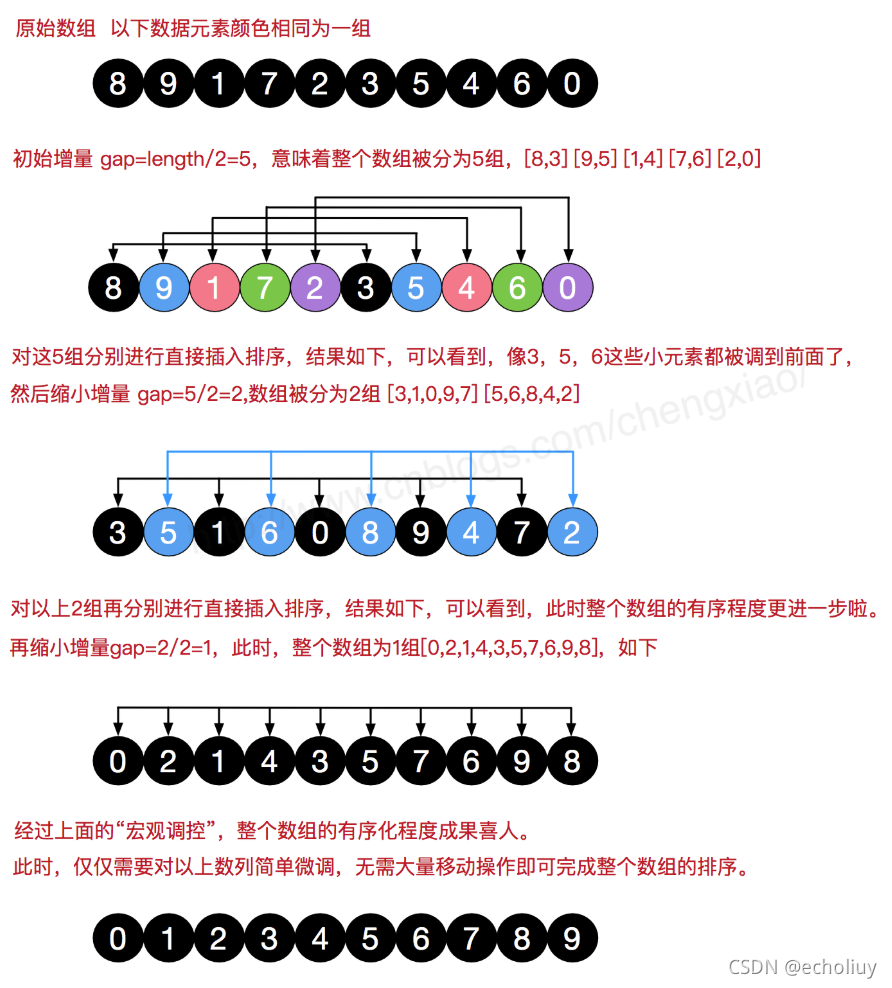
4、希尔排序（Shell Sort）不稳定

希尔排序是把记录按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

? 不稳定排序。

5.归并排序（Merge Sort) 稳定

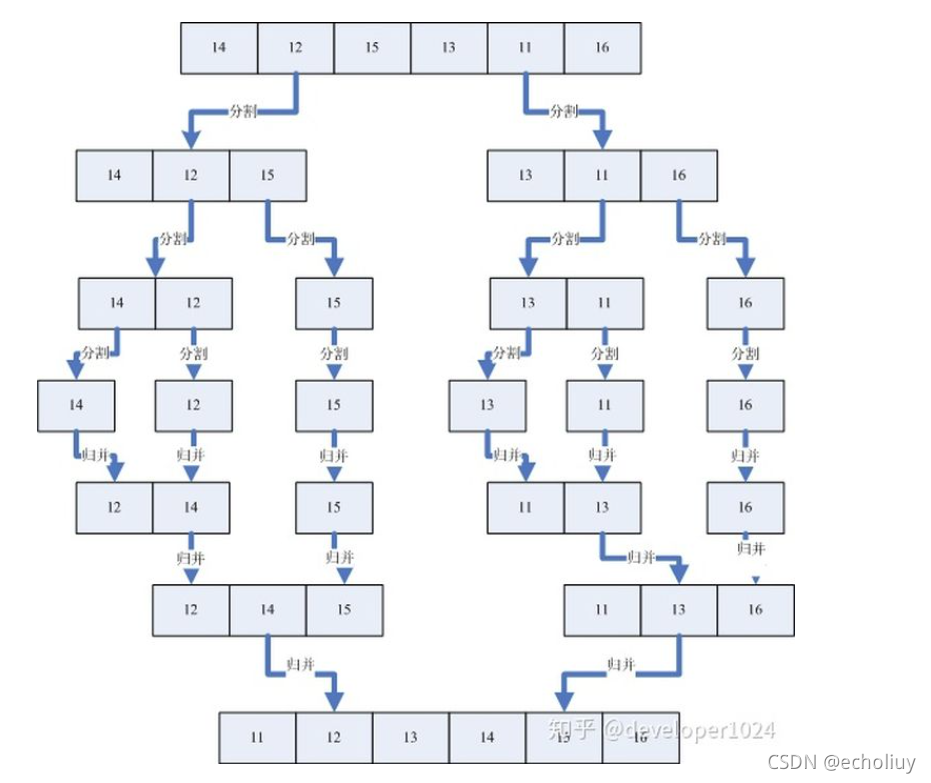
步骤1：把长度为n的输入序列分成两个长度为n/2的子序列；
步骤2：对这两个子序列分别采用归并排序；
步骤3：将两个排序好的子序列合并成一个最终的排序序列。

? 稳定排序。

最佳情况：T(n) = O(n)
最差情况：T(n) = O(nlogn)
平均情况：T(n) = O(nlogn)

6、快速排序 Quick Sort（英语）不稳定

步骤1：从数列中挑出一个元素，称为 “基准”（pivot ）；
步骤2：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
步骤3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

最佳情况：T(n) = O(nlogn)
最差情况：T(n) = O(n2)
平均情况：T(n) = O(nlogn)

优点：缺点：很脆弱，容易平方级
快速排序是原地排序（只需要非常小的一个辅助栈）
快速排序时间消耗，长度为N的数组排序时间与NlgN成正比

public class QuickSort {
	public static void quickSort(int[] arr) {
		// 对函数进行封装
		quickSor(arr, 0, arr.length - 1);
	}
	public static void quickSor(int[] arr, int left, int right) {
		if (left >= right) return;
		int i = left;// 左哨兵
		int j = right;// 右哨兵
		int index = arr[i];// 基准数
		int t = 0;	
		while (i < j) {
			//当右侧数据大于基准数时，右指针向左扫描
			while (arr[j] > index) {
				j--;
			}
			//当左侧数据小于基准数时，左指针右左扫描
			while (arr[i] < index) {
				i++;
			}
			//当二者都停下时，交换数据
			if (i < j) {
				t = arr[i];
				arr[i] = arr[j];
				arr[j] = t;
			}
			//当整个过程完成时，将基准数和分界处的数据互换
			arr[left] = arr[i];
			arr[i] = index;
			//递归处理
			quickSor(arr, left, i - 1);
			quickSor(arr, i + 1, right);
		}
	}
}

快排和归并区别：

归并排序的思路是先递归切割，然后依次向上归并，自下而上完成排序；快速排序则是先划分，再递归切割，然后划分，再切割，切割完成排序完成，自上而下完成排序。

归根到底，归并排序和快速排序在递归和关键操作（归并和划分）执行顺序上的不同，是由归并和划分的本质不同造成的。归并的前提是两个有序数组，所以需要一直递归向下切割直到找到两个只有1个元素的基本数组，然后就可以归并了，所以必须先递归切割再归并；而快速排序的向下递归切割，必须依赖划分的结果（划分完成一次排序，然后返回标杆位置），所以必须先划分再递归切割数组。

7、堆排序 Heap Sort 不稳定

第一个叶子节点，一定是序列长度/2，所以第一个非叶子节点的索引就是arr.length / 2 -1。
// 先根据堆性质，找出它左右节点的索引
int left = 2 * i + 1;
int right = 2 * i + 2;

1、将带排序的序列构造成一个大顶堆，根据大顶堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素；2、将堆顶元素和最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆；3、重复步骤

? 不稳定。

最佳情况：T(n) = O(nlogn)
最差情况：T(n) = O(nlogn)
平均情况：T(n) = O(nlogn)
基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：
- 基数排序： 根据键值的每位数字来分配桶
- 计数排序： 每个桶只存储单一键值
- 桶排序： 每个桶存储一定范围的数值