如何对数据高效排序一直是一个重要的问题,算法中排序分为内部排序和外部排序,而内部排序又分为插入排序、交换排序、选择排序、归并排序等。我们平时常用的冒泡排序和快速排序就属于交换排序。所谓交换就是根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。本篇笔记记录快速排序的思想及实现。
快速排序思想
快速排序是对冒泡排序的一种改进,其基本思想是基于分治法:在待排序表List[1…n]中取任意一个元素p作为基准元素,通过一趟排序将其划分为独立的两个部分List[1…k-1]和List[k+1…n],使List[1…k-1]中的所有元素都小于等于基准元素p,List[k+1…n]中所有元素都大于等于基准元素p,p则最终落在List[k]这个位置,这个过程就是一趟快速排序。然后分别对拆分的两个子表重复上述过程,知道每部分只有一个元素或者空为止,此时所有元素都放在了最终的位置上。
快排算法的关键在于划分操作,同时快排的性能也取决于划分操作的好坏。假设每次总以当前表中第一个元素为基准元素对表划分,那么需要将表中比基准元素大的往右移动,比基准元素小的向左移动。
快速排序图解
我们可以在表的左右两边各设置一个指针,首先从一边开始,假设是右边,那么右指针下的值如果比基准元素大,则指针左移,如果比基准元素小,则将该位置的元素挪到左指针,同时左指针左移,直到移到比基准元素大的位置,将该位置的元素挪到右指针,右指针左移,直到挪到一个比基准元素小的位置…循环往复,知道左右指针碰面,则本趟快排结束。如下图所示。
- 列表的初始状态:

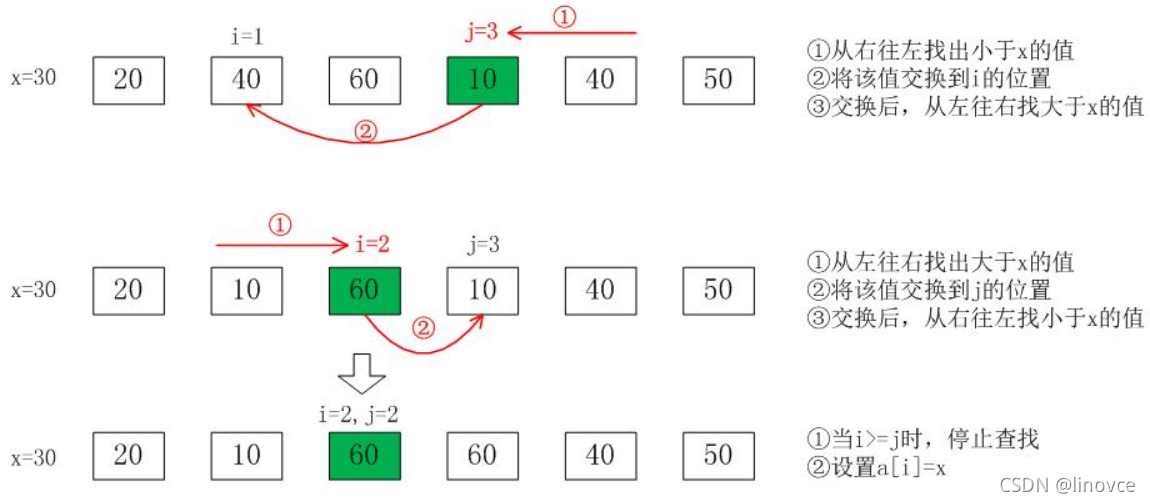
- 从右指针 j 开始找到小于基准元素x的值,把该值交换到左指针 i 的位置:

- 交换后从左指针 i 开始找小于基准元素x的值,将该值换到右指针 j 的位置:

- 循环该过程,直到两指针碰面,停止交换,指针所停位置即为基准元素x=30最终的位置。
- 基准元素将原列表分为左右两个部分,左边元素都小于基准元素,右边部分都大于基准元素。

将两个部分递归执行上述过程,即得到排序后的列表。
代码实现
public static void quickSort(int[] a, int l, int r) {
if (l < r) {
int i = l,j = r,x = a[i];
while (i < j) {
while(i < j && a[j] > x)
j--; // 从右向左找第一个小于x的数
if(i < j)
a[i++] = a[j];
while(i < j && a[i] < x)
i++; // 从左向右找第一个大于x的数
if(i < j)
a[j--] = a[i];
}
a[i] = x;
quickSort(a, l, i-1); // 递归调用划分左边
quickSort(a, i+1, r); // 递归调用划分右边
}
}
参数a为待排序的数组,l和r为此趟快速排序的左右边界,x取左边界的元素作为基准元素。
快速排序算法分析
空间复杂度
因为快速排序时递归的,需要借助一个递归工作栈来保存每层递归调用的必要信息,其容量应与递归调用的最大深度一直,最好情况下为?log(n-1)?;最坏情况下,需要进行n-1次递归调用,展得深度为O(n);平均情况下,栈的深度为O(logn)。因此空间复杂度最坏为O(n);平均情况为O(logn)。
时间复杂度
从上面地流程可以看出,快速排序地运行时间与划分是否对称有关,而后者又与具体使用地划分算法有关,快排有许多划分操作地版本。最坏情况下是划分后两个区域分别包含n-1个元素和0个元素的时候,这种最大程度的不对称如果发生在每层递归上,即初试表基本有序或基本逆序的时候,就得到最坏的时间复杂度O(n2)。
有很多方式可以提高快排的效率:
- 一种方法是当递归过程中划分得到的子序列比较小的时候就不再用递归调用了,二是直接用插入排序算法做后面的排序;
- 二是尽量选取一个可以把数据中分的元素做基准元素。
在最理想的状态下,每次划分都能做到平衡划分,这样时间复杂度为O(nlogn)。
稳定性
在划分时,如果右区间有两个关键字相同,且都小于基准值,那么交换到左区间后,他们的相对位置会发生变化,因此,快排是一种不稳定的排序方式。
例如:List={3,2,2*},结果一次排序后List={3,2*,2},也是最终的排序序列,此时2和2*的相对次序发生了变化。
总结
选取排序方法的时候通常要考虑待排序的元素数目、稳定性要求、存储结构和辅助空间大小等。快速排序被认为是目前内部排序法中最好的方法,当待排序的关键字随机分布时,快排的平均时间最短,如果待排序的元素很多,可以考虑快速排序,不过不是唯一,像堆排序和归并排序等都有各自的优点,后面再记录。
关注下方公众号。该公众号将不定期分享一些小demo、小项目以及学习心得。
往期文章:
