[数据结构与算法]剑指offer50：向下的路径节点之和

题目：
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。
例子：
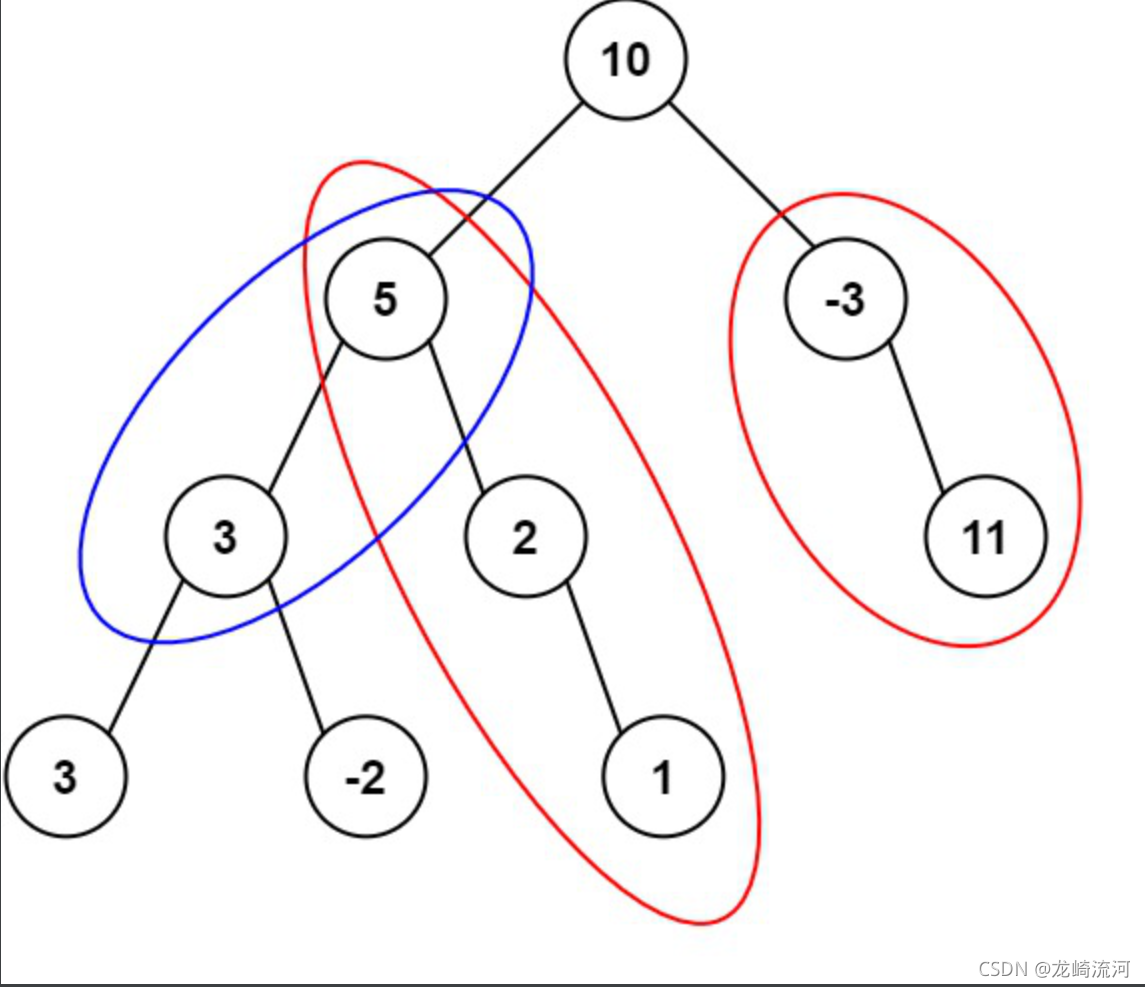
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

分析：

代码以上图例子为例，该题的路径不一定从根节点开始，也不一定到叶子节点结束，路径的起止节点的不确定性给计算路径经过的节点值之和带来了很大难度，如果在路径上移动时把所有累加的节点值之和都保存下来，就容易知道是否存在从任意节点出发的值为给定sum的路径，例如，从二叉树根节点5开始，从根节点开始的路径节点值之和是5，当到达节点2时，从根节点开始的路径节点值之和为7，同理到6时，路径节点值为13，由于要找出节点值之和为8的路径，而13与5的差值为8，这就说明了从节点5的下一个节点也就是节点2开始到节点6结束的路径经过的节点值之和为8，所以这个路径需要保存节点5的值，如果统计的路径sum减去要找到的路径的节点值之和8等于5并且节点5存在，就统计增加一条要求的路径。
因此数据结构可以采用哈希表，哈希表的键就是累加的节点值之和，哈希表的值时每个节点值之和出现的次数，当遍历到一个节点时，就把当前节点的值累加到参数path，如果这个值出现过则将出现的次数加1，如果这个和之前没有出现过，那么就是它第一次出现，然后更新哈希表map保存累加节点值之和path以及出现的次数。该题还是采用递归前序遍历，遍历一个节点后将递归遍历它的子节点，因此，在该函数结束时，程序将回到节点的父节点，因此在函数结束之前，需要将当前节点从路径中删除，从根节点到当前节点累加的节点值之和也要从哈希表map中删除，这是在函数返回之前更新哈希表map把参数path出现的次数减1的原因。
该题详细也可以自己在程序中debug一下，看下这个递归的过程。
代码：

import java.util.HashMap;
import java.util.Map;

public class PathSum {
    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(5);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(4);
        TreeNode node4 = new TreeNode(1);
        TreeNode node5 = new TreeNode(6);
        TreeNode node6 = new TreeNode(3);
        TreeNode node7 = new TreeNode(7);
        node1.left = node2;
        node1.right = node3;
        node2.left = node4;
        node2.right = node5;
        node3.left = node6;
        node3.right = node7;
        int i = pathSum(node1, 8);
        System.out.println(i);
    }
    private static int pathSum(TreeNode root,int sum){
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0,1);
        return dfs(root,sum,map,0);
    }

    private static int dfs(TreeNode root, int sum, Map<Integer, Integer> map, int path) {
        if (root == null){
            return 0;
        }
        path += root.val;
        int count = map.getOrDefault(path-sum,0);
        map.put(path,map.getOrDefault(path,0)+1);
        //count记录路径节点值之和为指定值的次数
        count += dfs(root.left,sum,map,path);
        count += dfs(root.right,sum,map,path);
        //将哈希表中的path对应的次数减1
        map.put(path,map.get(path)-1);
        return count;
    }
}