[数据结构与算法]LeetCode每日一题10.29-11.9

2021.10.29?335. 路径交叉

题目描述

给你一个整数数组 distance 。

从 X-Y 平面上的点?(0,0)?开始，先向北移动 distance[0] 米，然后向西移动 distance[1] 米，向南移动 distance[2] 米，向东移动 distance[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

判断你所经过的路径是否相交。如果相交，返回 true ；否则，返回 false 。

思路

枚举可能产生相交的几种情况

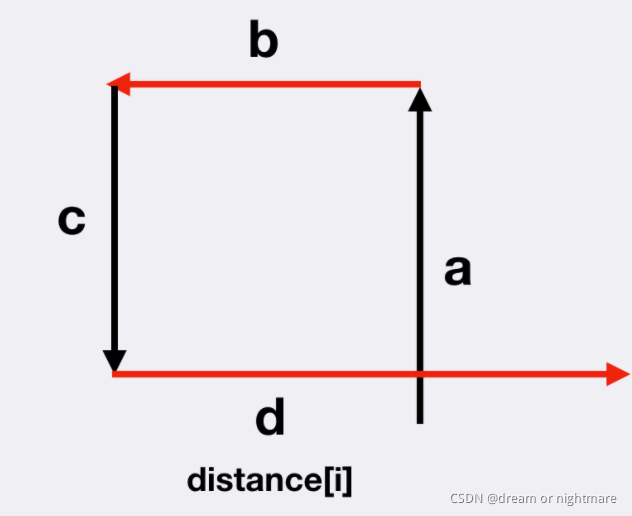
1.d[i] 与 d[i - 3]d[i?3] 发生相交：此时满足 d[i] >= d[i - 2]d[i]>=d[i?2]，同时 d[i - 1] <= d[i - 3]d[i?1]<=d[i?3]；

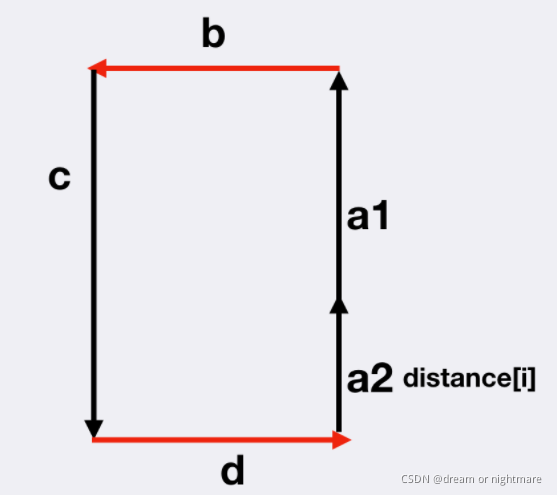
2.d[i] 与 d[i - 4]d[i?4] 发生相交：此时满足 d[i - 1] = d[i - 3]d[i?1]=d[i?3]，同时 d[i] + d[i - 4] >= d[i - 2]d[i]+d[i?4]>=d[i?2]；

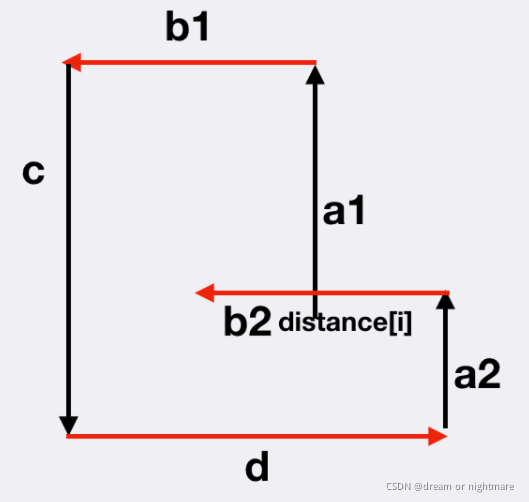
3.d[i]d[i] 与 d[i - 5]d[i?5] 发生相交：此时满足d[i - 1] <= d[i - 3]d[i?1]<=d[i?3]，同时 d[i - 2] > d[i - 4]d[i?2]>d[i?4]，同时 d[i] + d[i - 4] >= d[i - 2]d[i]+d[i?4]>=d[i?2]，同时 d[i - 1] + d[i - 5] >= d[i - 3]d[i?1]+d[i?5]>=d[i?3]。

代码

class Solution {
public:
    bool isSelfCrossing(vector<int>& distance) {
        int n = distance.size();
        if(n <= 3) return false;
        for(int i = 3; i < n; i++) {
            if(distance[i] >= distance[i-2] && distance[i-1] <= distance[i-3]) return true;
            if (i >= 4 && distance[i - 1] == distance[i - 3] && distance[i] + 
distance[i - 4] >= distance[i - 2]) return true;
            if (i >= 5 && distance[i - 1] <= distance[i - 3] && distance[i - 2] >
 distance[i - 4] && distance[i] + distance[i - 4] >= distance[i - 2] && 
distance[i - 1] + distance[i - 5] >= distance[i - 3]) return true;
        }
        return false;
    }
};

2021.10.30?260. 只出现一次的数字 III

题目描述

给定一个整数数组?nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

先看一个简单的题

136.只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？（异或）

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for (auto e: nums) ret ^= e;
        return ret;
    }
};

思路

哈希表、排序等等都不符合线性时间复杂度+空间复杂度O(1)

使用异或

利用除答案以外的元素均出现两次，我们可以先对 numsnums 中的所有元素执行异或操作，得到 sumsum，sumsum 为两答案的异或值（sumsum 必然不为 00）。

然后取 sumsum 二进制表示中为 1 的任意一位 k，sumsum 中的第 k?位为 1?意味着两答案的第 k?位二进制表示不同。

对 numsnums 进行遍历，对第 k 位分别为 0和 1的元素分别求异或和（两答案必然会被分到不同的组），即为答案。

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        int xorsum = 0;
        for (int num: nums) {
            xorsum ^= num;
        }
        // 防止溢出
        int lsb = (xorsum == INT_MIN ? xorsum : xorsum & (-xorsum));
        int type1 = 0, type2 = 0;
        for (int num: nums) {
            if (num & lsb) {
                type1 ^= num;
            }
            else {
                type2 ^= num;
            }
        }
        return {type1, type2};
    }
};

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        int xorsum = 0;
        for(int x:nums){
            xorsum ^= x;
        }
        int k = -1;
        for(int i = 31; i >= 0 && k == -1; i--) {
            if(((xorsum>>i) & 1) == 1) k = i;
        }
        int type1 = 0, type2 = 0;
        for(int x:nums){
            if(((x>>k) & 1) == 1) {
                type1 ^= x;
            }else {
                type2 ^= x;
            }
        }
        return {type1,type2};
    }
};