一、866. 回文素数
1.题目
求出大于或等于 N 的最小回文素数。
回顾一下,如果一个数大于 1,且其因数只有 1 和它自身,那么这个数是素数。
例如,2,3,5,7,11 以及 13 是素数。
回顾一下,如果一个数从左往右读与从右往左读是一样的,那么这个数是回文数。
例如,12321 是回文数。
1 <= N <= 108
答案肯定存在,且小于 2 * 108。
2.分析
这道题一看N的范围,直接跳过暴力枚举求解……QAQ
想了好久怎么入手,是题目的一个示例给了我灵感:

Q:为什么两位数的回文数这么多,居然一个素数都没有?
A:因为两位数的回文数:22、33……88、99全都是11的倍数。
后来用计算器试了一下,果然,偶数位的回文数(除了11)全都不是素数,因为它们都能被11整除。(如:1221、133331、1234554321)
找到了这个切入点,那么思路就有了,这里从总体到细节的逻辑展开:
总体思路:
- 根据n找到最小的回文数,判断该回文数是不是质数,如果不是质数,回文数自增赋值给n,执行下一循环。
细节:
- 确定判断的范围:
正如上文所说,偶数位的回文数(除了11)全都不是素数,因为它们都能被11整除,所以在判断的时候可以以11为分界点,小于等于11和大于11可以分开来判断。
判断小于等于11的代码:
//10之前全都是回文数,直接判断素数
for (int i = n;i <= 11;i++){
if (isPrime(i)){
return i;
}
}
- 缩小回文数的范围:
(1)因为当 n > 11,偶数位数的都没有回文素数,所以判断n为偶数位数时,直接从比当前位数大一位的最小回文数 Math.pow(10, n的位数) + 1e-6 + 1 开始,如:n = 1345,则直接从 10001 开始。
这里返回 当前位数的负数,只要判断得到的回文数是负数,说明n的位数为偶数,直接执行上述公式,从该回文数开始判定。
//偶数位n直接跳过,返回 (- 幂次)
if (s.length % 2 == 0){
return - s.length;
}
(2)除了这个还有吗?当然有!举个例子:213312,这个数很明显不是素数,所以:能被2或5整除的回文数都不是素数(0不用判断,因为回文数如果尾数是0,那么首位也是0了,这是不可能的)
//尾数为偶数和5都不是素数,直接首位自增,其他都改为0,跳到下一循环
if(tmp % 2 == 0 || tmp % 5 == 0){
s[0]++;
for (int i = 1; i <= mid; i++) {
s[i] = '0';
}
continue;
}
- 生成回文数:
(1)回文数是根据n来生成的
(2)回文数是左右对称的
根据以上两个特点,可以从n入手,将 n 通过 String.valueOf(n).toCharArray(); 转换成char类型数组,每位数分存在数组对应下标的位置。这样在生成回文数时,就可以直接操作数组来生成。
// 数组赋值成回文数组
for (int i = 0; i < mid; i++) {
s[s.length -1 - i] = s[i];
}
- 回文数比n小的情况:
(1)这样赋值生成的回文数,有可能会出现比n小的情况:n = 12345,回文数 = 12321
(2)所以需要对生成的回文数进行判断,如果回文数比 n 小,则需要将回文数根加1,再重新生成回文数。
(3)回文数根:回文数 = 12321,该数的回文数根为:123
(4)这里回文数根做加法时,要注意进位(满10进1)
(5)在修改回文数根的时候,不能直接使用前面定义的数组中点下标 int mid = s.length/2; 来作为修改回文数根的指针(我就是踩了这个坑,debug了好几遍才找到……QAQ),否则当 s[mid] = ‘9’ 并修改后,mid会自减,下一次循环就不是 s.length/2了。
//不能直接用mid,否则当s[mid] = '9'并修改后,mid会自减,下一次循环就不是 s.length/2
int index= mid;
while (s[index] == '9'){
s[index--] = '0';
}
s[index]++;
3.代码
public int primePalindrome(int n) {
//10之前全都是回文数,直接判断素数
for (int i = n;i <= 11;i++){
if (isPrime(i)){
return i;
}
}
while (true){
//生成大于n的最小回文数
n = getNextPalindrome(n);
//如果返回负数,说明位数为偶数
if (n < 0){
n = (int) (Math.pow(10, Math.abs(n)) + 1e-6 + 1);
n = getNextPalindrome(n);
}
//判断该回文数是不是素数,是直接返回,不是自增继续下一循环
if (isPrime(n)){
return n;
}
n++;
}
}
// 获取下一个回文数
private int getNextPalindrome(int n) {
char[] s = String.valueOf(n).toCharArray();
//偶数位n直接跳过,返回 (- 幂次)
if (s.length % 2 == 0){
return - s.length;
}
int mid = s.length/2;
while (true) {
// 数组赋值成回文数组
for (int i = 0; i < mid; i++) {
s[s.length -1 - i] = s[i];
}
int tmp = Integer.parseInt(String.valueOf(s));
//尾数为偶数和5都不是素数,直接首位自增,其他都改为0,跳到下一循环
if(tmp % 2 == 0 || tmp % 5 == 0){
s[0]++;
for (int i = 1; i <= mid; i++) {
s[i] = '0';
}
continue;
}
// 如果大于等于n,返回回文数
if (tmp >= n){
return tmp;
}
// 小于n则把回文数根自增,重新生成回文数
else {
//不能直接用mid,否则当mid = 9并修改后,下一次循环就不是 s.length/2
int index= mid;
while (s[index] == '9'){
s[index--] = '0';
}
s[index]++;
}
}
}
//判断是否是素数
private boolean isPrime(int n) {
if (n <= 1){
return false;
}
for (int i = 2;i <= Math.sqrt(n);i++){
if (n % i == 0){
return false;
}
}
return true;
}
二、剑指 Offer 49.丑数
1.题目
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
1 是丑数。
n 不超过1690。
2.分析
- 先列举观察前10个丑数:1, 2, 3, 4, 5, 6, 8, 9, 10, 12
- 因为丑数只包含2、3、5质因子,可以看出:从1以后的任意一个丑数,都可以通过前面的其中一个丑数乘以2 / 3 / 5得到。
方法一、动态规划(数组 + 指针遍历)
- 题目要求第n个丑数,第一时间想到的是用数组来存丑数,最后通过下标n来获取对应的丑数。
- 关于怎么找下一个丑数的问题,先看一张图:
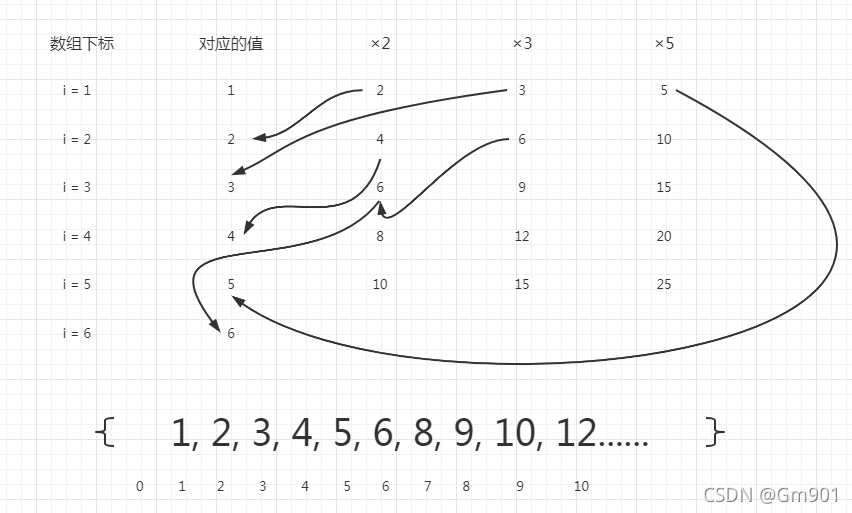
- 通过上图可以看出,每个丑数分别乘以2,3,5,从中取最小丑数存入数组。
- 但是数组的下一个丑数没有明显的规律,所以想了一下,用3个指针来保存乘2,乘3,乘5的丑数的下标。
- 每次都从乘2,乘3,乘5的值中找出乘积最小值的丑数下标,并将乘积存入数组,然后乘该因子的指针右移一位。
- 【注意】这里有可能有一种情况:其中两个乘积相等(如:2 × 3 = 3 × 2 = 6),所以在判断哪个指针应该自增时,不能用 if else,防止一个指针自增完后,跳过了另一个乘积相等的应该自增的指针,导致存入两个相等的丑数。
后来去看了一下官方的题解,发现了另一种方法,效率不算高但是有值得学习的地方,这里也一起展示一下。
方法二、最小堆
这里涉及到的知识点:
- 一种特殊的队列:优先队列(PriorityQueue),属于完全二叉树结构。每次插入或移除元素时,都会对队列进行调整,使得从队列中取出的元素都是队列中最小的。
- 优先队列(PriorityQueue)的一些常用方法:

思路:
- 初始时堆为空。首先将最小的丑数 1 加入堆。
- 每次取出堆顶元素 x,则 x 是堆中最小的丑数,由于2x,3x,5x 也是丑数,因此将2x,3x,5x 加入堆。
上述做法会导致堆中出现重复元素的情况。为了避免重复元素,可以使用哈希集合去重,避免相同元素多次加入堆。 - 在排除重复元素的情况下,第 n 次从最小堆中取出的元素即为第 n 个丑数。
3.代码
方法一、动态规划(数组 + 指针遍历)
public int nthUglyNumber(int n) {
//将丑数存入一个数组中,第n个丑数为 a[n]
int[] result = new int[n + 1];
result[1] = 1;
//需要乘2的下标
int t2 = 1;
//需要乘3的下标
int t3 = 1;
//需要乘5的下标
int t5 = 1;
int i;
for (i = 2;i < result.length;i++){
int a = result[t2] * 2;
int b = result[t3] * 3;
int c = result[t5] * 5;
int min = a < b ? a : b;
min = min < c ? min : c;
if (min == a){
result[i] = min;
t2++;
}
if (min == b){
result[i] = min;
t3++;
}
if (min == c){
result[i] = min;
t5++;
}
}
return result[n];
}
方法二、最小堆
public int nthUglyNumber2(int n) {
int[] factors = {2, 3, 5};
//用于对重复元素去重
Set<Long> seen = new HashSet<>();
PriorityQueue<Long> heap = new PriorityQueue<>();
seen.add(1L);
//将指定的元素插入此优先级队列
heap.offer(1L);
int ugly = 0;
for (int i = 0; i < n; i++) {
//poll() 获取并移除此队列的头
long curr = heap.poll();
ugly = (int) curr;
for (int factor : factors) {
long next = curr * factor;
if (seen.add(next)) {
heap.offer(next);
}
}
}
return ugly;
}