首发公众号
bigsai,首发博客平台csdn,谢绝未联系转载
前言
大家好,我是bigsai,好久不见,甚是想念(天天想念)!
很久前就有小伙伴被动态规划所折磨,确实,很多题动态规划确实太难看出了了,甚至有的题看了题解理解起来都费劲半天。
动态规划的范围虽然确实是很广很难,但是从整个动态规划出现的频率来看,这几种基础的动态规划理解容易,学习起来压力不大,并且出现频率非常高。
这几个常见的动态规划有:连续子数组最大和,子数组的最大乘积,最长递增子序列(LIS),最长公共子序列(LCS),最长公共子串,最长公共子串,不同子序列。
什么是动态规划
首先很多人问,何为动态规划?动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。通俗一点动态规划就是从下往上(从前向后)阶梯型求解数值。
那么动态规划和递归有什么区别和联系?
总的来说动态规划从前向后,递归从后向前,两者策略不同,并且一般动态规划效率高于递归。
不过都要考虑初始状态,上下层数据之间的联系。很多时候用动态规划能解决的问题,用递归也能解决不过很多时候效率不高可能会用到记忆化搜索。
不太明白?
就拿求解斐波那契额数列来说,如果直接用递归不优化,那么复杂度太多会进行很多重复的计算。
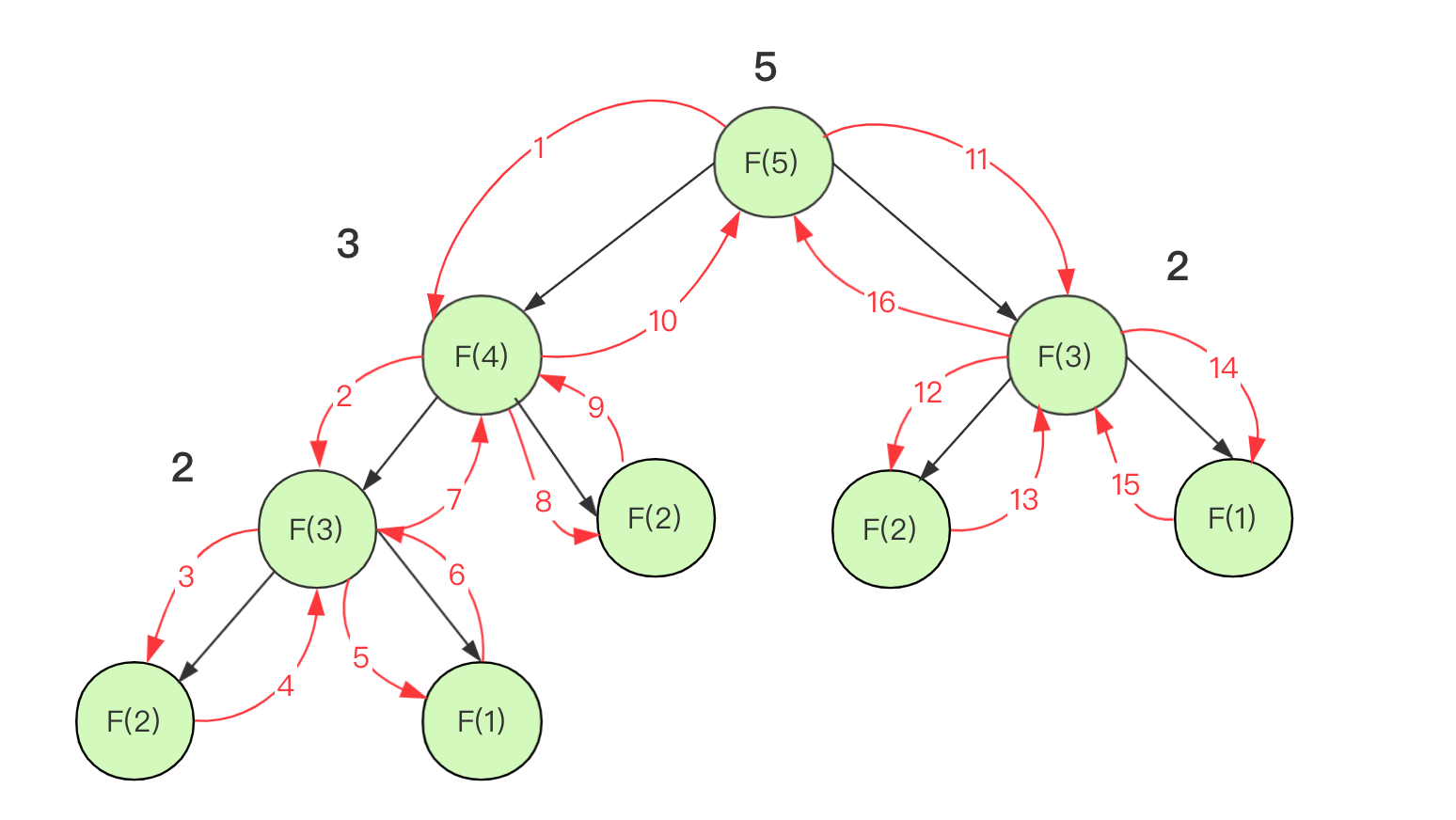
但是利用记忆化你可以理解为一层缓存,将求过的值存下来下次再遇到就直接使用就可以了。
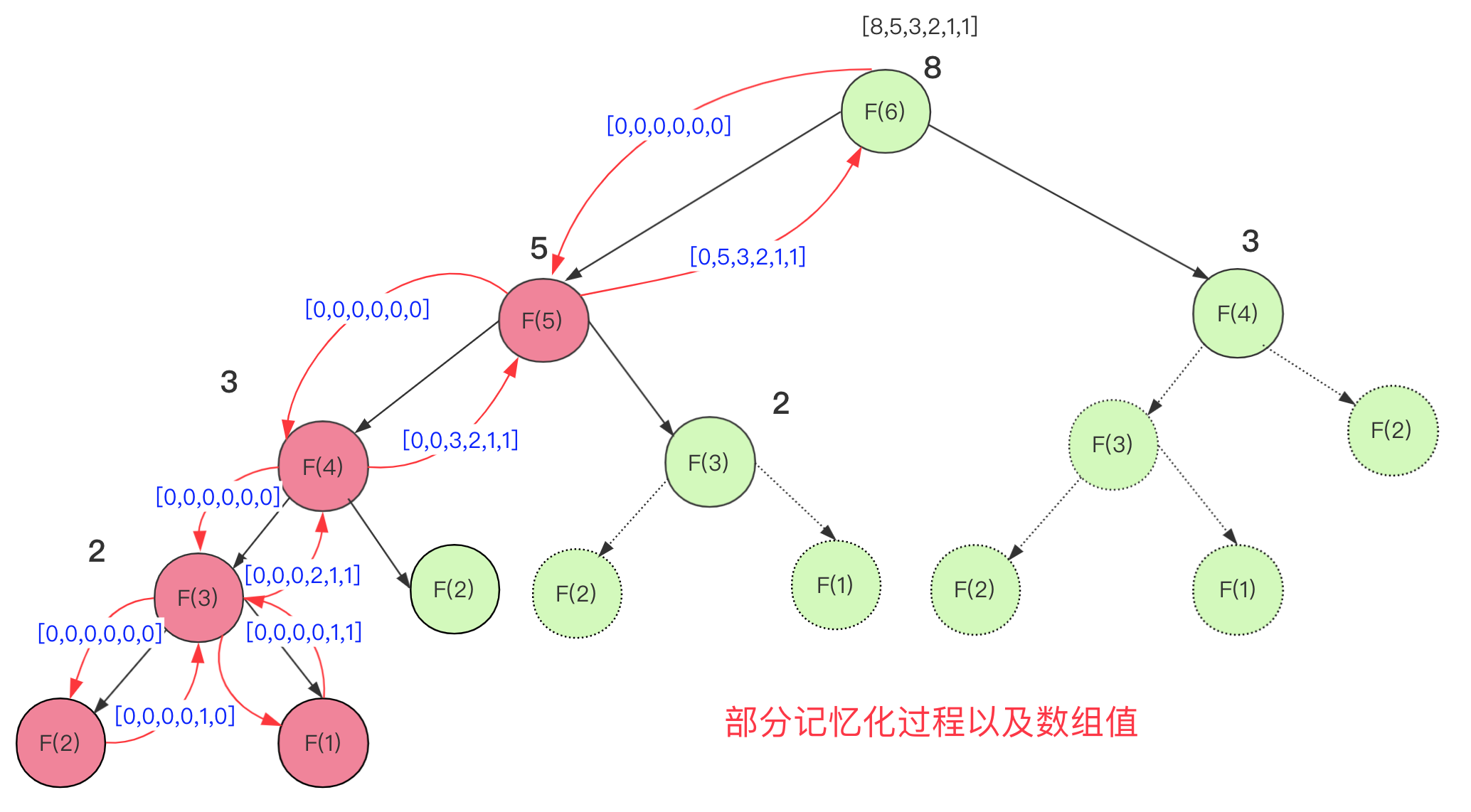
实现记忆化搜索求斐波那契代码为:
static long F(int n,long record[])
{
if(n==1||n==2) {return 1;}
if(record[n]>0)
return record[n];
else
record[n]=F(n-1,record)+F(n-2,record);
return record[n];
}
public static void main(String[] args) {
int n=6;
long[] record = new long[n+1];
System.out.println(F(n,record));
}
而动态规划的方式你可以从前往后逻辑处理,从第三个开始每个dp都是前两个dp之和。
public int fib(int n) {
int dp[]=new int[n+1];
dp[0]=0;
dp[1]=1;
for(int i=2;i<n+1;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
当然动态规划也能有很多空间优化,有些只用一次的值,你可以用一些变量去替代。有些二维数组很大也可以用一维数组交替替代。当然动态规划专题很大,有很多比如树形dp、状压dp、背包问题等等经常出现在竞赛中,能力有限这里就将一些出现笔试高频的动态规划!
连续子数组最大和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
dp的方法就是O(n)的方法。如果dp[i]表示以第i个结尾的最大序列和,而这个dp的状态方程为:
dp[0]=a[0]
dp[i]=max(dp[i-1]+a[i],a[i])
也不难解释,如果以前一个为截至的最大子序列和大于0,那么就连接本个元素,否则本个元素就自立门户。
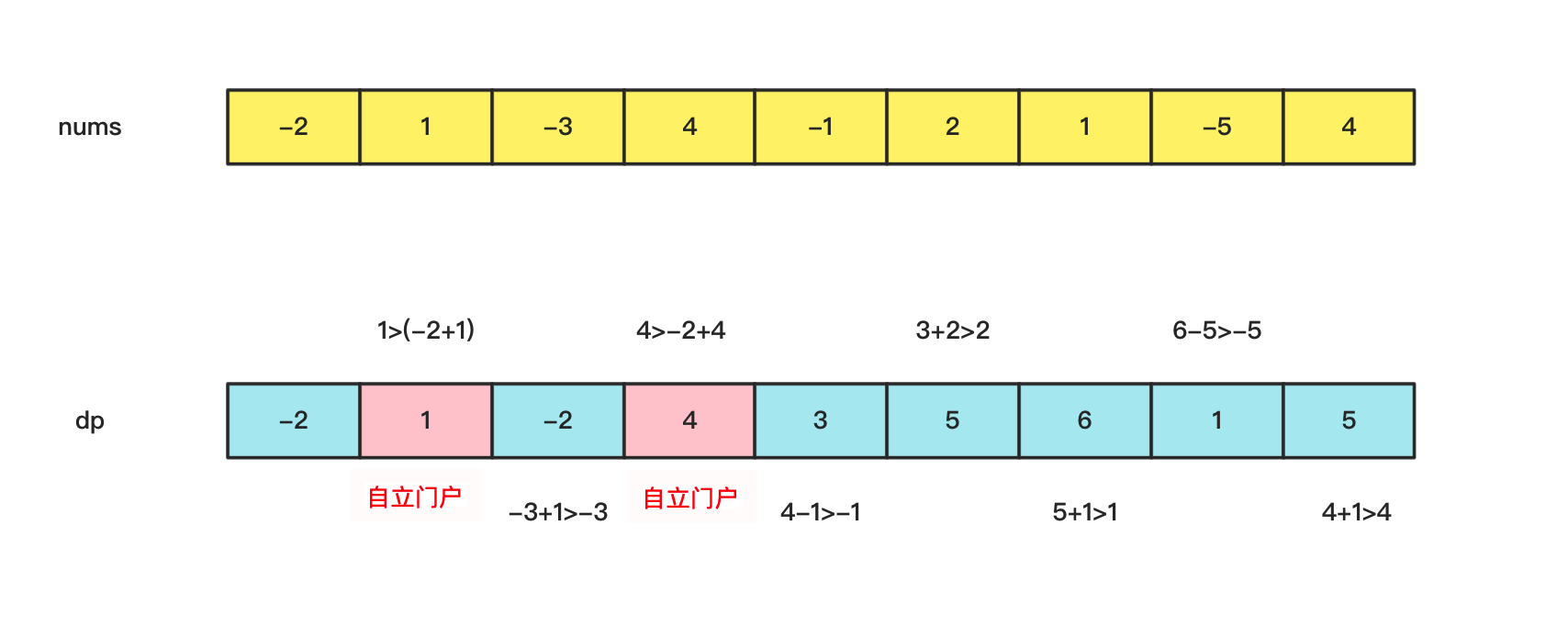
实现代码为:
public int maxSubArray(int[] nums) {
int dp[]=new int[nums.length];
int max=nums[0];
dp[0]=nums[0];
for(int i=1;i<nums.length;i++)
{
dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
if(dp[i]>max)
max=dp[i];
}
return max;
}
ps:有小伙伴问那求可以不连续的数组最大和呢?你好好想想枚举一下正的收入囊中,那个问题没意义的。
连续子数组最大乘积
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
示例 :
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
连续子数组的最大乘积,这也是一道经典的动态规划问题,但是和普通动态规划又有点小不同。
如果数据中都是非负数,对于连续数组的最大乘积,那样处理起来和前面连续子数组最大和处理起来有些相似,要么和前面的叠乘,要么自立门户。
dp[0]=nums[0]
dp[i]=max(dp[i-1]*a[i],a[i])
但是这里面的数据会出现负数,乘以一个负数它可能从最大变成最小,并且还有负负得正就又可能变成最大了。
这时候该怎么考虑呢?
容易,我们开两个dp,一个dpmax[]记录乘积的最大值,一个dpmin[]记录乘积的最小值。然后每次都更新dpmax和dpmin不管当前值是正数还是负数.这样通过这两个数组就可以记录乘积的绝对值最大。
动态方程也很容易
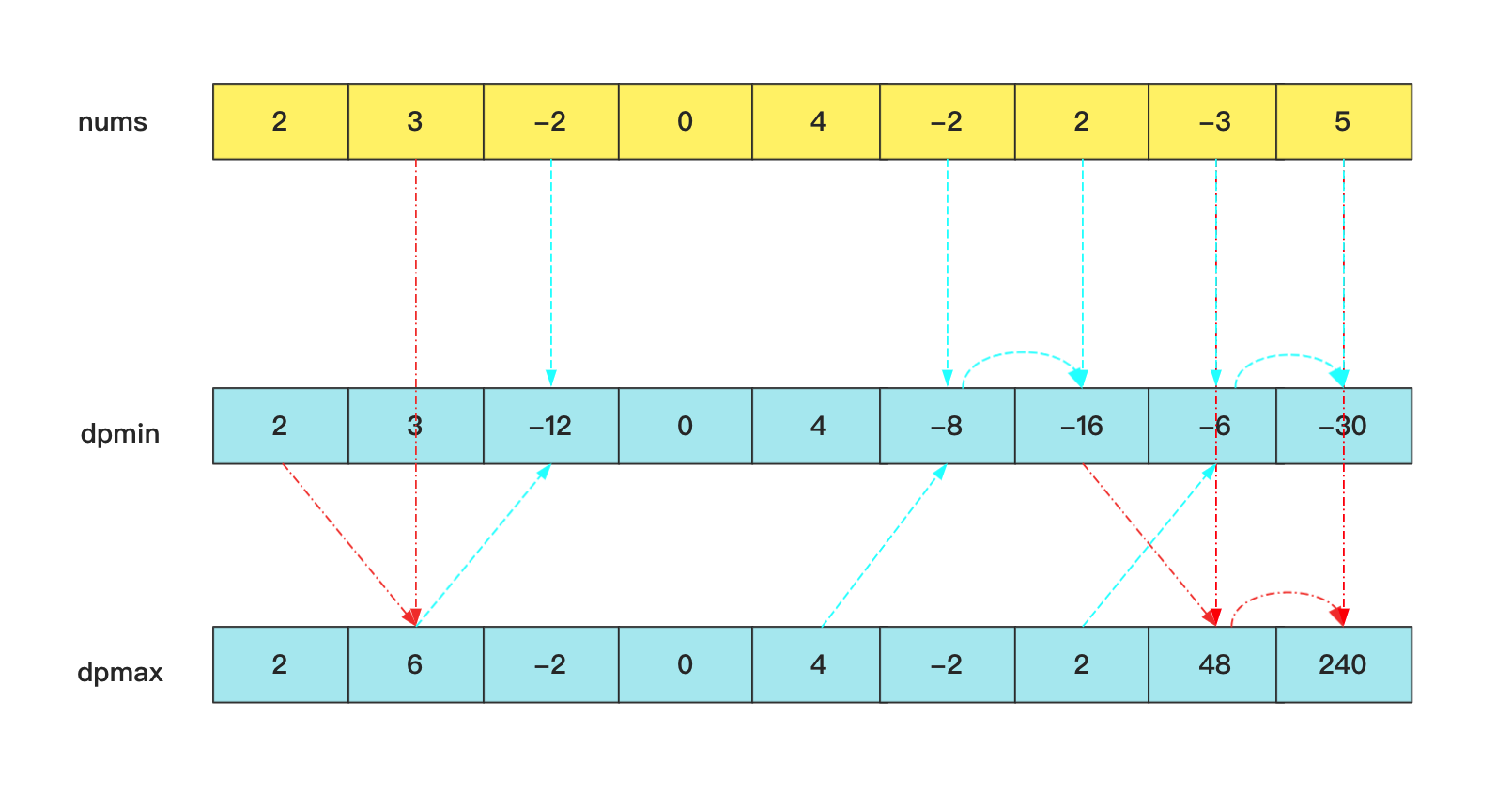
dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
看一个过程就能理解明白,dpmin就是起到中间过度的作用,记录一些可能的负极值以防备用。结果还是dpmax中的值。
最长递增子序列
最长递增子序列,也称为LIS,是出现非常高频的动态规划算法之一。这里对应力扣300
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [0,1,0,3,2,3]
输出:4
解释:最长递增子序列是 [0,1,2,3],因此长度为 4 。
对于最长递增子序列,如果不考虑动态规划的方法,使用暴力枚举其实还是比较麻烦的,因为你不知道遇到比前面元素大的是否要递增。
比如 1 10 3 11 4 5,这个序列不能选取1 10 11而1 3 4 5才是最大的,所以暴力枚举所有情况的时间复杂度还是非常高的。
如果我们采取动态规划的方法,创建的dp[]数组,dp[i]表示以nums[i]结尾的最长递增子序列,而dp[i]的求解方式就是枚举i号前面的元素和对应结尾的最长子序列,找到一个元素值小于nums[i]并且递增序列最长,这样的时间复杂度为O(n2)。
状态转移方程为:
dp[i]=max(dp[j])+1, 其中0≤j<i且num[j]<num[i]
具体流程为:
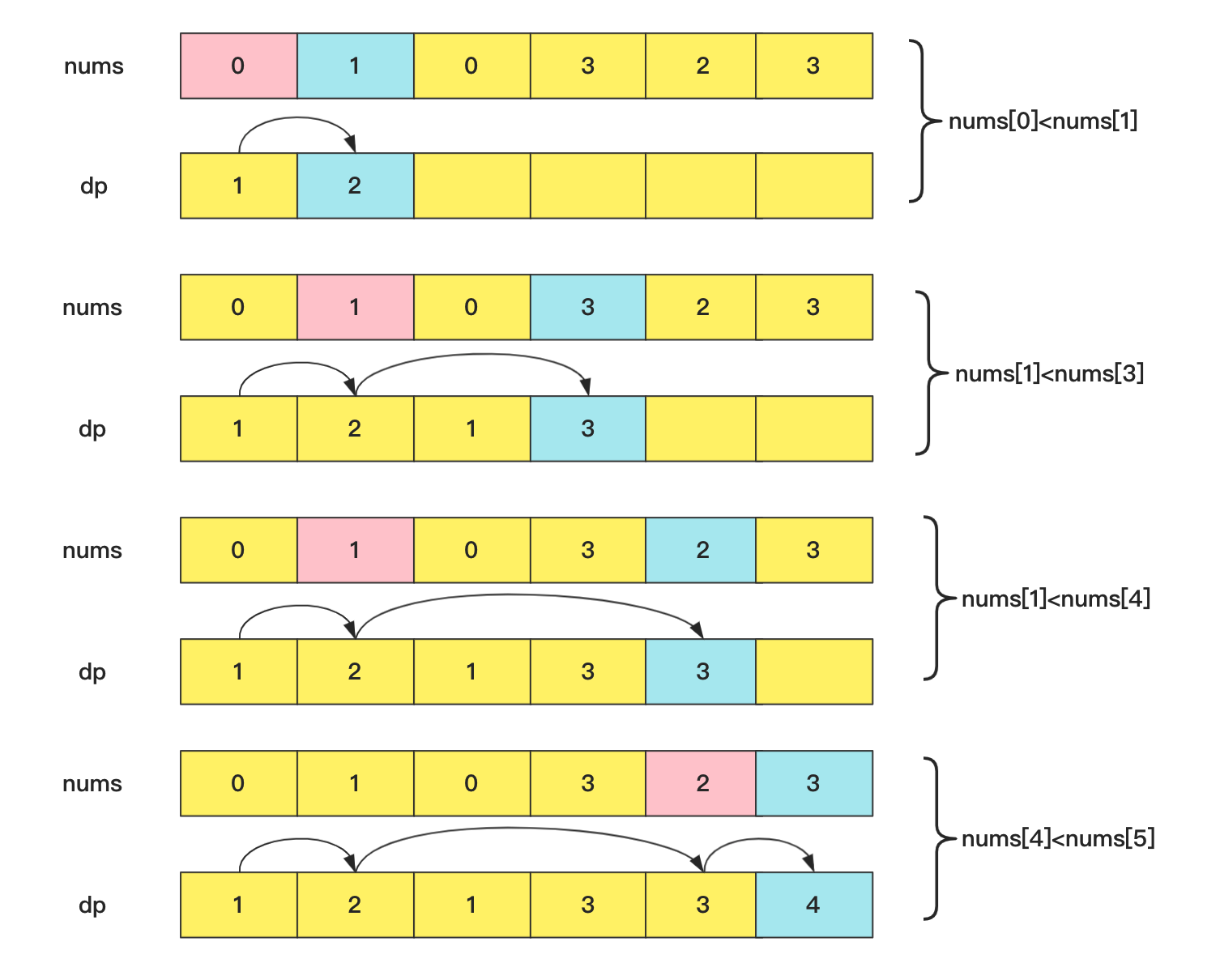
实现代码为:
class Solution {
public int lengthOfLIS(int[] nums) {
int dp[]=new int[nums.length];
int maxLen=1;
dp[0]=1;
for(int i=1;i<nums.length;i++){
int max=0;//统计前面 末尾数字比自己小 最长递增子串
for(int j=0;j<i;j++){//枚举
//结尾数字小于当前数字 并且长度大于记录的最长
if(nums[j]<nums[i]&&dp[j]>max){
max=dp[j];
}
}
dp[i]=max+1;//前面最长 加上自己
if(maxLen<dp[i])
maxLen=dp[i];
}
return maxLen;
}
}
不过这道题还有一个优化,可以优化成O(nlogn)的时间复杂度。
我们用dp记录以 nums[i] 结尾的最长子序列长度,纵观全局,我们希望在长度一致的情况下末尾的值能够尽量的小!
例如 2,3,9,5 …… 在前面最长的长度为3 我们愿意抛弃2,3,9 而全部使用2,3,5 。也就是对于一个值,我们希望这个值能更新以它为结尾的最长的序列的末尾值。
如果这个值更新不了最长的序列,那就尝试更新第二长的末尾值以防待用。例如 2,3,9,5,4,5 这个序列2,3,5更新2,3,9;然后2,3,4更新2,3,5 为最长的2,3,4,5做铺垫。
而这个思路的核心就是维护一个lenth[]数组,length[i]表示长度为i的子序列末尾最小值,因为我们每次顺序增加一个长度说明这个值比前面的都大(做了充分比较),所以这个数组也是个递增的,递增,那么在锁定位置更新最大长度序列尾值的时候可以使用二分法优化。
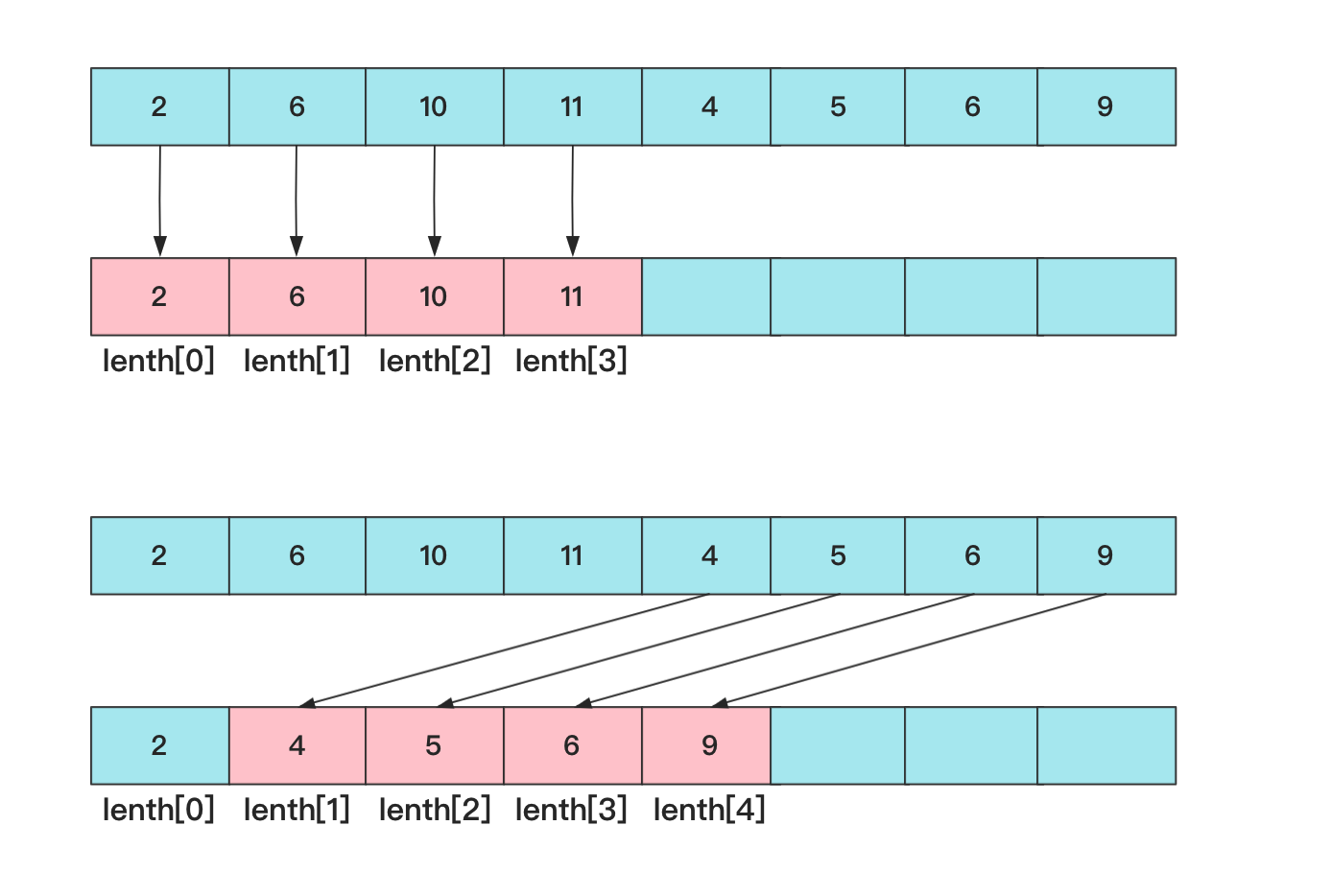
实现代码为:
class Solution {
public int lengthOfLIS(int[] nums) {
int length[]=new int[nums.length];
int len=1;
length[0]=nums[0];
for(int i=1;i<nums.length;i++){
int left=0,right=len;
while (left<right){
int mid=left+(right-left)/2;
if(length[mid]<nums[i]){
left=mid+1;
}else {
right=mid;
}
}
length[left]=nums[i];
if(right==len)
len++;
}
return len;
}
}
最长公共子序列
最长公共子序列也成为LCS.出现频率非常高!
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
拿b c d d e和 a c e e d e举例,其的公共子串为c d e。如果使用暴力,复杂度太高会直接超时,就需要使用动态规划。两个字符串匹配,我们设立二维dp[][]数组,dp[i][j]表示text1串第i个结尾,text2串第j个结尾的最长公共子串的长度。
这里核心就是要搞懂状态转移,分析dp[i][j]的转换情况,当到达i,j时候:
如果text1[i]==text2[j],因为两个元素都在最末尾的位置,所以一定可以匹配成功,换句话说,这个位置的邻居dp值不可能大于他(最多相等)。所以这个时候就是dp[i][j]=dp[i-1][j-1] +1;
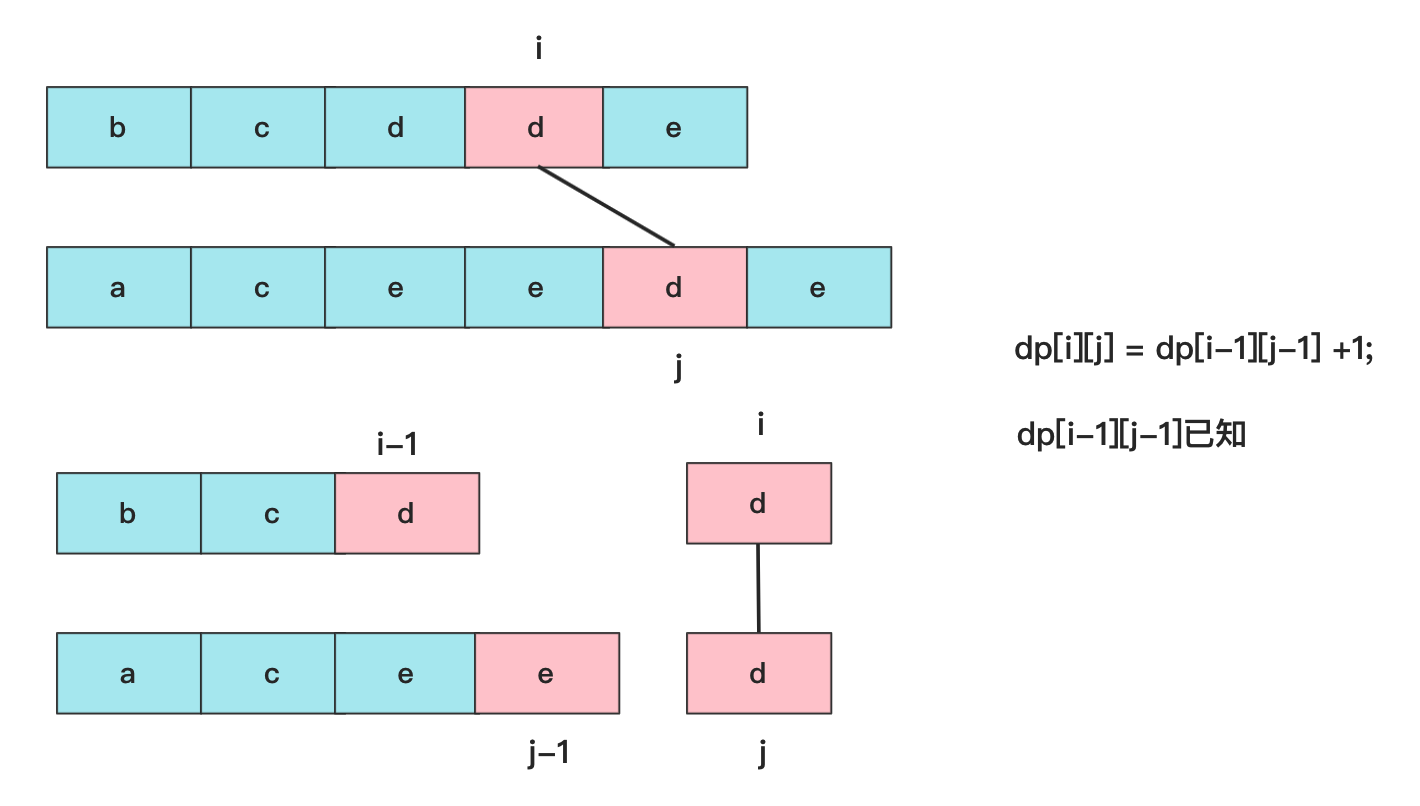
如果text1[i]!=text2[j],就有两种可能性,我们知道的邻居有dp[i-1][j],dp[i][j-1],很多人还会想到dp[i-1][j-1]这个一定比前两个小于等于,因为就是前面两个子范围嘛!所以这时就相当于末尾匹配不成,就要看看邻居能匹配的最大值啦,此时dp[i][j]=max(dp[i][j-1],dp[i-1][j])。
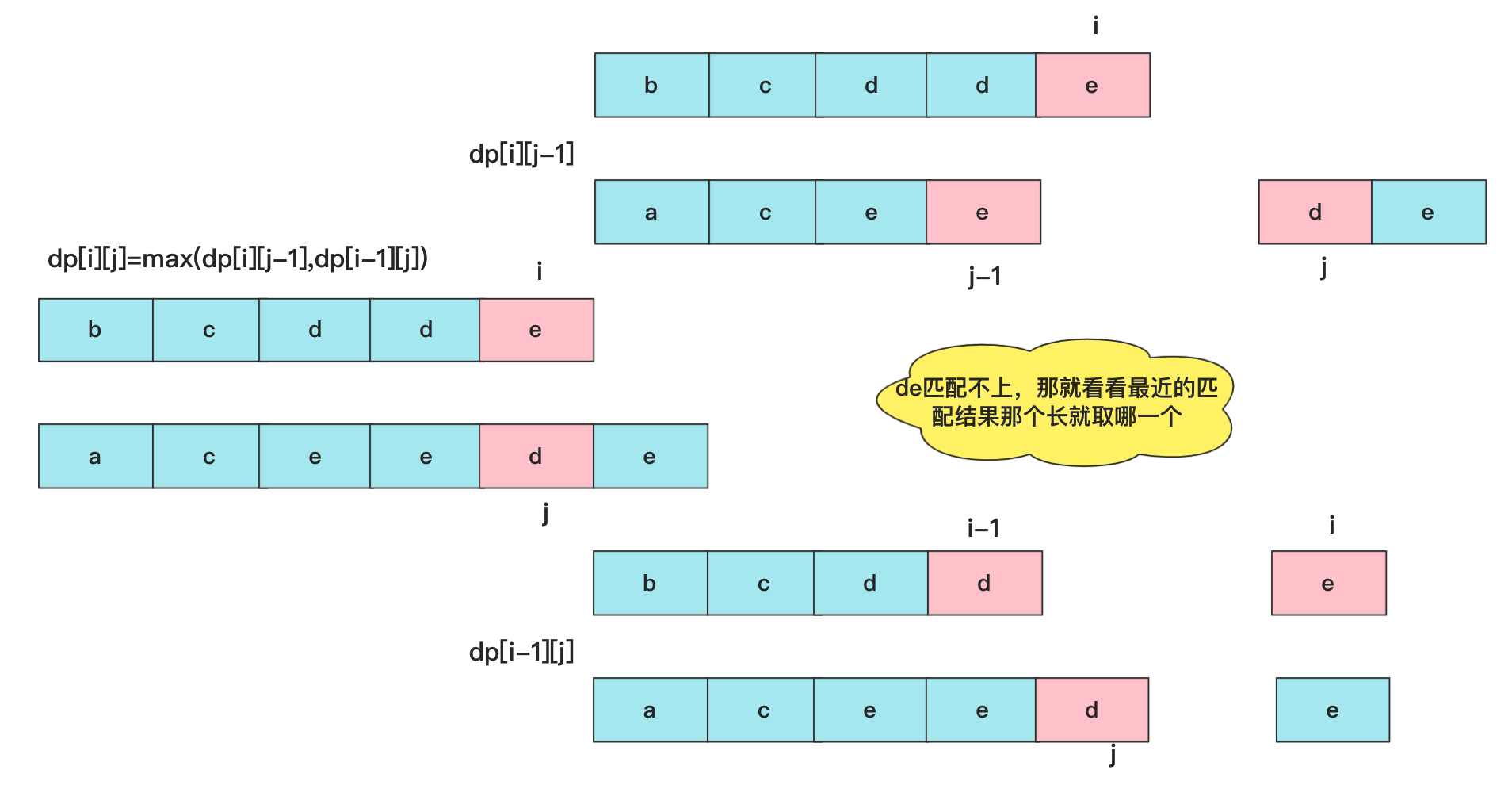
所以整个状态转移方程为:
dp[i][j] = dp[i-1][j-1] + 1 //text1[i]==text2[j]时
dp[i][j] = max(dp[i][j-1],dp[i-1][j]) //text1[i]!=text2[j]时
实现代码为:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
char ch1[]=text1.toCharArray();
char ch2[]=text2.toCharArray();
int dp[][]=new int[ch1.length+1][ch2.length+1];
for(int i=0;i<ch1.length;i++)
{
for(int j=0;j<ch2.length;j++)
{
if(ch1[i]==ch2[j])
{
dp[i+1][j+1]=dp[i][j]+1;
}
else
dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j]);
}
}
return dp[ch1.length][ch2.length];
}
}
最长公共子串
给定两个字符串str1和str2,输出两个字符串的最长公共子串。
例如 abceef 和a2b2cee3f的最长公共子串就是cee。公共子串是两个串中最长连续的相同部分。
如何分析呢? 和上面最长公共子序列的分析方式相似,要进行动态规划匹配,并且逻辑上处理更简单,只要当前i,j不匹配那么dp值就为0,如果可以匹配那么就变成dp[i-1][j-1] + 1
核心的状态转移方程为:
dp[i][j] = dp[i-1][j-1] + 1 //text1[i]==text2[j]时
dp[i][j] = 0 //text1[i]!=text2[j]时
这里代码和上面很相似就不写啦,但是有个问题有的会让你输出最长字符串之类,你要记得用一些变量存储值。
不同子序列
不同子序列也会出现,并且有些难度,前面这篇不同子序列问题分析讲的大家可以看看。
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
示例 :
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^
分析:
这个问题其实就是上面有几个pat的变形拓展,其基本思想其实是一致的,上面那题问的是有几个pat,固定、且很短。但这里面t串的长度不固定,所以处理上就要使用数组来处理而不能直接if else。
这题的思路肯定也是动态规划dp了,dp[j]的意思就是t串中[0,j-1]长字符在s中能够匹配的数量(当然这个值从前往后是动态变化的),数组大小为dp[t.length+1]。在遍历s串的每一个元素都要和t串中所有元素进行对比看看是否相等,如果s串枚举到的这个串和t串中的第j个相等。那么dp[j+1]+=dp[j]。 你可能会问为啥是dp[j+1],因为第一个元素匹配到需要将数量+1,而这里为了避免这样的判断我们将dp[0]=1,这样t串的每个元素都能正常的操作。
但是有一点需要注意的就是在遍历s串中第i个字母的时候,遍历t串比较不能从左向右而必须从右向左。因为在遍历s串的第i个字符在枚举dp数组时候要求此刻数据是相对静止的叠加(即同一层次不能产生影响),而从左往右进行遇到相同字符会对后面的值产生影响。区别的话可以参考下图这个例子:
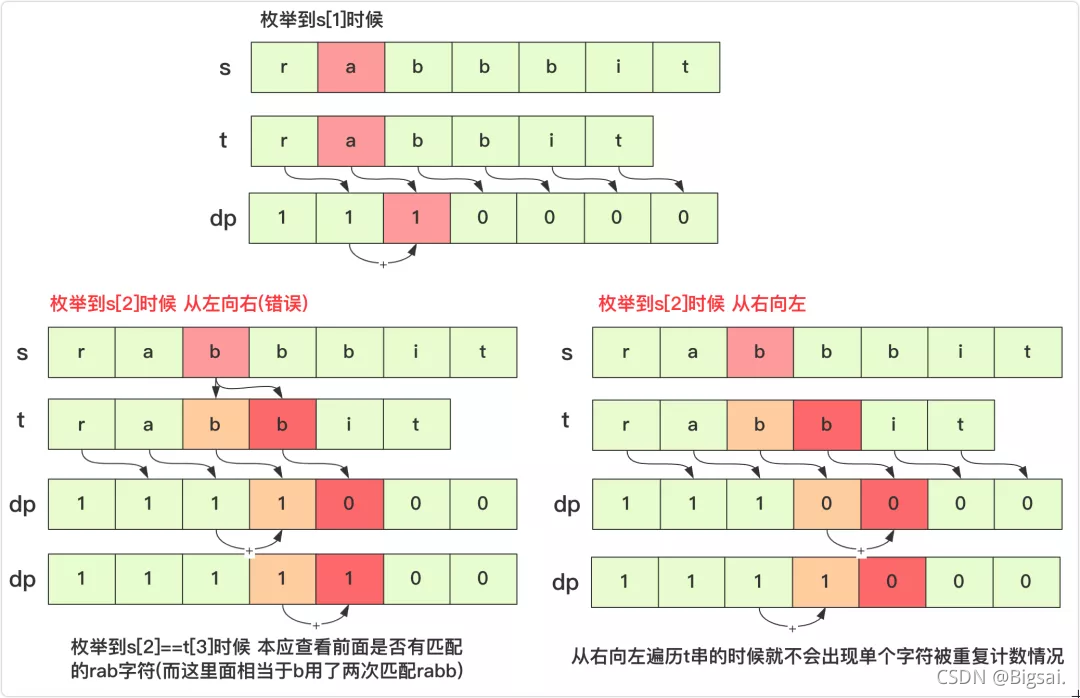
实现的代码为:
class Solution {
public int numDistinct(String s, String t) {
char s1[]=s.toCharArray();
char t1[]=t.toCharArray();
int dp[]=new int[t1.length+1];
dp[0]=1;//用来叠加
for(int i=0;i<s1.length;i++)
{
for(int j=t1.length-1;j>=0;j--)
{
if(t1[j]==s1[i])
{
dp[j+1]+=dp[j];
}
}
}
return dp[t1.length];
}
}
结语
至此,简单的动态规划算是分享完了。
大部分简单动态规划还是有套路的,你看到一些数组问题、字符串问题很有可能就暗藏动态规划。动态规划的套路跟递归有点点相似,主要是找到状态转移方程,有时候考虑问题不能一步想的太多(想太多可能就把自己绕进去了),而动态规划就是要大家对数值上下转换计算需要了解其中关系。
对于复杂dp问题或者很多套一层壳确实很难看出来,但是掌握上面的常见dp问题和背包问题,就可以解决大部分动态规划问题啦(毕竟咱们不是搞竞赛遇到的还是偏简单或者中等难度的)。

原创不易,求个三连!最近,我把自己的原创文章整理成一本数据结构与算法pdf,一共218页会定期更新维护,关注我的公众号回复【666】即可领取,欢迎点击下面名片👇🏻👇🏻👇🏻关注。