问题引入 - 什么是斐波那契数列?
斐波那契数列中,第n项为n-1和n-2项之和
1,1,2,3,5,8,13,21,34,55……
这个数列非常经典,经常用于编程语言初学者的练习
接下来让我们用非递归和递归两种方式来实现这个数列
并了解两种方法的优缺点!
1.非递归方法(迭代)
什么是迭代?
迭代其实和循环的意义差不多(个人理解)
我们计算斐波那契数列的时候,需要从第一项和第二项1、1开始计算
没后一项数字都是前两项数字之和
这样我们就可以利用循环,从第一项开始不断相加,再使其中一个加数等于得到的和
以此迭代,就能得到我们需要的第n个数字
代码实现
#include<stdio.h>
//非递归
int fo1(int a)
{
int tmp = 0;
int num1 = 1;
int num2 =1;
if (a < 3) //前两项都为1
{
return 1;
}
else//从第三项开始迭代
{
for (int i = 0; i <= a - 3; i++)
{
tmp = num1 + num2;
num1 = num2;
num2 = tmp;
}
return tmp;
}
}
int main()
{
int a,b = 0;
scanf("%d", &a);
b=fo1(a);
printf("%d\n", b);
return 0;
}
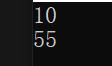
结果如图:
迭代的缺点
这种方法有个缺点,即数字很大的时候,容易栈溢出
如果栈溢出没有影响,迭代的方法就非常适合
比如:
题目规定了不考虑栈溢出
题目设定了数字范围
2.递归
使用递归的基本方法,和迭代其实是一样的
最大的不同是:递归的核心是函数自己调用自己
代码实现
#include<stdio.h>
//递归
int fo2(int a)
{
if ((a == 1) || (a == 2))
{
return 1;
}
else
{
return (fo2(a - 1) )+( fo2(a- 2));//n-1和n-2项
}
}
int main()
{
int a,b = 0;
scanf("%d", &a);
b=fo2(a);
printf("%d\n", b);
return 0;
}
最终执行的效果是一样的
递归的缺点
递归的实现方式是函数不停地自己调用自己

如图所示,当我们需要第50个斐波那契数列中的数时
函数需要从50开始,49、48,再48、47……
这么一直递归到第3个斐波那契列数,才能逐级返回每项的数字,得出最终答案
这就大大增加了程序运行的时间!
你可能会发现程序依旧很快运行完了,那是因为现在电脑cpu的运行速度已经非常快了
但在有运行时间要求的题目中,这样浪费时间是万万不可的
总结
递归和迭代两种方法各有优劣,我们需要在具体情境中选择是使用递归还是迭代
计算斐波那契数列只是这其中的一部分
如果这篇博客对你有帮助,那就点个赞再走吧!