[数据结构与算法]动态规划 背包问题 模板

背包九讲模板（部分）

背包九讲pdf资源
pdf下载

题目

题目链接第1-10题

01背包

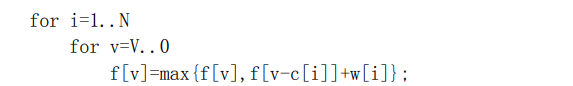
 cin>>n>>m;
 for(int i=0;i<n;++i){
        cin>>v>>w;
        for(int j=m;j>=v;--j){
            f[j]=max(f[j],f[j-v]+w);
        }
    }

完全背包

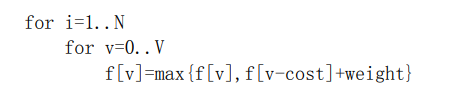
    cin>>n>>m;
    for(int i=0;i<n;++i){
        cin>>v>>w;
        for(int j=v;j<=m;++j){
            f[j]=max(f[j],f[j-v]+w);
        }
    }

多重背包

01背包和完全背包可以看作特殊的多重背包，多重背包的优化是相对较难的一类背包问题.

多重背包直接求解

for(int i=0;i<n;++i){
    cin>>v>>w>>s;
    for(int j=m;j>=v;--j){
        for(int k=1;k<=s && k*v<=j;++k){
            dp[j]=max(dp[j],dp[j-k*v]+k*w);
        }
    }
}

二进制优化背包问题

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=2010;
int n,m;
int dp[maxn];

int main(void){
    cin>>n>>m;
    int v,w,s;
    for(int i=0;i<n;++i){
        cin>>v>>w>>s;
        if(v*s>=m){
        	//完全背包
            for(int j=v;j<=m;++j){
                dp[j]=max(dp[j],dp[j-v]+w);
            }
        }else{
            int k=1;
            while(k<s){
                int kw=k*w,kv=k*v;
                //01背包
                for(int j=m;j>=kv;--j)
                    dp[j]=max(dp[j],dp[j-kv]+kw);
                s-=k;
                k=2*k;
            }
            if(s>0){
                k=s;
                int kw=k*w,kv=k*v;
                //01背包
                for(int j=m;j>=kv;--j)
                    dp[j]=max(dp[j],dp[j-kv]+kw);
            }
        }
    }
    cout<<dp[m]<<endl;
}

单调队列优化背包问题

详解参看
f[i,j]代表前i个物品，在体积限制j的情况下，能够取得的最大重量如何使用单调队列来优化？首先可以看到对于每一个j来说，如果j%v的余数相同，那么他们就可以使用单调队列求最近s个数中的最大值，对于每一个余数，可以使用一个单调队列优化到O(1)。这中间有一个小问题，就是每一个子状态f[i-1,j-xv]的后缀不同，有的+w,有的+2w,…+sw，但是他们有一个统一的规律，就是离j越近，后缀越小，距离0越大，后缀越大，所以为了对比他们之间的大小关系，可以在后面统一减去一个kw放到max的外面去，k=(j-(j%v))/v,这样得到

f[i,j]=max{f[i-1,j]-k*w,f[i-1,j-v]-(k-1)*w,f[i-1,j-2*v]-(k-2)*w,....,f[i-1][j-sv]-(k-s)*w}  +  k*w
f[i,j-v]=max{f[i-1,j-v]-(k-1)*w,f[i-1][j-2*v]-(k-2)*w,...,f[i-1][j-sv]-(k-s)*w,f[i-1][j-(s+1)v]-(k-s-1)*w}  +  k*w

上面两式中

f[i-1,j-v]-(k-1)*w,f[i-1,j-2*v]-(k-2)*w,....,f[i-1][j-sv]-(k-s)*w

部分已经达成了一致，可以使用单调队列了,其中每一项可以写作f[i-1,j-xv]-(k-x)*w，1<=x<=s

#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=20010;
int N,V,f[maxn],g[maxn],q[maxn],v,w,s;

int main(void){
    cin>>N>>V;
    for(int i=0;i<N;++i){
        cin>>v>>w>>s;
        memcpy(g,f,sizeof f);
        for(int j=0;j<v;++j){
            int hh=0,tt=-1;  //根据余数j，每一个余数重置一次单调队列
            for(int k=j;k<=V;k+=v){
                if(hh<=tt && k-q[hh]>s*v) ++hh;  //第一步，排除非法的选择，也就是个数最大选择s个
                if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);  //更新f[k],这个地方必须放在第二步
                while(hh<=tt && g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w) --tt; //第三步，去除f[i-1,j-xv]-(k-x)*w较小的值
                q[++tt]=k;
            }
        }
    }
    cout<<f[V]<<endl;
}

混合背包

求解方式如下图，分开求解

二维背包

二维背包一般情况下只是一维01背包的扩展，所以求解比较简单，优化方式参见一维的01背包优化方式

分组背包

分组背包是多重背包的泛化形式，多重背包可以看成分组背包的特例。分组背包最关键的地方就在于将每个组看作一个物品，然后就可以变成01背包问题，对于每组内的物品，在最内层加一个循环

模板题目

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=110;
int n,m,s[maxn],v[maxn][maxn],w[maxn][maxn],dp[maxn];

int main(void){
    cin>>n>>m;
    for(int i=1;i<=n;++i){
        cin>>s[i];
        for(int j=1;j<=s[i];++j){
            cin>>v[i][j]>>w[i][j];
        }
    }
    for(int i=1;i<=n;++i){  //遍历每一组
        for(int j=m;j>=0;--j){  //遍历花费
            for(int k=1;k<=s[i];++k){  //遍历组内物品
                if(j>=v[i][k]) dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<dp[m]<<endl;
}

其中，如果有一组里面有多个可选物品的情况，可以枚举所有情况，一般是2^k种，然后可以转变成分组背包问题，例题

有依赖的背包问题

例题 题解

求解方式很明确，使用树形dp，其中最关键的就是定于状态是什么？一般定义dp[i][j]，i是子树的根节点，j是花费。对于每一颗子树和他的儿子们，先递归求出儿子们的状态，然后将他们看作是一个分组背包问题。每一个儿子代表一个物品组，物品组的个数就是他的儿子的状态数量。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=110;
int n,m;
int v[maxn],w[maxn],p[maxn],dp[maxn][maxn];
//dp[i][j]表示选择物品i且体积为j时的最大价值,也是以i为根的整颗子树最大价值
int e[maxn],ne[maxn],h[maxn],idx;

void add_edge(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u){
	//将每个儿子看作一个物品组，物品组总数量就是儿子的数量，每个物品组内物品个数就是最大体积
    for(int i=h[u];i!=-1;i=ne[i]){
        int b=e[i];
        //先对所有的儿子们求出它们的状态
        dfs(b);
		//从大到小遍历体积，要预先留出v[u]
        for(int j=m-v[u];j>=0;--j){
        	//遍历 物品组 内的选择
            for(int k=0;k<=j;++k){
                dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[b][k]);
            }
        }
    }
    //由于u是必须选的，所以对dp[u]进行处理
    for(int i=m-v[u];i>=0;--i) dp[u][i+v[u]]=dp[u][i]+w[u];
    for(int i=0;i<v[u];++i) dp[u][i]=0;
}

int main(void){
    memset(h,-1,sizeof h);
    int root=0;
    cin>>n>>m;
    //建树
    for(int i=1;i<=n;++i){
        cin>>v[i]>>w[i]>>p[i];
        if(p[i]==-1) root=i;
        else add_edge(p[i],i);
    }
    dfs(root);  //树形dp
    cout<<dp[root][m]<<endl;
}