数据结构基础——堆的概念、结构及应用

1.堆的概念

堆就是以二叉树的顺序存储方式来存储元素，同时又要满足父亲结点存储数据都要大于儿子结点存储数据（也可以是父亲结点数据都要小于儿子结点数据）的一种数据结构。堆只有两种即大堆和小堆，大堆就是父亲结点数据大于儿子结点数据，小堆则反之。

堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

用图画展示就如下图所示：
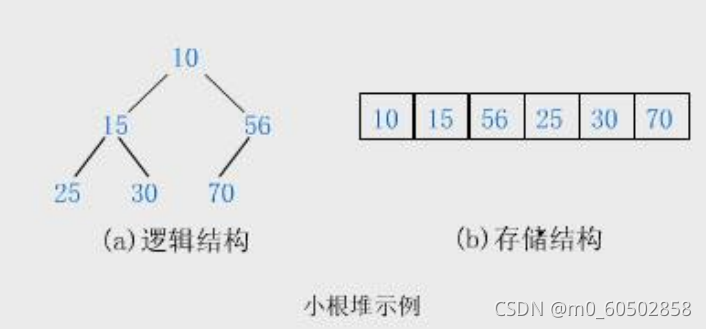
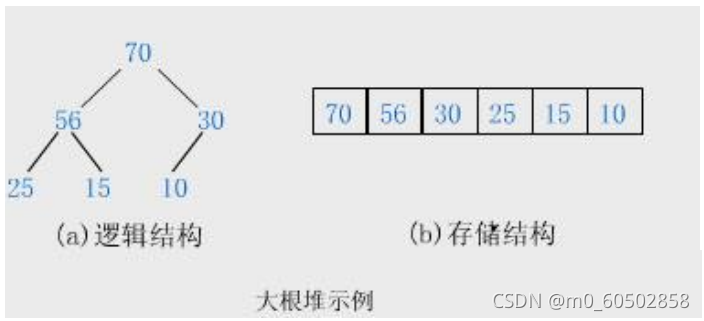
在这里插入图片描述

2.堆这种数据结构的代码实现

了解了堆的概念之后，我们要实际写出一个堆来，先写个小堆为例。
物理结构是用一个数组来存储数据，先定义一个动态增长的数组来。

typedef int Datatype;
typedef struct                                          
{                
	Datatype* a;
	int size;
	int capacity;
}heap;
 //这就是堆的基本形式了，然后再按照完全二叉数的逻辑形式插入数据

在测试的源文件中创建一个堆

heap hp;    //之后就可以写各种堆的功能函数来操作堆了，都是通过传堆的地址过去来操作的

//在头文件中就先声明跟堆有关的各种接口函数                       
void heapinit(heap* hp);   //堆的初始化
void heapdestroy(heap* hp); //堆的销毁
void heappush(heap* hp, Datatype x);  //数据进堆
void heappop(heap* hp);   //数据出堆
void heapadjustdown(int* a, int n, int x);//向下调整
void heapadjustup(int* a, int n, int x); //向上调整
void swap(int* a, int* b);   //交换两个数值
void print(heap* hp);   //打印堆的数据
bool heapEmpty(heap* hp); //判断堆是否时空堆
int heapSize(heap* hp);  //计算堆的数据元素个数
Datatype heaptop(heap* hp); //获得堆顶的数据

然后在另一个源文件中定义这些函数，并加以详细说明。

void heapinit(heap* hp)
{
   assert(hp);
	hp->a = NULL;  //堆的初始化，此时堆中没有数据                
	hp->capacity = hp->size = 0;
}

//往堆中加入数据，物理结构上是不断地在数组尾部加入数据，但加入数据后就要调整数据维持一个小堆或大堆的逻辑结构,要有一个向上调整的函数。如下图所示
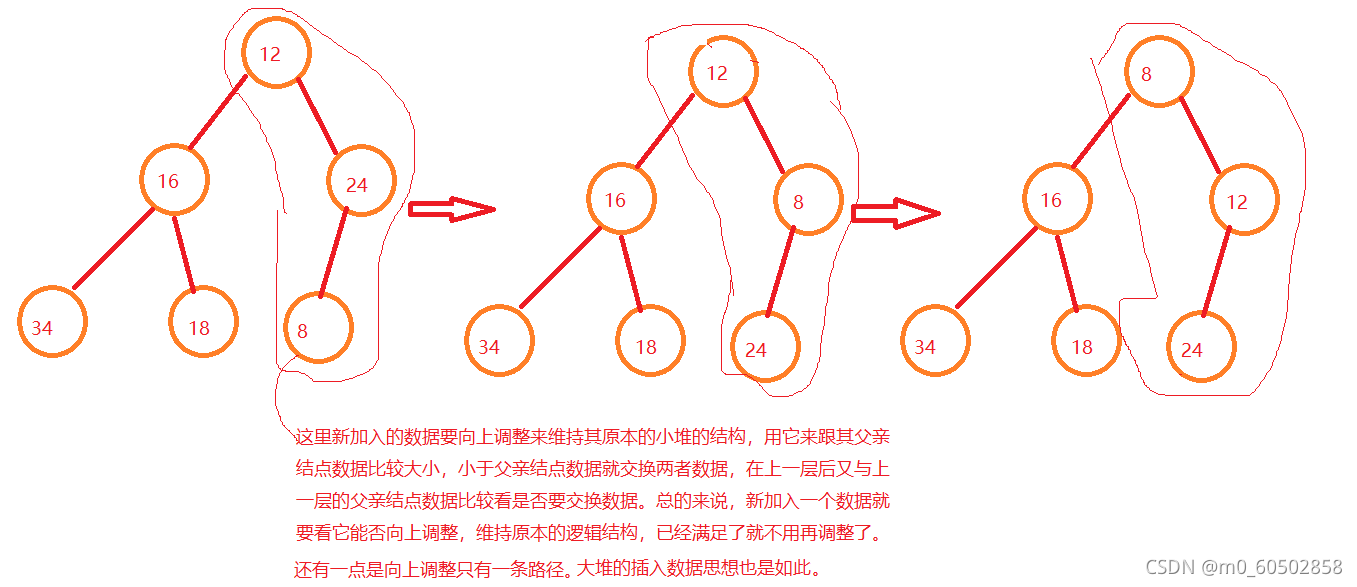
在这里插入图片描述

void heappush(heap* hp, Datatype x)
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newcapacity = (hp->capacity == 0) ? 4 : 2 * hp->capacity;
		Datatype* tem = (Datatype*)realloc(hp->a, newcapacity * sizeof(Datatype));
		if (tem == NULL)   //这里就是动态数组的常规检查容量问题
		{
			printf("realloc failed\n");
			exit(-1);
		}
		hp->a = tem;
		hp->capacity = newcapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	heapadjustup(hp->a, hp->size, hp->size - 1);
}
void heapadjustup(int* a, int n, int child)
{    //向上调整的函数
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])               //大堆向上调整，用大于号方便识别  小堆就用小于号
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}

另一个主要的函数是堆的删除数据的函数，规定堆只能从根节点删除数据，把堆尾部的数据与根节点的数据交换，然后删除被换到堆尾部那个原先在根节点的数据，让刚换到根结点的数据向下调整维持堆原先的大堆或小堆结构。

void heappop(heap* hp)
{
	assert(hp);
	if (heapEmpty(hp))    //判断是否还有数据可以删除
	{
		printf("没有数据可删\n");
		return;
	}
	swap(&hp->a[0], &hp->a[hp->size - 1]);   //交换根结点和最后一个叶节点数据
	hp->size--;
	heapadjustdown(hp->a, hp->size, 0);  //向下调整函数
}

向下调整就跟向上调整有区别了，从根结点开始向下可能有不同的路径，我们要维持住小堆则最小的数在堆顶，大堆则最大的数在堆顶。具体看下图所示
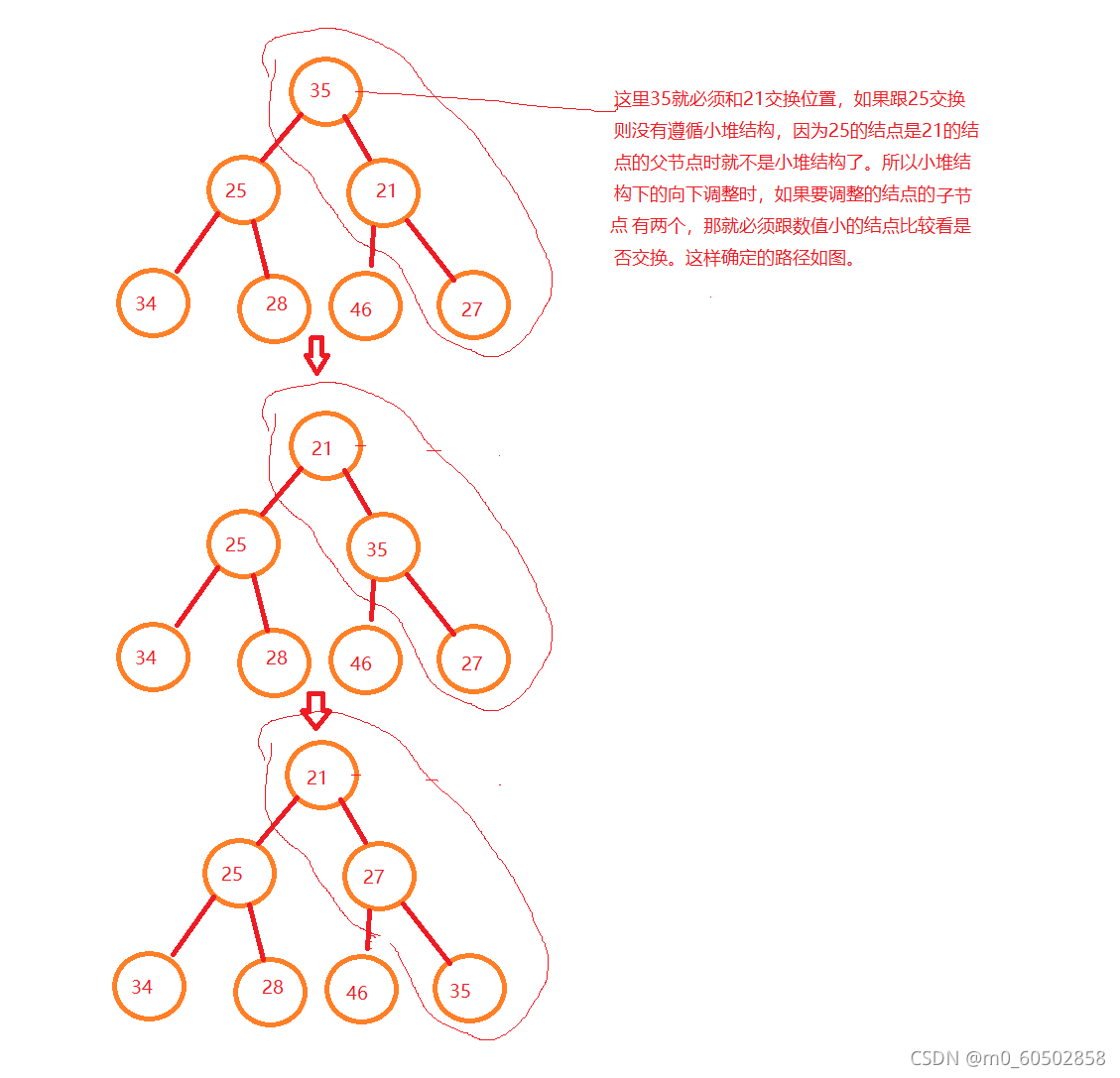
在这里插入图片描述

//向下调整函数的实现
void heapadjustdown(int* a, int n, int parent)
{
	int  child = 2 * parent + 1;
	while (child < n)    //判断有没有到叶子结点
	{
		if (child + 1 < n && a[child + 1] < a[child])   //大堆向下调整，用大于号方便识别  小堆就用小于号
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(a + parent, a + child);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

后面其它函数的实现

void swap(int* a, int* b)   //交换两个位置的数据
{
	int tem = *a;
	*a = *b;
	*b = tem;
}
void print(heap* hp)    //在屏幕上打印堆的数据
{
	assert(hp);
	assert(hp->a);
	for (int i = 0; i < hp->size; i++)
		printf("%d ", hp->a[i]);
	printf("\n");
}
bool heapEmpty(heap* hp)    //判断堆是否为空，空就返回真，否则返回假
{
	assert(hp);
	return hp->size == 0;
}
int heapSize(heap* hp)   //返回堆的数据个数
{
	assert(hp);
	return hp->size;
}
Datatype heaptop(heap* hp)   /获得堆顶的数据
{  
	assert(hp);
	assert(!heapEmpty(hp));
	return hp->a[0];
}
void heapdestroy(heap* hp)   //最红销毁堆
{
	assert(hp);
	assert(hp->a);
	free(hp->a);
	hp->capacity = hp->size = 0;
}

3.堆在排序算法上的应用

用堆这种数据结构来找一组数据中最大的或者最小的几个数据是一种比较高效的算法，小堆就是比较大的数据都在堆的下面，如果要找出N个数中最大的K个数，我们可以先用N个数中的K个数建一个小堆，最小的数在堆顶，拿其余N-K个数依次与堆顶数据比较，大于堆顶数据，就拿它更新堆顶数据，在向下调整，比较完这N-K个数后，堆中的K个数就是这N个数中最大的K个数。同理在大堆中最大的数在堆顶，较小的数在堆下面，以同样的规律，比较数据，如果小于堆顶数据就更新堆顶数据，最后留在堆中的K个数就是N个数中最小的数据。
这里来找一下N个数中最大的K个数。

void printTok(int* a, int n, int k)；//找最大的K个数的函数声明
void testTok()     //找出N个数中最大的K个数的函数测试  数据的准备
{
 int N = 10000, k = 10;   
 int* a = (int*)malloc(sizeof(int) * N);
 if (a == NULL)
 {
 	printf("malloc fail\n");
 	exit(-1);
 }
 srand((size_t)time(0));
 for (int i = 0; i < N; i++)
 {
 	a[i] = rand() % 10000;
 }
 a[24] = 10000 + 5;  //事先准备10个最大的数，测试能不能在10000个数中找出它们
 a[56] = 10000 + 7;
 a[78] = 10000 + 6;
 a[5] = 10000 + 12;
 a[68] = 10000 + 9;
 a[355] = 10000 + 15;
 a[789] = 10000 + 1;
 a[865] = 10000 + 8;
 a[7900] = 10000 + 4;
 a[5846] = 10000 + 3;
 printTok(a, N, 10);
 free(a);
}
void printTok(int* a, int n, int k)   //找最大的K个数的函数实现
{
 int i;
 heap hp;
 heapinit(&hp);
 for (i = 0; i < k; i++)
 {
 	heappush(&hp, a[i]);
 }
 for (i = k; i < n; i++)
 {
 	if (a[i] > heaptop(&hp))
 	{
 		hp.a[0] = a[i];
 		heapadjustdown(hp.a, hp.size, 0);
 	}
 }
 print(&hp);
 heapdestroy(&hp);
}