依然跟随@川川菜鸟?打卡第二天
文章目录
结论:综上,最优解:x1 = 4 ,x2 = 2 ;最优值:340?
结果2:最优解:x1 = 4 ,x2 = 2 ;最优值:340?
结果3:最优解:x1 = 4 ,x2 = 2 ;最优值:340?
一、本次问题
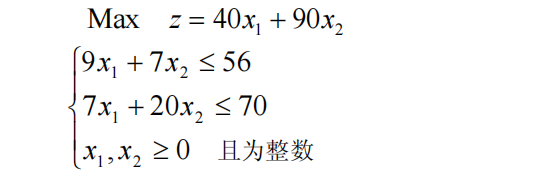
1.利用第一天所学知识求解:
代码如下:
%打卡第一天
clear all
clc
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%不等式约束条件左边约束
b=[56 70];%不等式约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;0];%没有下限
ub=[inf;inf];%没有上限
[x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);
x %获取对应x1,x2
best=c*x%计算最优值2.本题理解:
由于问题要求求解结果都为整数,所以第一问结果错误,那么我们该如何求得想要得整数解呢?
(1)分支界定法
背景:
今天利用matlab来实现求解完全整数规划问题的分支定界法。这里求解的模型为目标函数最小化模型:
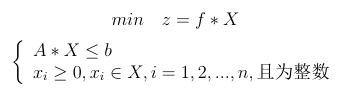
基本理论(解题步骤):
- 分支定界法:用以求解整数规划问题的一种方法。
- 求解步骤:
首先我们规定求解的整数规划问题为A,相应的线性规划问题为B
- 对问题B进行求解
1. 若B无可行解,则A也无可行解,停止计算
2. 若B有最优解,且符合整数条件,该最优解为A的最优解,停止计算
3. 若B有最优解,但不符合整数条件,记它的目标函数值为z*,作为最优值的下界 - 找出问题A的一个整数可行解,其目标函数值作为最优解的上界
- 进行迭代
- 分支,在B的最优解中任选一个不符合整数条件的变量x j x_jxj?,其值为b j b_jbj?,构造两个约束条件,
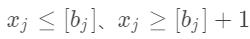 ,分别加入到问题B中,形成两个子问题B1?、B2?。不考虑整数条件求解这两个子问题。即分支
,分别加入到问题B中,形成两个子问题B1?、B2?。不考虑整数条件求解这两个子问题。即分支 - 定界。对每个后继问题表明其求解的结果,与其他问题进行比较,将最优目标函数值最小者(不包括问题B)作为新的下界,在已符合整数条件的各分支中,找出目标函数值最小者作为新的上界。
- 剪枝,将目标函数值不在上界、下界中的分支剪去
- 重复1 2 3,直到得到最优解
注意事项:在对两分支进行分解时,优先选择目标函数值最小的分支进行分解。
- 分支,在B的最优解中任选一个不符合整数条件的变量x j x_jxj?,其值为b j b_jbj?,构造两个约束条件,
分支定界法中,通过定界进而进行剪枝,对分支进行了筛选,使我们仅在一部分可行解中寻求最优解,而不是全部穷举出来再寻找,其求解效率更高。
求解实现1:
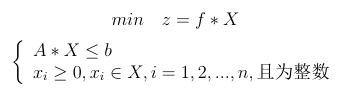
linprog函数及其参数的意义请看建模学习打卡第一天_菜菜笨小孩的博客-CSDN博客
简单介绍下,首先MATLAB中求解的是目标函数是最小值的问题,但如果我们的目标函数是求最大值,可以通过对目标函数中每一项中乘以-1,将求最大值问题转化为求最小值问题;A,b分别为不等式约束中的系数矩阵。Aeq和beq分别为等式约束中的系数矩阵,lb,和ub分别为每个变量的上下区间;最后c为目标函数中各变量的系数矩阵。
1.第一步
根据上面给出的结果,知道结果不符合题意。
于是我们可以暂定z的上限(最大值)为356,又因为当x1,x2全为0时,z也为0,所以可以暂定z的范围为 0<= z <= 356;并且将对x1值的范围问题定为问题A,将对x2值的范围问题定为B
2.第二步
首先,我们对A问题进行分支,改变x1的约束条件,不改变x2的约束条件,即对x1分支得两个子集
x1 =<[4.8092] = 4 , x1 >= [4.8092] +1 = 5约束条件变为:
9*x1+7*x2<=56
7*x1+20*x2<=70
0<x1<4或x1>5 x2>0先对0<x1<4求解??代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;0];%下限依然都为0
ub=[4;inf];%x1上限为4,x2没有上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果为:此时的最优解 x1=4 , x2=2.1 ; 最优值为 349。也不符合题意,所以舍

再对 x1 > 5求解 代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[5;0];% x1的下限变成5,x2下限依然都为0
ub=[inf;inf];%x1,x2没有上限
1
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果为:此时的最优解 x1=5?, x2=1.5714?; 最优值为 341.4286。也不符合题意,所以舍

3.第三步
通过第二部对问题A的分支,我们可以进一步暂定 z 的范围为 0<= z <= 249,又因为第二步中只有x2的为小数,因此我们也就对问题B x2的范围进行限定为 (同上) :
0=<x2<[2.1]=2,x2>[2.1]+1=3
此时约束条件:
9*x1+7*x2<=56
7*x1+20*x2<=70
0<=x1<=4 2>x2>0 或 x2>3
先对约束条件 0<=x1<=4,0<=x2<=2求解? 代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;0];%下限依然都为0
ub=[4;2];%x1上限为4,x2上限为2
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果:此时的最优解 x1=4?, x2=2?; 最优值为 340。符合题意,所以暂时留着

?再对约束条件 0<=x1<=4,x2>=3求解? 代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;3];% x1下限依然都为0,x2下限为3
ub=[4;inf];%x1上限为4,x2无上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果:此时的最优解 x1=1.4286?, x2=3?; 最优值为 327.1429。不符合题意,所以舍

4.第四步
通过上前的,我们可以进一步确定z的范围:0<= z <=241,此时我们已对问题A完成了完美分支,接下来我需对问题B再进行分支
根据上面的结果,x2=1.5714为小数,因此我们对B中的x2进行分支。
0=<x2<[1.5714]=1,x2>[1.5714]+1=2
?此时条件约束:
9*x1+7*x2<=56
7*x1+20*x2<=70
x1>=5 1>x2>0 或 x2>2
?先对x1>=5,1>x2>0求解,代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[5;0];% x1下限为5,x2下限为0
ub=[inf;1];%x1无上限,x2上限为1
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值结果为:此时的最优解 x1=5.4444?, x2=1?; 最优值为 307.7778。不符合题意,所以舍

?再对x1>=5,x2>2求解,代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[5;2];% x1下限为5,x2下限为2
ub=[inf;inf];%x1无上限,x2无上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值结果:此时无解

?
?
结论:综上,最优解:x1 = 4 ,x2 = 2 ;最优值:340?
至于结果为负是因为matlab求解线性规划转化为求最小值

求解实现2:

?linprog函数及其参数的意义请看建模学习打卡第一天_菜菜笨小孩的博客-CSDN博客
简单介绍下,首先MATLAB中求解的是目标函数是最小值的问题,但如果我们的目标函数是求最大值,可以通过对目标函数中每一项中乘以-1,将求最大值问题转化为求最小值问题;A,b分别为不等式约束中的系数矩阵。Aeq和beq分别为等式约束中的系数矩阵,lb,和ub分别为每个变量的上下区间;最后c为目标函数中各变量的系数矩阵。
但线性规范有两种比较特殊的情况,即整数规划和0-1整数规划。在之前(不知MATLAB几之前……),MATLAB是不能直接求解这两种规划的,bintprog函数可以用来求0-1整数规划,但求解过程比较麻烦,而且最新版的MATLAB已经遗弃了这个函数,同时提供了一个比较新的、专用于求解整数规划和0-1整数规划的函数——intlinprog。intlinprog的一个原型为:
[x,fval,exitflag]= intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
该函数的使用和linprog函数的使用十分相似,其仅仅在linprog函数的基础上多了一个参数——intcon。在函数intlinprog中,intcon的意义为整数约束变量的位置。在本题中整数变量为x1,x2,所以intcon=[1,2];fval为最优化的值,一般是一个标量,exitflag意为函数的退出标志。
本题代码如下:
clear all
clc
c=[-40 -90];%用目标函数系数来确定
A=[9 7;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
%lb=zeros(2,1);% 生成一个2行1列的全0矩阵,很显示,上面例子中的x,y的最小值为0
%intcon=[1,2];%整数约束变量的位置
%[x,fval,exitflag]=intlinprog(c,intcon,A,b,[],[],lb,[]) %用矩阵lb求不用设置上限
lb=[0;0];%下限依然都为0
ub=[inf;inf];%x1没有上限,x2没有上限
intcon=[1,2];%整数约束变量的位置
[x,fval,exitflag]=intlinprog(c,intcon,A,b,[],[],lb,ub) %此时需要设置上下限结果2:最优解:x1 = 4 ,x2 = 2 ;最优值:340?
至于结果为负是因为matlab求解线性规划转化为求最小值

?求解实现3:
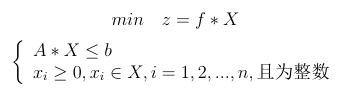
linprog函数及其参数的意义请看建模学习打卡第一天_菜菜笨小孩的博客-CSDN博客
简单介绍下,首先MATLAB中求解的是目标函数是最小值的问题,但如果我们的目标函数是求最大值,可以通过对目标函数中每一项中乘以-1,将求最大值问题转化为求最小值问题;A,b分别为不等式约束中的系数矩阵。Aeq和beq分别为等式约束中的系数矩阵,lb,和ub分别为每个变量的上下区间;最后c为目标函数中各变量的系数矩阵。
1.首先我们需要定义一个满足分支定理条件的函数:
%A,b,c分别对应此题的不等式约束系数矩阵,不等式约束常数向量,目标函数系数向量
%Aeq 等式约束系数矩阵, Beq 等式约束常数向量
%vlb 定义域的下界 vub 定义域的上界
%optXin 每次迭代的最优x optF 每次迭代最优的f值 iter迭代次数
function [xstar, fxstar, flagOut, iter] = BranchBound1(c,A, b, Aeq, Beq, vlb, vub, optXin, optF, iter)
global optX optVal optFlag;%将最优解定义为全局变量
iter = iter + 1;
optX = optXin; optVal = optF;%更新迭代得到的值
% options = optimoptions("linprog", 'Algorithm', 'interior-point-legacy', 'display', 'none');
[x, fit, status] = linprog(c,A, b, Aeq, Beq, vlb, vub, []);
%status返回算法迭代停止原因
%status = 1 算法收敛于解x,即x是线性规划的最优解
if status ~= 1%没有找到最优解,此分支不用继续迭代下去,返回
xstar = x;
fxstar = fit;
flagOut = status;
return;
end
if max(abs(round(x) - x)) > 1e-3%找到的函数最优解仍不是整数解
if fit > optVal %此题求解的是max,此时的函数值大于之前解得的值
xstar = x;
fxstar = fit;
flagOut = -100;
return;
end
else%此时解得的函数解为整数解,此分支求解结束,不再继续向下求解,返回
if fit > optVal %此题求解的是max,此时的函数值大于之前解得的值
xstar = x;
fxstar = fit;
flagOut = -101;
return;
else %解出的值<之前解得的值,先放入全局变量中暂时存放
optVal = fit;
optX = x;
optFlag = status;
xstar = x;
fxstar = fit;
flagOut = status;
return;
end
end
midX = abs(round(x) - x);%得到x对应的小数部分
notIntV = find(midX > 1e-3);%得到非整数的x的索引值,find()函数返回非0的索引值
pXidx = notIntV(1);%得到第一个非整数x的下标索引
tempVlb = vlb;%临时拷贝一份
tempVub = vub;
%fix(x) 函数将x中元素零方向取整
if vub(pXidx) >= fix(x(pXidx)) + 1%原上界大于此时找到的分界的位置值
tempVlb(pXidx) = fix(x(pXidx)) + 1;%将这个分界位置值作为新的下界参数传入,进一步递归
[~, ~, ~] = BranchBound1(c,A, b, Aeq, Beq, tempVlb, vub, optX, optVal, iter + 1);
end
if vlb(pXidx) <= fix(x(pXidx))%原下界小于此时找到的分界的位置值
tempVub(pXidx) = fix(x(pXidx));%将这个分界位置值作为新的上界参数传入,进一步递归
[~, ~, ~] = BranchBound1(c,A, b, Aeq, Beq, vlb, tempVub, optX, optVal, iter + 1);
end
xstar = optX;
fxstar = optVal;
flagOut = optFlag;
end2.调用上面函数对问题进行求解:
%A,b,c分别对应此题的不等式约束系数矩阵,不等式约束常数向量,目标函数系数向量
%Aeq 等式约束系数矩阵, Beq 等式约束常数向量
%lb 定义域的下界 ub 定义域的上界
clear all
clc
A = [9 7;7 20];
b = [56 70];
c = [-40,-90];%标准格式是求min,此题为max,需要转换一下
lb = [0; 0];%x值的初始范围下界
ub=[inf;inf];%x值的初始范围上界
optX = [0; 0];%存放最优解的x,初始迭代点(0,0)
optVal = 0;%最优解
[x, fit, exitF, iter] = BranchBound1(c,A, b,[], [], lb, ub, optX, optVal, 0)结果3:最优解:x1 = 4 ,x2 = 2 ;最优值:340?
至于结果为负是因为matlab求解线性规划转化为求最小值

总结:
综上所述:最优解:x1 = 4 ,x2 = 2 ;最优值:340? 为正解;本次通过学习分支界定法求整数线性规划,学了很长时间,最终功夫不负有心人啊!!如果本文章有错误问题,请大家指出!!感谢!