[数据结构与算法]【图解数据结构】堆 - 基本功能实现、向上调整、向下调整算法

前置知识

堆本质上是一个完全二叉树，但存储结构是一个数组。这个是对堆进行代码编写的核心，要牢牢把握住！

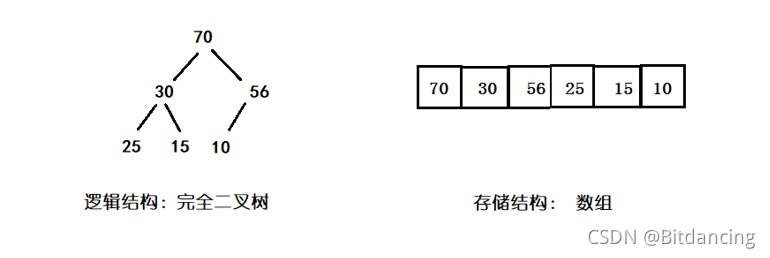
下文代码以大堆为例！

堆结构定义

堆的物理本质是一个数组，就可以像动态顺序表一样进行结构定义。

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size; // 有效元素个数
	int capacity; // 数组长度
}HP;

函数接口

// 堆的初始化
void HeapInit(HP* hp);
// 堆的销毁
void HeapDestroy(HP* hp);
// 堆push数据
void HeapPush(HP* hp, HPDataType x);
// 堆pop堆顶
void HeapPop(HP* hp);
// 获得堆顶数据
HPDataType HeapTop(HP* hp);
// 空堆
bool HeapEmpty(HP* hp);
// 堆大小
int HeapSize(HP* hp);

堆的初始化

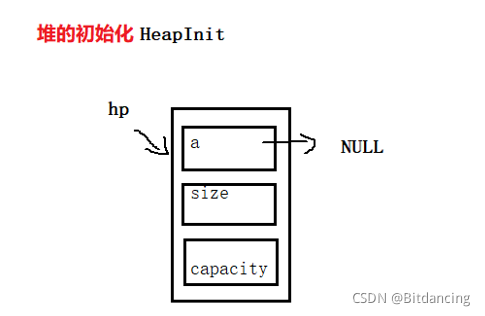
void HeapInit(HP* hp)
{
	assert(hp);

	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

堆的销毁

顺序表空间连续，所以只要free（首地址）就可以。

注意：不能忘记 hp->capacity = hp->size = 0;

void HeapDestroy(HP* hp)
{
	assert(hp);

	free(hp->a);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

堆入数据

因为堆存储结构就是一个数组，所以我们在数组末入数据，然后再进行向上调整算法。

void HeapPush(HP* ph, HPDataType x)
{
	assert(ph);
	// 判断扩容
	if (ph->size == ph->capacity)
	{
		// 扩容
		size_t newcapacity = ph->capacity == 0 ? 4 : 2 * ph->capacity;
		HPDataType* tmp = realloc(ph->a, newcapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			// 扩容失败
			printf("realloc fail\n");
			exit(-1);
		}

		ph->capacity = newcapacity;
		ph->a = tmp;
	}

	// 数组尾插数据
	ph->a[ph->size++] = x;

	// 向上调整
	// 参数： 堆数组，插入位置下标
	AdjustUp(ph->a, ph->size - 1);
}

向上调整算法

对插入数据大小不同，调整的最终条件也不同。

1. 插入最小值

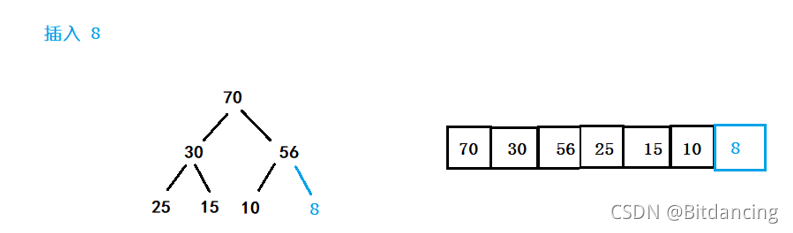
堆结构不发生变化

2. 插入比堆顶元素小

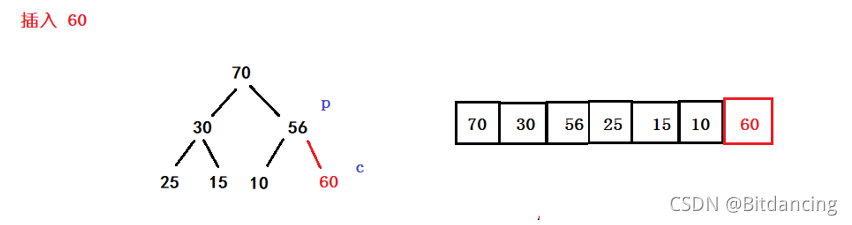
父亲比孩子小，交换元素。

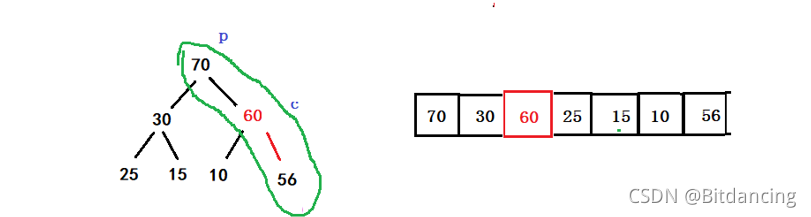
3. 插入元素比堆顶大

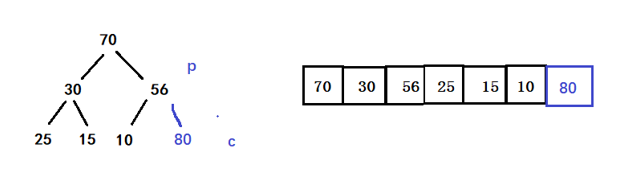
调整

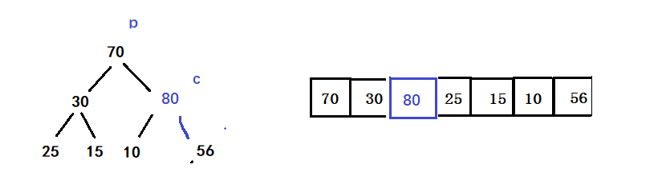
继续调整

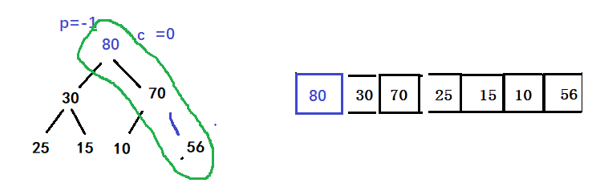
结束！

代码：

// 向上调整算法  此处以大堆为例
void AdjustUp(int* a, int child)
{
	assert(a);

	int parent = (child - 1) / 2;
	// 结束条件如果是parent>=0，会进入到下一个循环通过break跳出
	while (child > 0) 
	{
		if (a[parent] < a[child])
		{
			// 父亲结点值小于孩子结点
			Swap(&a[parent], &a[child]);

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

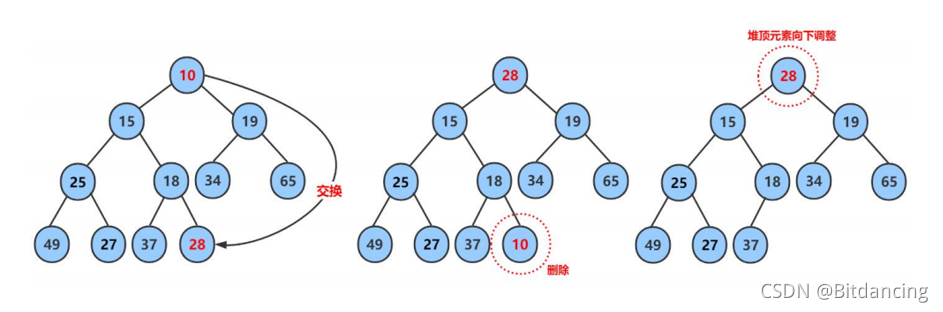
删除堆顶

堆顶pop分为三个主要步骤：首先堆顶和数组最后一个元素交换、数组个数减一、再进行向下调整算法。

void HeapPop(HP* hp)
{
	assert(hp);
	assert(hp->size != 0);

	// 交换数组首尾元素
	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	// 数组size减一
	hp->size--;
	// 堆顶元素向下调整
	AdjustDown(hp->a, hp->size, 0);
}

向下调整算法

调整结束的条件：

1. 到达叶子节点
2. 大堆：当大孩子小于等于父亲，退出
3. 小堆：小孩子 大于等于父亲，退出

以调整为小堆作为讲解

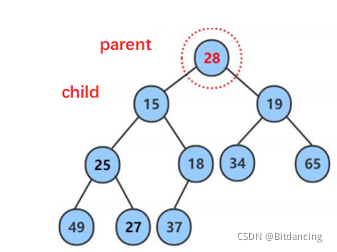
小孩子小于父亲，调整

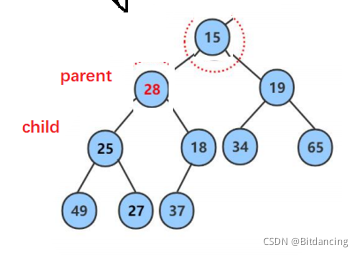
右孩子更小，小孩子小于父亲，调整

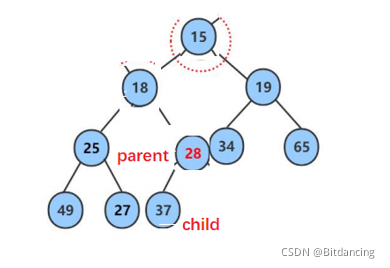
孩子大于父亲，结束调整。

// 向下调整算法，这里默认是调整成小堆
void AdjustDown(int* a, int n, int parent)
{
	assert(a);
	int child = parent * 2 + 1; // 默认是左孩子
	while (child < n)
	{
		// 找出小孩子
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;
		}

		// 如果小孩子比父亲小，则交换，继续调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

获得堆顶数据

进行空堆判断。

HPDataType HeapTop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));

	return hp->a[0];
}

判断空堆

bool HeapEmpty(HP* hp)
{
	assert(hp);

	return hp->size == 0;
}

堆大小

int HeapSize(HP* hp)
{
	assert(hp);

	return hp->size;
}

本文的重点在于堆向下和向上调整。

堆的应用 比如 TopK问题以及堆排序会在后面继续更新。

码文不易，欢迎三连，深鞠躬！