题目：

?

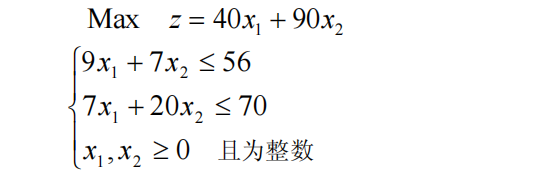求解思路：

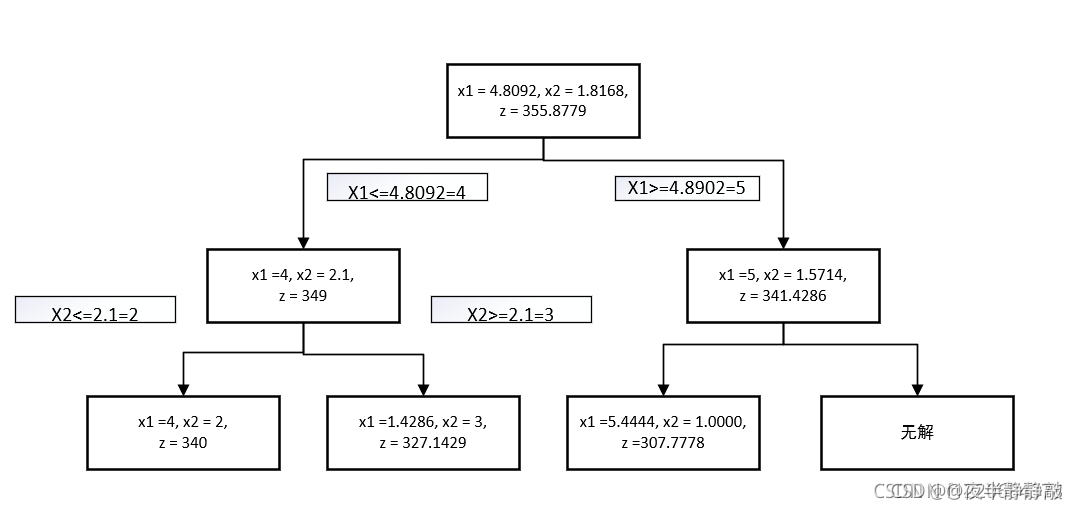
引用自：

https://blog.csdn.net/f1220684378/article/details/121197355

1.先用线性规划处理得到最优解

2.用分枝定界法，得到整数解。

3.进行剪枝，得到整数最优解

?求解过程：

在不考虑 $x_{1}$ ， $x_{2}$ 为整数的情况下，求解此线性规划

Matlab代码如下：

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=zeros(2,1);
[x,z]=linprog(-c,a,b,aeq,beq,lb);
x'
best = c*x

结果如下：

?因为 $x_{1}$ ， $x_{2}$ 首先对 $x_{1}$ 进行分枝，分别得到 $x_{1}\leq 4$ 或 $x_{1}\geq 5$ ?，首先对约束条件 $0\leq x_{1}\leq 4$ ， $x_{2}\geq 0$ 进行线性规划：

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[0;0];
ub = [4;inf]
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x

?然后对限制条件 $x_{1}\geq 5,x_{2}\geq 0$ 进行线性规划：

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[5;0];
ub = [inf;inf];
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x

?所以可以将z的取值范围进一步缩小为 $0\leqslant z\leqslant 349.$

?接下来在 $0\leq x_{1}\leq 4$ 基础上对 $x_{2}$ 进行分枝，分别得到 $0\leqslant x_{2}\leqslant 2$ 和 $x_{2}\geqslant 3$ ，首先对 $0\leq x_{1}\leq 4$ ， $0\leqslant x_{2}\leqslant 2$ 的限制条件上进行线性规划：

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[0;0];
ub = [4;2];
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x

? 再对 $0\leq x_{1}\leq 4$ ， $x_{2}\geqslant 3$ 的限制条件进行线性规划：
?

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[0;3];
ub = [4;inf];
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x

因此? $z$ 的取值区间缩短至 $\left [ 340,349 \right ]$ 。

接着在 $x_{1}\geq 5$ 基础上对 $x_{2}$ 进行分枝，分别为 $0\leqslant x_{2}\leqslant 1$ 和 $x_{2}\geqslant 2$ ，首先对? $x_{1}\geq 5$ ， $0\leqslant x_{2}\leqslant 1$ 的限制条件进行线性规划。

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[5;0];
ub = [inf;1];
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x

然后对? $x_{1}\geq 5$ ， $x_{2}\geqslant 2$ 的限制条件进行线性规划：
?

clear all;
clc;
c = [40,90];
a = [9 7;7 20];
b = [56;70];
aeq =[];
beq = [];
lb=[5;2];
ub = [inf;inf];
[x,z]=linprog(-c,a,b,aeq,beq,lb,ub);
x'
best = c*x