面试中不可少的几个二叉树相关试题
前序遍历和和中序遍历还原二叉树
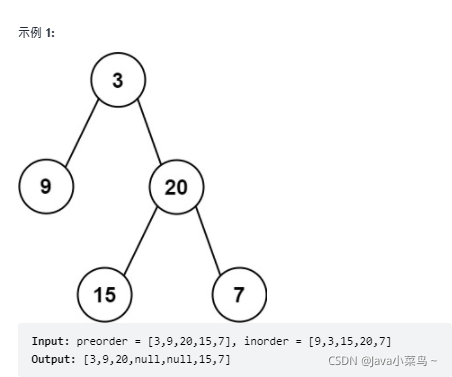
思路:
- 在前序遍历结果中确定二叉树的根结点(
原因:前序遍历是先遍历根结点,在遍历根的左子树,后遍历根的右子树); - 在中序遍历结果中找根的位置
pos,以pos为分界点,左边为根的左子树元素所处的位置,右边为根的右子树元素所处的位置; - 还原根结点;
- 递归还原根的左子树;
- 递归还原根的右子树
代码实现:
class Solution {
int index=0; //用来标记前序遍历中根的位置
TreeNode rebuilderTree(int[] preorder,int[] inorder,int left, int right){
if(index>=preorder.length || left >= right){
return null;
}
//从中序遍历结果中确定根的左右两颗子树位置元素
int pos=left;
while(pos<right){
if(inorder[pos]==preorder[index]){
//表明找到了根结点
break;
}
pos++;
}
// 从前序遍历结果中确定根,即index的位置 preorder[index]就是根的位置
//还原二叉树的根结点
TreeNode root=new TreeNode(preorder[index]);
index++;
//递归还原根的左子树
root.left=rebuilderTree(preorder,inorder,left,pos);
//递归还原根的右子树
root.right=rebuilderTree(preorder,inorder,pos+1,right);
return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
index=0;
return rebuilderTree(preorder, inorder,0,inorder.length);
}
}
中序遍历和和后序遍历还原二叉树
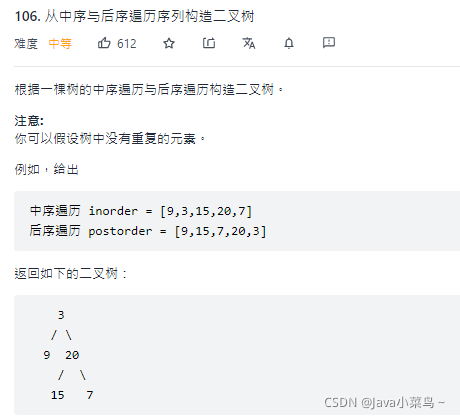
思路:
- 在后序遍历结果中确定二叉树的根结点(
原因:后序遍历是先遍历根的左子树,再遍历根的右子树,最后遍历根结点); - 在中序遍历结果中找根的位置
pos,以pos为分界点,左边为根的左子树元素所处的位置,右边为根的右子树元素所处的位置; - 还原根结点;
- 递归还原根的右子树;
- 递归还原根的左子树
代码实现:
class Solution {
int index=0; //用来标记前序遍历中根的位置
TreeNode rebuilderTree(int[] postorder,int[] inorder,int left, int right){
if(index<0 || left >= right){
return null;
}
//从中序遍历结果中确定根的左右两颗子树位置元素
int pos=left;
while(pos<right){
if(inorder[pos]==postorder[index]){
//表明找到了根结点
break;
}
pos++;
}
// 从前序遍历结果中确定根,即index的位置 postorder[index]就是根的位置
//还原二叉树的根结点
TreeNode root=new TreeNode(postorder[index]);
index--;
//递归还原根的右子树
root.right=rebuilderTree(postorder,inorder, pos+1,right);
//递归还原根的左子树
root.left=rebuilderTree(postorder,inorder,left ,pos);
return root;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
index=postorder.length-1;
return rebuilderTree(postorder, inorder,0,inorder.length);
}
}
二叉树构造字符串

思路:
该题目用到字符串,由于
string是不可变类型,要拼接所以使用stringbuilder;
注意:题目中的左括号是不能省略的,要不然分不清左右子树的位置;
代码实现:
class Solution {
public void preorder(TreeNode root, StringBuilder str) {
//树为空
if (root == null) {
return;
}
//转换根结点(就是打印)
str.append(root.val);
//递归转换根的左子树
//分下面两个情况
if (root.left != null) {
str.append('(');
preorder(root.left, str);
str.append(')');
}
if (root.left == null && root.right != null) {
str.append('(');
str.append(')');
}
//递归转换根的右子树
if (root.right != null) {
str.append('(');
preorder(root.right, str);
str.append(')');
}
}
public String tree2str(TreeNode root) {
StringBuilder str = new StringBuilder();
preorder(root, str);
return str.toString();
}
}
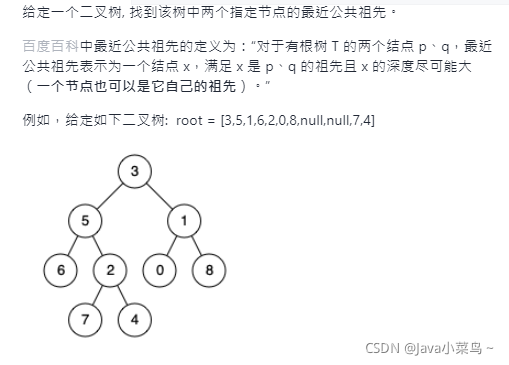
求二叉树的最近公共祖先
思路:
可以分三种情况来分析讨论:
情况一:该二叉树采用双亲表示法或者是采用孩子双亲表示法;
求公共祖先就变成了两个链表相交求交点的问题了;
情况二:
该二叉树如果为二叉搜索树,所谓二叉搜索树就是对于每个结点而言,都满足:(1)根结点大于根的左子树结点;(2)根结点小于根的右子树结点;
求公共祖先就有以下四种方式:
假设给定的两个结点,一个为x,一个为y;
(1)当x == root或y ==root时,最近的公共祖先一定为根结点;(原因:根结点是所有结点的祖先)
(2)当x .data< root.data && y.data>root.data时 ,或者当x .data> root.data && y.data<root.data,最近的公共祖先也是根结点(原因:x, y处在根结点的两侧);
(3)当x .data< root.data && y.data<root.data时,此时,x和y都处于根的左子树中,因此求最近的公共祖先就直接到根的左子树中找;
(4)当x .data> root.data && y.data>root.data时,此时,x和y都处于根的右子树中,因此求最近的公共祖先就直接到根的右子树中找;
情况三:该二叉树就是一棵普通的二叉树;
那么:
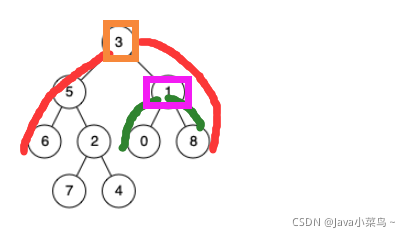
- 受情况一的启发,只要找到从根结点出发的到某个结点的路径中遇到那些结点,并将其保存;因为当路径中的结点找到之后,需要从下往上进行比较,因此借助栈来保存;
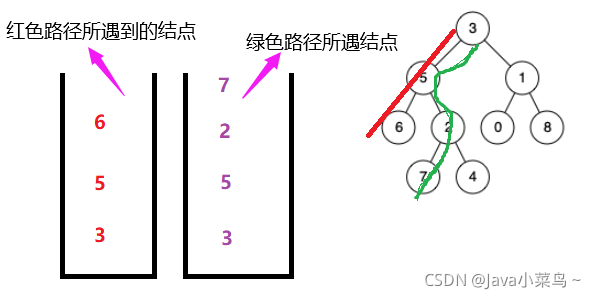
该种情况下
(1)当栈中所存元素不相等时,让元素多的出栈;
(2)相同且值域不同时,同时出栈;
(3)公共祖先就是栈中元素个数相同时且值域也相同的元素;
代码实现:
class Solution {
//获取根结点到某个结点对应路径中的所有遇到的结点
boolean getPathNode(TreeNode root,Stack<TreeNode> sPath,TreeNode node ){
if(node ==null || root==null){
//树为空或者结点为空
return false;
}
sPath.push(root);
if(root==node){
//表明是同一个结点
return true;
}
//左子树中找
if(getPathNode(root.left,sPath,node)){
return true;
}
//右子树中找
if(getPathNode(root.right,sPath,node)){
return true;
}
sPath.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//检测给定参数
if(root==null ||p==null ||q==null){
return null;
}
//找从root到p,q 对应路径中包含的所有结点
//保存到栈中
Stack<TreeNode> pPath=new Stack();
Stack<TreeNode> qPath=new Stack();
getPathNode(root,pPath,p);
getPathNode(root,qPath,q);
int pSize=pPath.size();
int qSize=qPath.size();
while(!pPath.empty() && !qPath.empty()){
if(pPath.peek()==qPath.peek()){
return pPath.peek();
}
if(pSize>qSize){
//让多的出栈
pPath.pop();
pSize--;
}else if(pSize<qSize){
qPath.pop();
qSize--;
}else{
//两个一样多时,同时出栈
pPath.pop();
qPath.pop();
pSize--;
qSize--;
}
}
return null;
}
}
- 同样的,受情况二启发:
- 如果知道一个结点在其子树中的位置,也能找到公共祖先;
代码如下:
class Solution {
boolean isNodeInTree(TreeNode root,TreeNode node){
//检测结点是否在树中
if(root==null || node ==null){
return false;
}
if(root==node){
return true;
}
if(isNodeInTree(root.left,node)){
return true;
}
return isNodeInTree(root.right,node);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//空树
if(root==null){
return null;
}
//树不为空
//p 和q 有一个在根的位置,公共祖先就是根
if(p == root|| q == root){
return root;
}
boolean ispInLeft=false;
boolean ispInRight=false;
boolean isqInLeft=false;
boolean isqInRight=false;
//检测p是否在root的左子树中
if(isNodeInTree(root.left,p)){
ispInLeft=true;
ispInRight=false;
}else{
ispInLeft=false;
ispInRight=true;
}
//检测q是否在root的左子树中
if(isNodeInTree(root.left,q)){
isqInLeft=true;
isqInRight=false;
}else{
isqInLeft=false;
isqInRight=true;
}
//检测p和q是否都在root的左子树中
if(ispInLeft && isqInLeft){
return lowestCommonAncestor(root.left,p,q);
}else if(ispInRight && isqInRight){
return lowestCommonAncestor(root.right,p,q);
}else{
return root;
}
}
}