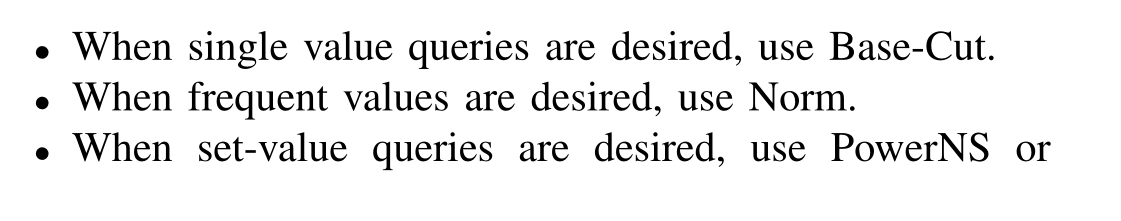Locally Differential Private Frequency Estimation with Consistency
目录
- Locally Differential Private Frequency Estimation with Consistency
- 1. INTRODUCTION
- 2. PROBLEM SETTING
- 3. FREQUENCY ORACLE PROYOCOLS
- 💜4. TOWARDS CONSISTENT FREQUENCY ORACLES
- 5. EVALUATION
- 6. RELATED WORK
- 7. CONCLUSION
论文链接.
论文主要内容
已知:在频率估计(Frequency Oracle - FO)中所有值的频率均为非负,并且所有频率总和为1
利用已知知识,在FO协议中添加一个后处理步骤 Post-Processing ,可以显著提高(包括单个值的频率、频繁项的频率以及子集的频率)等各类任务的准确率
1. INTRODUCTION
国内外研究现状:
-
现有的FO协议被设计为:最小化方差的同时,提供对单个值的无偏估计。但,它们在某些任务中表现不佳
-
现有的FO协议并没有很好的利用任何关于要估计的分布的先验知识
先验知识:1)所有值的频率均为非负,2)所有频率总和为1
利用先验知识引入bias偏差
在利用这些先验知识的时候,会给最终的估计结果引入bias 偏差
- 例:施加非负约束,则导致了最终估计引入了positive bias的副作用,这些bias会导致一些的查询结更不准确
- 提高了对单个值频率估计的准确性
- 但是,范围查询(子集)中引入的positive bias越来越多,子集的频率的准确性可能会降低
实验
- 实验设置
- 10种方法:不同的利用先验知识方法
- 3个任务
- 单个值的频率 query the frequency of every value in the domain
- 频繁项的频率 query the frequencies of the most frequent values
- 子集的频率 query the aggregate frequencies of subsets of values
- 实验结果:没有一种方法在所有任务中都优于其他方法
- 只使用先验知识1),对单个值的频率估计任务表现最好
- 只使用先验知识2),对频繁项频率估计的任务表现最好
- 结合使用先验知识1和先验知识2,对子集的频率估计任务表现最好
2. PROBLEM SETTING
略
3. FREQUENCY ORACLE PROYOCOLS
使用pure protocol来表示FO协议
f
~
(
v
)
=
I
v
/
n
?
q
?
p
?
?
q
?
\widetilde{f}(v)=\frac{I_v/n-q^*}{p^*-q^*}
f
?(v)=p??q?Iv?/n?q??
f
~
是
\widetilde{f}是
f
?是 无偏估计,其方差为
σ
v
2
=
q
?
(
1
?
q
?
)
n
(
p
?
?
q
?
)
2
+
f
v
(
1
?
p
?
?
q
?
)
n
(
p
?
?
q
?
)
\sigma_v^2=\frac{ q^*(1-q^*)}{n(p^*-q^*)^2}+\frac{f_v(1-p^*-q^*)}{n(p^*-q^*)}
σv2?=n(p??q?)2q?(1?q?)?+n(p??q?)fv?(1?p??q?)?
方差推理过程见下图:
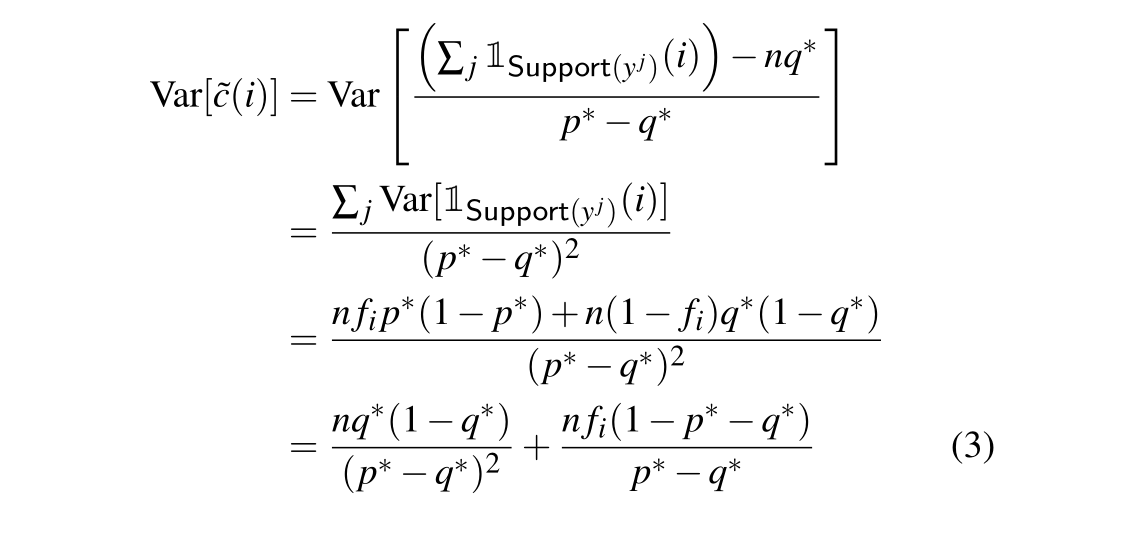
3.1 Generalized Random Response ——GRR
f ~ ( v ) = I v / n ? q ? p ? ? q ? = I v / n ? 1 e ε + d ? 1 e ε ? 1 e ε + d ? 1 \widetilde{f}(v)=\frac{I_v/n-q^*}{p^*-q^*}=\frac{I_v/n-\frac{1}{e^{\varepsilon}+d-1}}{\frac{e^{\varepsilon}-1}{e^{\varepsilon}+d-1}} f ?(v)=p??q?Iv?/n?q??=eε+d?1eε?1?Iv?/n?eε+d?11??
3.2 Optimized Local Hashing OLH
在OLH中,在Encoding和Perturbe步骤中都会有信息损失,而参数d的选择则是这两个步骤的信息损失之间的权衡,当g=eε+1(或最接近的整数),方差
f ~ ( v ) = I v / n ? q ? p ? ? q ? = I v / n ? 1 g p ? ? 1 g \widetilde{f}(v)=\frac{I_v/n-q^*}{p^*-q^*}=\frac{I_v/n-\frac{1}{g}}{p^*-\frac{1}{g}} f ?(v)=p??q?Iv?/n?q??=p??g1?Iv?/n?g1??
3.3 Accuracy
参考论文
论文链接.
由于cv服从Binomial分布,通过中心极限定理得: f ~ v ≈ f v + N ( 0 , σ v ) \widetilde{f}_v \approx f_v+\mathcal{N}(0,\sigma_v) f ?v?≈fv?+N(0,σv?)
当d较大,而ε不是特别大得时候,可以通过忽略fv得到下式:
σ
2
≈
q
?
(
1
?
q
?
)
n
(
p
?
?
q
?
)
2
f
~
v
≈
f
v
+
N
(
0
,
σ
)
\sigma^2 \approx \frac{q^*(1-q^*)}{n(p^*-q^*)^2} \\ \widetilde{f}_v \approx f_v + \mathcal{N}(0,\sigma)
σ2≈n(p??q?)2q?(1?q?)?f
?v?≈fv?+N(0,σ)
💜4. TOWARDS CONSISTENT FREQUENCY ORACLES
Base
不做 post-processing,没有偏差,方差可以通过理论计算
4.1 Baseline Methods
4.1.1 Base-Pos
在执行FO协议后,将所有负频率估计都转化为0
-
减少了方差:通过把错误的负值转化为0,更加接近真实值
-
Base-Pos引入了 positive bias 正偏差:一些负偏差通过这个过程消除,而正偏差没有被去除
Lemma1
所有的值v 经过Base-Pos都引入了正偏差
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EuDle974-1636380936690)(C:/Users/CLOUDNESS/AppData/Roaming/Typora/typora-user-images/image-20211102195537086.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8UiZhqIT-1636380936691)(C:/Users/CLOUDNESS/AppData/Roaming/Typora/typora-user-images/image-20211102195545352.png)]
p o s i t i v e ? b i a s = E [ f v ’ ] ? f v > 0 positive\ bias =E[f^{’}_v]-f_v>0 positive?bias=E[fv’?]?fv?>0
4.1.2 Post-Pos
对于每个查询(query:这里可以是单个值的频率、频繁项的频率以及子集的频率)结果,如果是负值,则转化为0
-
**v.s. Base-Pos :**不对估计的分布进行后处理,而是分别对每个查询结果进行后处理
当query为查询单个值的频率的时候 等价 Base-Pos
-
当query为查询子集的频率,
- 由于结果通常大于0,所以与Base相似
- 引入的偏差要比Base-Pos来的小
- 可能会给出不一致inconsistency的结果,A∪B的频率 ≠ A + B的频率
4.1.3 Base-Cut
在执行FO协议后,将所有小于敏感度阈值的频率估计都转化为0
- 最初设计目标:恢复频繁项的频率值,所以只有高于阈值的估计才会被考虑
阈值公式
T = F ? 1 ( 1 ? α d ) σ T=F^{-1}(1-\frac{\alpha}{d})\sigma T=F?1(1?dα?)σ
d:域大小
F-1(x):是标准正态分布的累计函数的反函数
σ:LDP机制的标准差
α:控制低频但频率估计高于阈值的项的数量,
α参数的选择是在false positive和false negatives 之间进行的权衡
对于一个真实频率为0的值,其经过FO协议后的频率估计大于T的概率至多为 α/d

已知一个频率估计大于T,则这个值的真实频率为0的概率至多为 d × α / d = α d \times \alpha/d = \alpha d×α/d=α
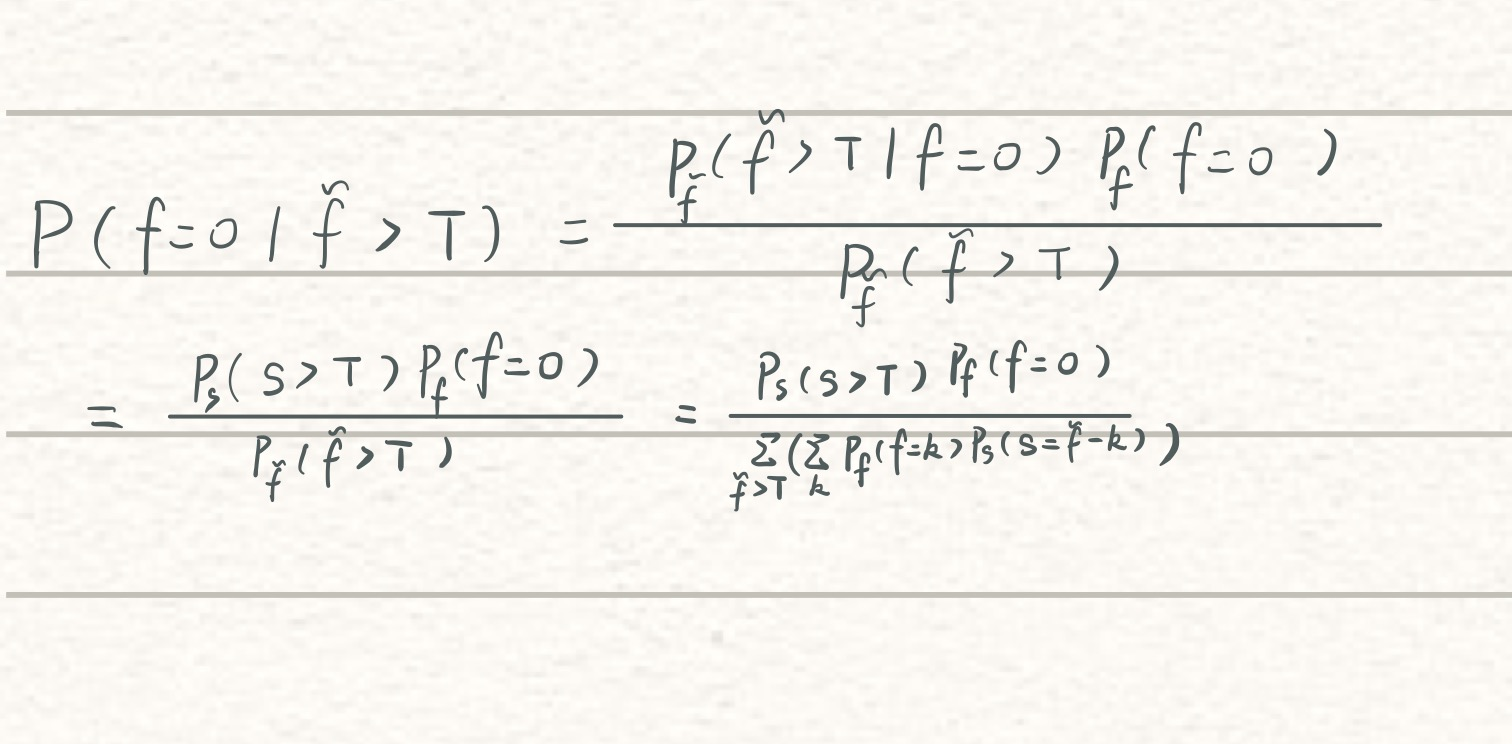
- α越大,1-α/d越小,即密度概率曲线下面积越小,则T越小
- α参数的选择是在false positive和false negatives 之间进行的权衡
- 常规统计学中设置,α=5%,在实验中表现不好,是因为当d和ε不是特别大时,这个阈值T太大了
- 本文中设置α=2,如果由20个项的频率估计>T,则true positive : false positive = 10: 1
方法评价
- 确保频率估计无负值,不确保频率估计总和为1
- 经过Base-Cut的频率估计,要么较高(大于T),要么为0
- 对于每个非零的频率估计值,都会收到两种方向偏差的作用力
- negative bias effect: 当估计值被削减到0
- positive bias effect: 当较大的噪声导致估计值高于阈值,所得的估计值高于真实频率
4.2 Normalization Method
通过归一化方法,确保整个域的频率估计和为1
Lemma 2
通过归一化方法调整无偏估计,使得频率估计的和为1,那么整个域引入的偏差和也为0
4.2.1 Norm
在执行FO协议后,给每个频率估计加上δ,以实现总和为1
-
该方法不强制要求非负性
-
对于GRR、Hadamard Response 和Subset Selection这个方法没有意义,因为这些协议的估计总和已经为1
-
对于OLH,协议总和不再为1
For OLH, however, each user reports a randomly selected subset whose size is a random variable, and Norm would change the estimations.
Lemma 3
Norm 为每一个值提供无偏估计
-
已知 根据Norm 的定义有: ∑ v ∈ D f v ‘ = ∑ v ∈ D f ~ v + δ \sum_{v\in D}f^‘_v=\sum_{v \in D}\widetilde{f}_v+\delta ∑v∈D?fv‘?=∑v∈D?f ?v?+δ 根据FO协议的输出是无偏估计有: E ( f ~ v ) = f V E(\widetilde{f}_v)=f_V E(f ?v?)=fV?
-
易混淆 FO协议无偏只代表其分布的均值为fv,不代表一次实例就是fv; 同理,FO协议无偏,表示其估计的和的均值为1,但本身可能不为1
-
证明

Lemma 4
通过归一化方法调整无偏估计,使得频率估计的和为1的同时所有值非负,那么会对接近0的值引入正偏差
证明:对于一些足够接近0的值,其存在估计为正的可能性,也存在估计为负的可能性,但经过归一化方法后,只能为正,所以引入了一个 positive bias
引理4说明:任何同时满足下图两个约束的方法引入的偏差都不能全为0

4.2.2 Norm-Mul
在执行FO协议后,将所有负频率估计都转化为0,再给每个频率估计乘以一个乘数因子γ,以实现总和为1
∑
v
∈
D
m
a
x
(
γ
×
f
~
v
,
0
)
=
1
\sum_{v\in D}max(\gamma \times \widetilde{f}_v,0)=1
v∈D∑?max(γ×f
?v?,0)=1
f v ‘ = m a x ( γ × f ~ v , 0 ) f^‘_v=max(\gamma \times \widetilde{f}_v,0) fv‘?=max(γ×f ?v?,0)
- 该方法在比较 平滑 的数据上表现更好,对于分布不对称的方法(往往是LDP感兴趣的),表现得很差
- 该方法针对低频项引入 positive bias, 针对高频项引入 negative positive, 且一个值的真实频率越高,引入的 negative bias 越大
- 原因:γ的值通常在[0,1]范围内,则频率越高,削减的值越多
4.2.3 Norm-Sub
在执行FO协议后,给所有频率加上δ,再将所有负值都转化为0,以实现总和为1
∑
v
∈
D
m
a
x
(
δ
+
f
~
v
,
0
)
=
1
\sum_{v\in D}max(\delta + \widetilde{f}_v,0)=1
v∈D∑?max(δ+f
?v?,0)=1
f v ‘ = m a x ( δ + f ~ v , 0 ) f^‘_v=max(\delta + \widetilde{f}_v,0) fv‘?=max(δ+f ?v?,0)
- 该方法针对低频项引入 positive bias, 针对高频项引入 negative bias
- 但是相较 Norm-Mul 其bias 的分布要更加均匀
4.2.4 Norm-Cut
在执行FO协议后,将所有的负值和较小的正值都转化为0,以实现总和为1
-
在Norm-Sub中,高频项有较高的negative bias,=》解决思路:讲较低的正值转化为0
-
Norm-Cut后处理的两种情况
-
∑ v ∈ D m a x ( f ~ v , 0 ) ≤ 1 \sum_{v \in D}max(\widetilde{f}_v,0)\le1 ∑v∈D?max(f ?v?,0)≤1, 简单将每个负值转化为0
-
∑ v ∈ D m a x ( f ~ v , 0 ) > 1 \sum_{v \in D}max(\widetilde{f}_v,0) > 1 ∑v∈D?max(f ?v?,0)>1,找到一个值 θ \theta θ使得大于 θ \theta θ的值的和小于等于1,即 ∑ v ∈ D ∣ f ~ v > θ f ~ v ≤ 1 \sum_{v \in D|\widetilde{f}_v>\theta}\widetilde{f}_v\le1 ∑v∈D∣f ?v?>θ?f ?v?≤1
f ‘ = 0 , ?? f ~ v < θ f ‘ = f ~ v , ?? f ~ v ≥ θ f^‘=0,\ \ \widetilde{f}_v<\theta\\ f^‘=\widetilde{f}_v,\ \ \widetilde{f}_v \ge \theta f‘=0,??f ?v?<θf‘=f ?v?,??f ?v?≥θ
-
-
v.s. Base-Cut
阈值的选择方法不同,Norm-Cut可能产生 频率估计的和小于1的结果
4.3 Constrained Least Squares
**CLS:**在执行FO协议后,使用带有约束条件的最小二乘法来恢复估计值
KaTeX parse error: Expected 'EOF', got '&' at position 12: minimize: &?||f^‘-\widetild…
通过KKT求得最优解过程如下

f
v
‘
=
f
~
v
?
1
D
1
(
∑
v
∈
D
1
f
~
v
?
1
)
f^‘_v=\widetilde{f}_v-\frac{1}{D_1}(\sum_{v\in D_1}\widetilde{f}_v-1)
fv‘?=f
?v??D1?1?(v∈D1?∑?f
?v??1)
Norm-Sub 就是 CLS公式的解
δ = ? 1 D 1 ( ∑ v ∈ D 1 f ~ v ? 1 ) \delta = -\frac{1}{D_1}(\sum_{v\in D_1}\widetilde{f}_v-1) δ=?D1?1?(v∈D1?∑?f ?v??1)
4.4 Maximum Likelihood Estimation
将问题视为恢复真实的概率值
4.4.1 MLE-Apx
在执行FO协议后,计算带有约束条件的MLE(最大似然函数)来恢复估计值
最大似然函数公式推导
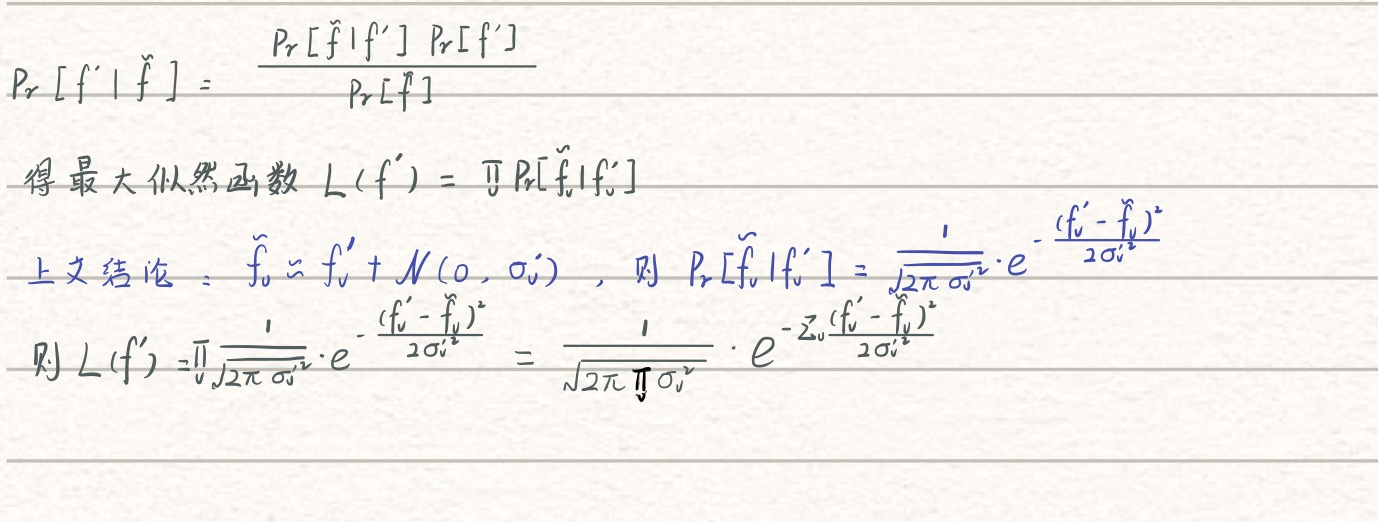
同理使用KKT求解最优值
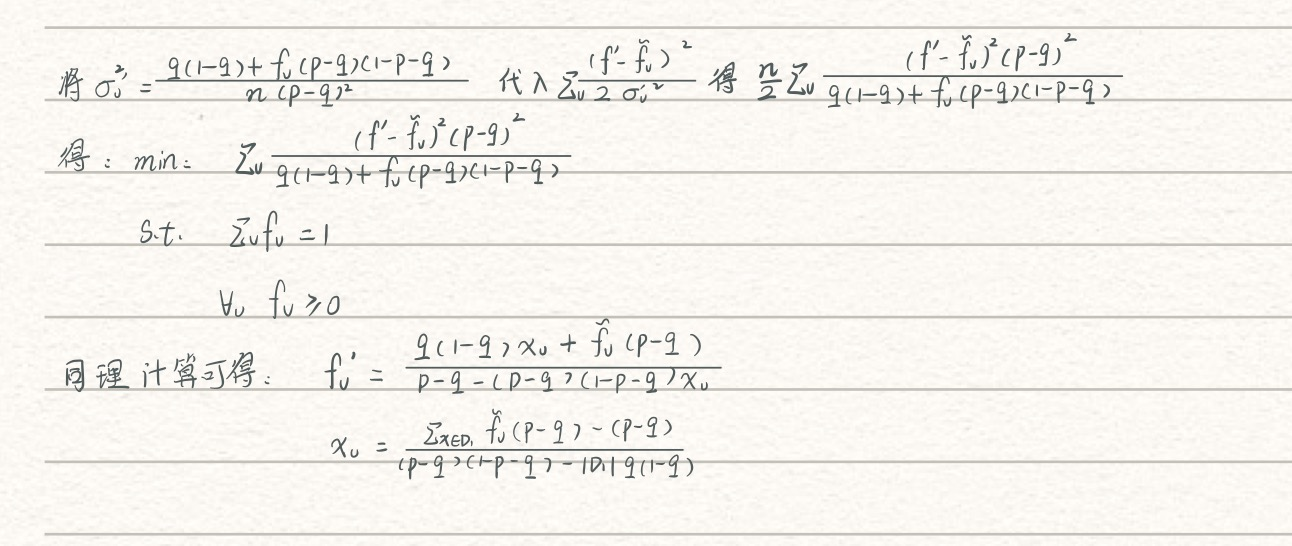
可将公式改写为
KaTeX parse error: Expected 'EOF', got '&' at position 9: f^‘_v =&? \widetilde{f}_…
-
因此MLE-Apx 很像Norm-Sub 和 Norm-Mul的结合
-
当 y ~ 1 y \sim 1 y~1时,MLE-Apx与Norm-Sub很接近
4.5 Least Expected Square Error
首先假设数据遵循某种类型的分布(但参数未知),然后通过最小期望平方误差来拟合分布的参数、
4.5.1 Power
参考论文
论文链接.
假设真实频率服从Power-Law分布,然后最小化期望的平方误差.
此方法需要已知数据的概率分布,或数据的知识来获得对应的概率分布
-
认为频率估计由两部分组成 f ~ v ≈ f v + N ( 0 , σ ) \widetilde{f}_v \approx f_v + \mathcal{N}(0,\sigma) f ?v?≈fv?+N(0,σ)
-
最小化 E [ ( f v ? f v ‘ ) 2 ∣ f ~ v ] E[(f_v-f_v^‘)^2|\widetilde{f}_v] E[(fv??fv‘?)2∣f ?v?],
最优化结果得到频率估计计算公式如下
f ‘ = ∑ k k ? P r ( f = k ∣ f ~ = f ~ v ) f^‘=\sum_k k·Pr(f=k|\widetilde{f}=\widetilde{f}_v) f‘=k∑?k?Pr(f=k∣f ?=f ?v?) -
得到校正频率估计 f v ‘ f_v^‘ fv‘?公式如下
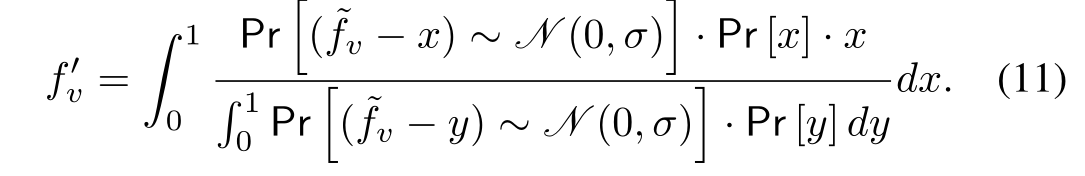

- 如果噪声太多,或拟合的分布与真实分布不同,则使得校正结果的精度较差
4.5.2 PowerNS
由于Power方法独立对每个 f v ‘ f_v^‘ fv‘?进行校正,所以其无法满足约束2)sum=1,故我们对Power的结果使用Norm-Sub后处理方法
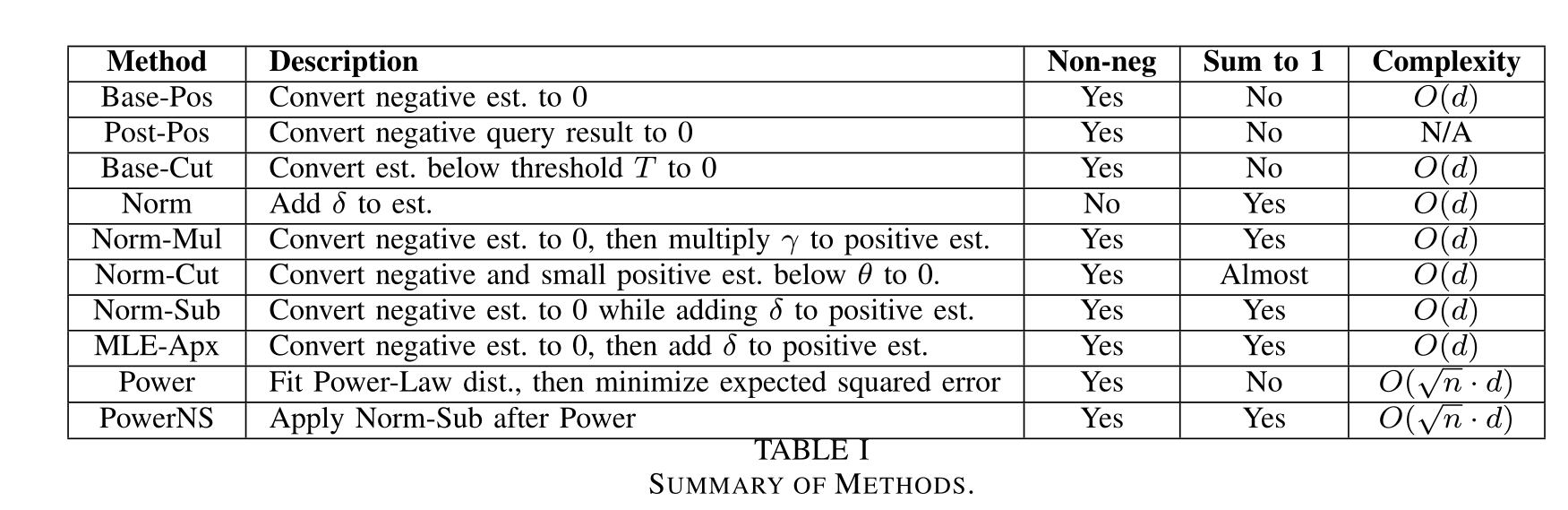
4.6 Summary
5. EVALUATION
对于全域查询full-domain query,Base-Cut表现最佳
对于子集查询set-value query,PowerNS表现最佳
对于频繁项查询high-frequency-value query,Norm表现最佳
5.1 Experimental Setup
数据集
两个数据集
-
一个合成数据集,服从Zipf幂律分布
-
一个Emoji数据集

度量方法
使用MSE方法度量
-
对于全域查询
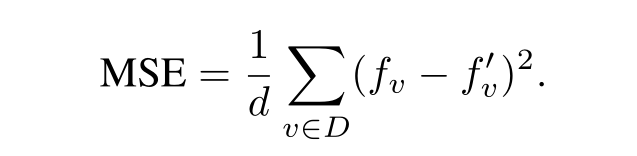
-
对于频繁项查询
我们计算top-k频率的项,而不是整个域D
-
对于子集查询
不同于度量单个项的误差,我们首先度量子集的误差。即,先对一组值的频率求和,再度量误差
5.2 Bias-variance Evaluation
Figure 1
针对Zipf数据集吗,蓝线为真实概率分布,绿线为不同的后处理后的概率估计
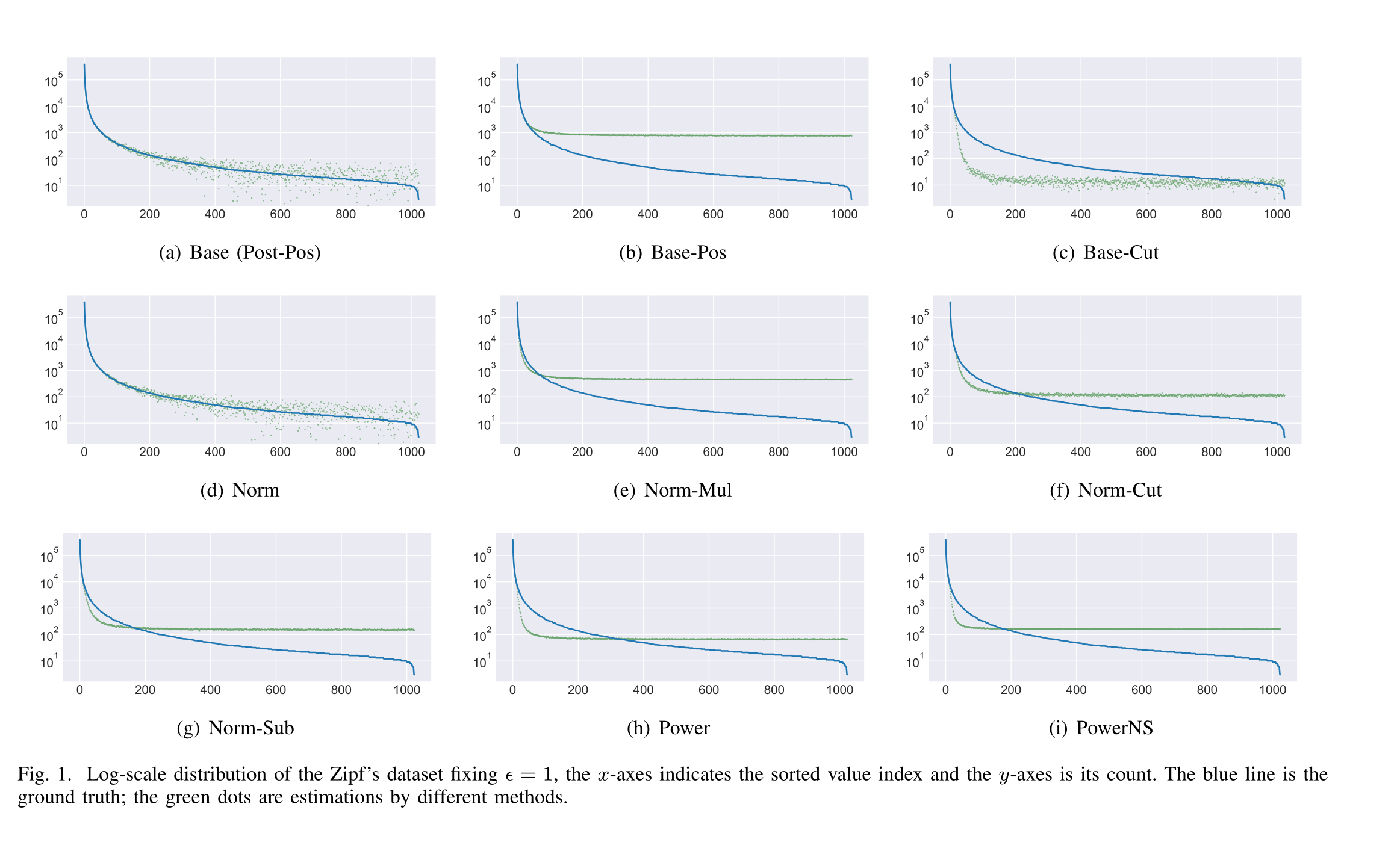
Figure 2
- 经验偏差,可以得到Base、Norm无偏
- Base-Pos有 positive bias
- Base-Cut对于频繁项无偏,对于部分的值,收到positive bias和 negative bias ,所以可能会出现无偏估计
- 对于Norm-Cut分析同样适用,Norm-Sub的阈值要比Base-Cut来的小
- 对于Norm-Sub,对 所有的值减去δ,然后将所有小于零的值,置为0
- 对于Power对频繁项没有太大变化,和Norm-Cut类似,对于低频的值,有很大的偏差
- 对于PowerNS于Power相近,在Power后执行Norm-Sub,减去一些估算值
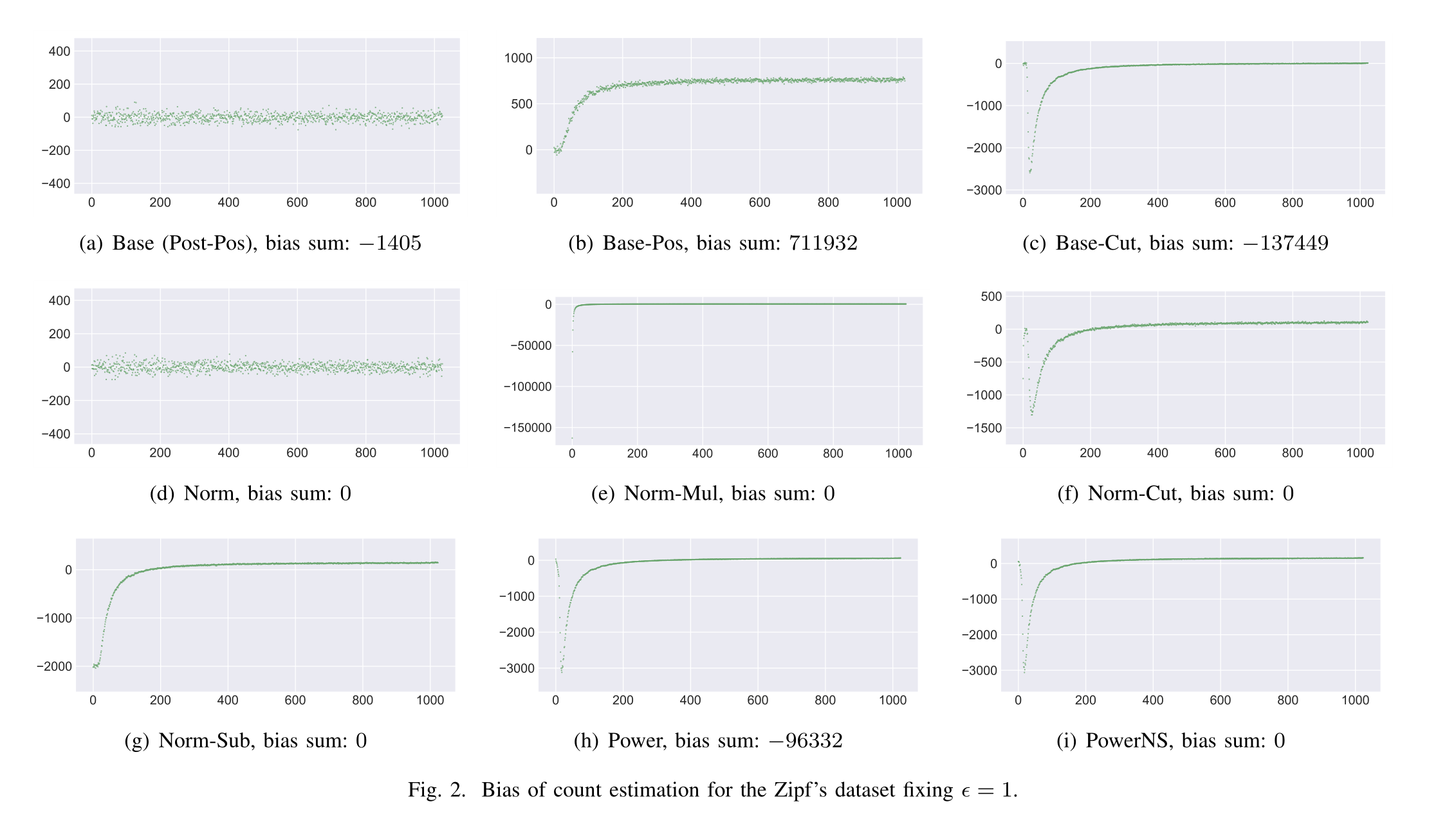
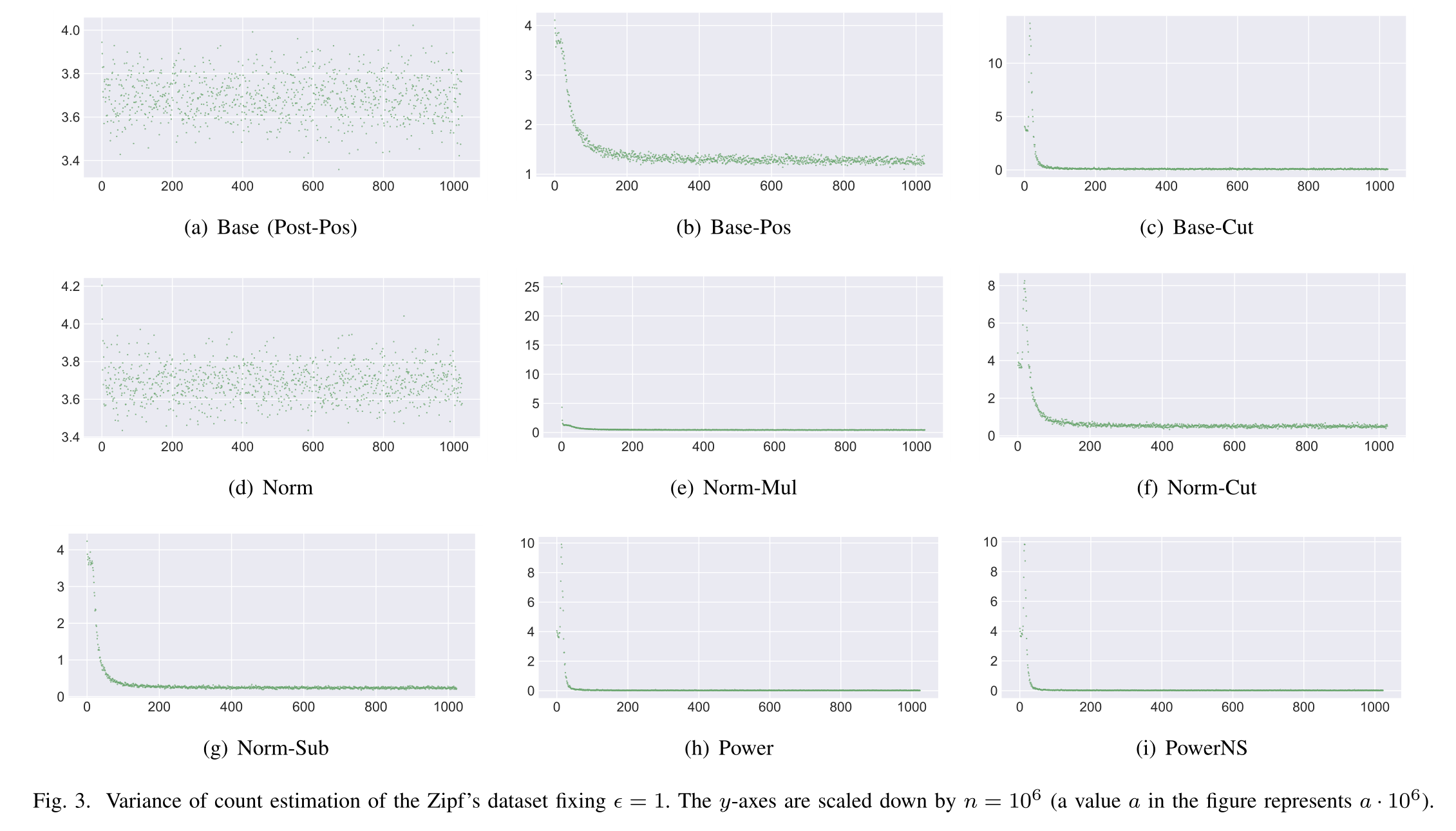
Figure 3
方差
- Base和Norm中所有值的方差都是相似的,Norm中稍好一些
- 其他的方法,方差随着频率估计排名的下降而下降,因为对于低频项,他们的估计和均值多为0
5.3 Full domain Evaluation
具体见论文
5.4 Set-value Evaluation
具体见论文
5.5 Frequent-value Evaluation
具体见论文
5.6 Discussion
-
Norm-Sub和MLE-Apx表现相近;Base和Norm表现相近
-
如果要进行 set-value estimation 可以选择PowerNS,如果set固定,可以对经过Norm-Sub处理的数据集选择最优方法
直觉是,PowerNS 改进了MLE(即Norm-Sub,一种理论证明方法)因为它使得数据更加接近真实频率估计的分布
-
如果要进行frequent-value estimation 可以选择Norm,虽然也可以选择Base但是Norm减少了方差,这两个方法不会显著的改变任何值
-
如果要进行single value estimate 可以选择Base-Cut
后处理准则