前言:本文使用的损失函数为KL离散构建的损失函数,无公式推导部分;代码部分为自定义函数,非sklearn。
逻辑回归KL离散构建的损失函数为:?
?
其中m表示样本数量;p_1表示标签为1的概率;y^{(i)}表示第i条样本的真实值;x^{(i)}表示第i条样本数据(包含多个特征,即一行数据;最后一个值为1)。?
损失函数求导(梯度表达式)为:?
?
公式推导思路:
- BCE可以拆解为对
和
分别对w、b求导;
- 将上述结果带入
、
逻辑回归自定义函数:
def logit_gd(X,w,y):
"""
返回逻辑回归梯度下降的结果
"""
m=X.shape[0]
return (X.T.dot(sigmoid(X.dot(w))-y))/m如何使用自定义逻辑回归函数做预测模型?(案例:标签分类)
思路:
????????1. 创建自定义数据集
? ? ? ? 2. 用逻辑回归预测标签,画出学习曲线进行模型评估
1. 创建自定义数据集,此处使用自定义函数创建自定义数据集?。
def arrayGenCla(num_examples=1000,num_inputs=2,num_class=3,deg_dispersion=[4,2],bias=False):
mean_=deg_dispersion[0] # 设定数据均值
std_=deg_dispersion[1] # 设定数据方差
k=mean_*(num_class-1)/2 # 设定惩罚因子,将数据调整为围绕原点分布
cluster_l=np.empty([num_examples,1])
lf=[]
ll=[]
for i in range(num_class): # 创建各个分类的数据
data_temp=np.random.normal(i*mean_-k,std_,size=(num_examples,num_inputs))
lf.append(data_temp)
labels_temp=np.full_like(cluster_l,i)
ll.append(labels_temp)
features=np.concatenate(lf) # 把分类的数据合并
labels=np.concatenate(ll)
if bias== True: # 如果设定的数据集为多元,则features最后一列加“1”
features=np.concatenate((features,np.ones(labels.shape)),1)
return features,labels?2. 用逻辑回归预测标签,画出学习曲线进行模型评估
首先,使用自定义函数创建一个数据集。该数据集有两个标签,重叠部分较少。?
np.random.seed(9)
f,l=arrayGenCla(num_class=2,deg_dispersion=[6,2],bias=True)
plt.scatter(f[:,0],f[:,1],c=l)
plt.show()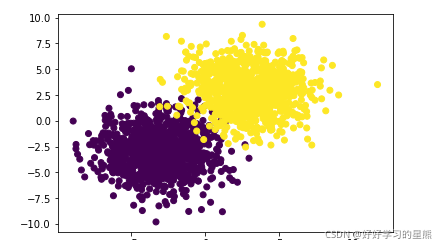
然后,切分数据集为训练集和测试集。使用梯度下降求解参数w,保存每次w迭代后的结果,求出在训练集和测试集的模型表现,画出学习曲线。
代码中部分为自定义函数,补充在学习曲线后面。
X_train,X_test,y_train,y_test=array_split(f,l,random_state=9)
X_train[:,:-1]=z_score(X_train[:,:-1])
X_test[:,:-1]=z_score(X_test[:,:-1])
np.random.seed(24)
w=np.random.randn(f.shape[1],1)
score_train=[]
score_test=[]
for i in range(num_epoch):
w=sgd_cal(X_train,w,y_train
,logit_gd
,batch_size=batch_size
,epoch=1
,lr=lr_init*lr_lambda(i))
score_train.append(logit_acc(X_train,w,y_train,thr=0.5))
score_test.append((logit_acc(X_test,w,y_test,thr=0.5)))
plt.plot(range(num_epoch),score_train,label='score_train')
plt.plot(range(num_epoch),score_test,label='score_test')
plt.legend()
plt.show()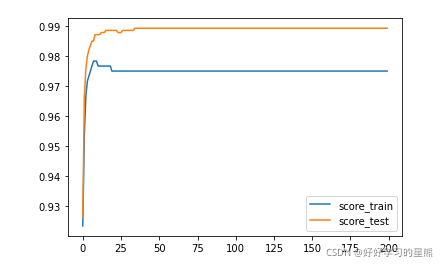
def logit_cla(yhat, thr=0.5):
"""
返回逻辑回归类别输出函数
"""
ycla = np.zeros_like(yhat)
ycla[yhat >= thr] = 1
return ycla
def logit_acc(X,w,y,thr=0.5):
"""
返回逻辑回归的评估指标
"""
y_hat=sigmoid(X.dot(w))
y_cal=logit_cla(y_hat,thr=thr)
return(y_cal==y).mean()结论:由学习曲线可知,迭代大概25次后,参数w已经接近最优解,模型趋于稳定。模型设定考虑的因素比较简单,w在测试集上表现更好为偶然。
如果数据重叠较多,那么这个逻辑回归模型的表现会怎么样呢?下面再次进行实验:
# 重合程度较大的数据集上逻辑回归的表现结果
np.random.seed(9)
f_1,l_1=arrayGenCla(num_class=2,deg_dispersion=[6,4],bias=True)
plt.scatter(f_1[:,0],f_1[:,1],c=l)
plt.show()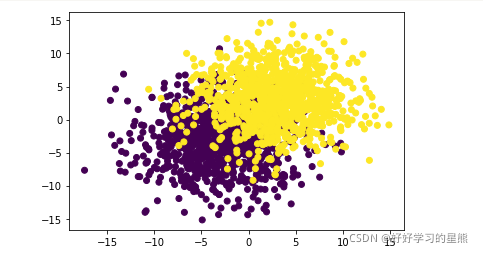
X_train,X_test,y_train,y_test=array_split(f_1,l_1,random_state=9)
X_train[:,:-1]=z_score(X_train[:,:-1])
X_test[:,:-1]=z_score(X_test[:,:-1])
np.random.seed(24)
w=np.random.randn(f.shape[1],1)
score_train=[]
score_test=[]
for i in range(num_epoch):
w=sgd_cal(X_train,w,y_train
,logit_gd
,batch_size=batch_size
,epoch=1
,lr=lr_init*lr_lambda(i)
)
score_train.append(logit_acc(X_train,w,y_train,thr=0.5))
score_test.append((logit_acc(X_test,w,y_test,thr=0.5)))
plt.plot(range(num_epoch),score_train,label='score_train')
plt.plot(range(num_epoch),score_test,label='score_test')
plt.legend()
plt.show()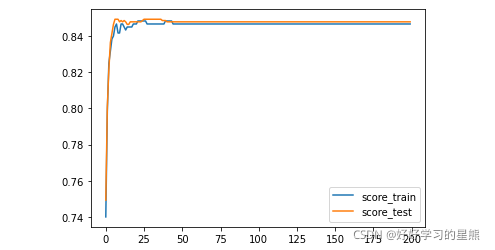
结论:由学习曲线可知,同样在迭代25次后,模型趋于平稳,准确率下降到了0.85左右。?