栈的概念
栈是一种特殊的线性表,只允许在固定的一段进行插入删除操作。
进行数据插入删除的一端叫做栈顶,另一端叫做栈底。
栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
栈的实现分析
先考虑需要实现的功能(考虑结构设计时是从需要实现的功能出发的):
- 初始化
- 入栈
- 出栈
- 获取栈顶元素
- 获取栈中有效元素的个数
- 判空。栈为空返回true;不为空返回false
- 销毁
再考虑栈的结构定义
可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
这里实现动态数组栈。
这里由于是动态增长的栈,在栈这个结构中应当有一个动态数组,另外还需要一个变量表示数组中有效元素数量,以及数组实际大小(容量)以便确定是否需要扩容。这一点和顺序表很类似。
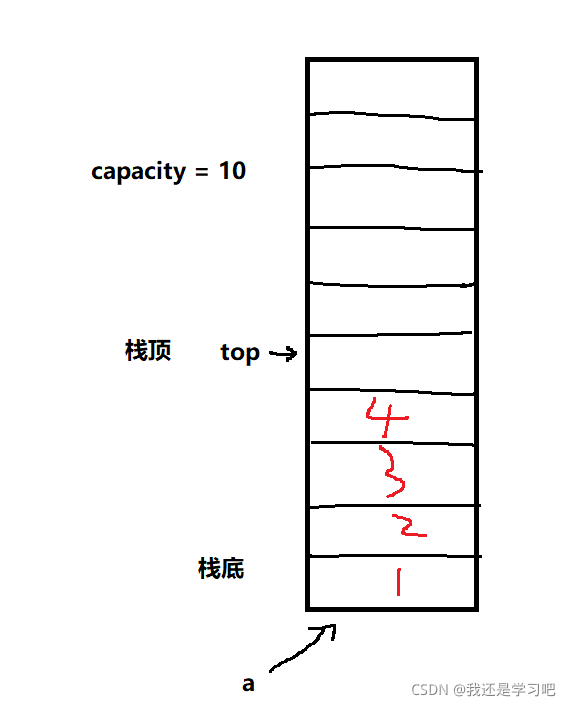
结构定义
//先定义数据类型
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
初始化栈
在这里我们实现的栈是由使用方定义并传其地址给函数初始化,
而不是由函数创建栈并返回指向这个栈的指针。
top标记的是下一个数据放入位置的下标。
void StackInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
销毁栈
数组栈是一段连续的空间,由realloc实现,释放一次就够了。
void StackDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
入栈
入栈前需要判断栈是否满了,满了就扩容。这里和顺序表的处理方法是一样的。
void StackPush(ST* ps, STDataType x)
{
assert(ps);
if(ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity*2;
SDTataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType)*newcapacity);
if(tmp == NULL)
{
printf("realloc fail");
exit(-1);
}
}
ps->a[ps->top] = x;
ps->top++;
}
出栈
尽量使用提供的接口判空,一方面避免代码重复,发生错误时只需要修改实现这个功能的函数,另一方面可能在某些时候我们并不知道内部结构。
void StackPop(ST* ps)
{
assert(ps);
assert(!StackEmpty(ps));
ps->top--;
}
取出栈顶元素
STDataType StackTop(ST* ps)
{
assert(ps);
assert(!StackEmpty(ps));
return ps->a[ps->top-1];
}
计算栈中有效数据个数
int StackSize(ST* ps)
{
assert(ps);
return ps->top;//注意下标从0开始
}
判空
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
队列的概念
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 的特点
队头:进行删除操作的一端称为队头
队尾:进行插入操作的一端称为队尾
队列实现分析
先分析需要实现哪些功能:
- 初始化
- 入队
- 出队
- 获取队头元素
- 获取队尾元素
- 获取队列中有效元素个数
- 判空
- 销毁
再分析采用什么结构
可以用数组实现也可以用链表实现,但是数组不方便头删,所以用链表更好。
这里用的是不带头的单向链表。
最后分析队列结构应该是怎样的:
既然是用链表实现,则要先实现链表,把这个链表当作队列,为了方便尾插,我们用一个头指针head指向队头,一个尾指tail针指向队尾。把这两个指针封装起来就是我们的队列了。(当然也可以再加一个变量size表示队列中有效元素个数,这样可以使得QueueSize时间复杂度为O(1),这里不加)
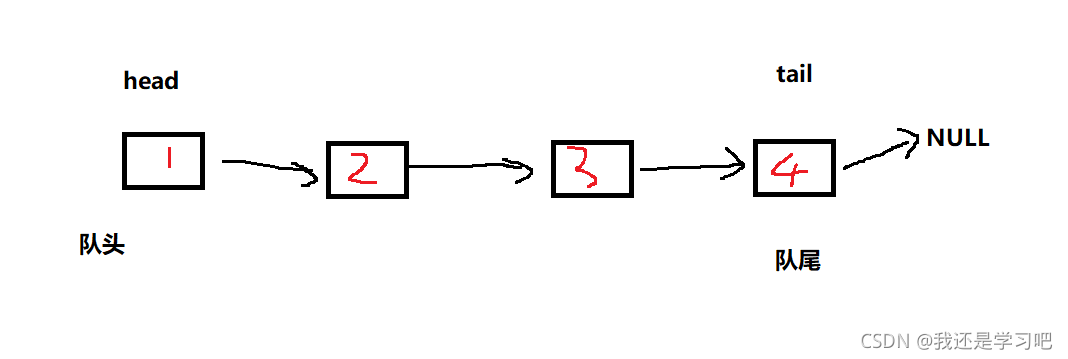
结构定义
//先定义数据类型
typedef int QDataType;
//再定义链表节点
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QueueNode;
//最后定义队列结构
typedef struct Queue
{
QueueNode* head;
QueueNode* tail;
}Queue;
初始化
这里实现的队列也是由使用者定义,传地址给函数将初始化。
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = NULL;
pq->tail = NULL;
}
销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
Queue* cur = pq->head;
while(cur != NULL)
{
Queue* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
入队
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
newnode->data = x;
newnode->next = NULL;
if(pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
}
出队
这里要注意,当队列数据全部出队后,如果不修改tail的指向,则pq->tail便是一个野指针。
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
if(pq->head == NULL)
{
pq->tail = NULL;
}
}
取队头元素
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
取队尾元素
QDatatype QueueBack(Queue* pq)
{
assert(pq):
assert(!QueueEmpty(pq));
return pq->tail->data;
}
计算队列中数据个数
int QueueSize(Queue* pq)
{
assert(pq):
int n = 0;
QueueNode* cur = pq->head;
while(cur)
{
++n;
cur = cur->next;
}
return n;
}
判空
void QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL;
}
总结
实现栈和队列本质上是对顺序表和链表(单链表)的应用。
这里要理解定义结构的思想。