01- 求路径 - js
描述
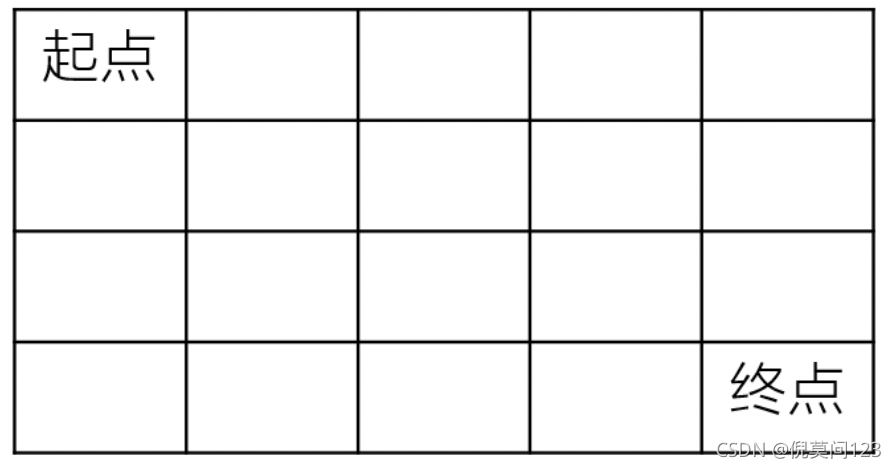
一个机器人在m×n大小的地图的左上角(起点)。
机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
思路:
1.创建一个m * n的数组之后,首先将第一行和第一列的数据全部设置为1(因为从起点出发到达第一行第一列的任意位置都只需要向右走或者向下走,所以走这行和这列的路径只有一条)
2.其他位置的则是由自己当前位置的上边和左边位置的路径之和,因为想到到达当前位置,可以从上边下来,也可以从左边过来。以此类推到表格中的终点即是result[m-1][n - 1]
代码实现:
function uniquePaths( m , n ) {
// write code here
// 1.创建m*n的数组
let dp = []
for(let i = 0; i < m; i ++){
let newArr = new Array(n)
dp.push(newArr)
}
// 2.将二维数组的第一行和第一列的数据设置为1
for(let i = 0; i < dp[0].length; i ++) dp[0][i] = 1 // 设置行
for(let i = 0; i < dp.length; i ++) dp[i][0] = 1 // 设置行
// 3.其他位置的数据是当前位置的上边和左边位置数据的加和
for(let i = 1; i < dp.length; i ++){
for(let j = 1; j < dp[i].length; j ++) dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
}
return dp[m -1][n - 1]
}
02 - 有效括号序列 - js
描述
给出一个仅包含字符’(’,’)’,’{’,’}’,’[‘和’]’,的字符串,判断给出的字符串是否是合法的括号序列
括号必须以正确的顺序关闭,"()“和”()[]{}“都是合法的括号序列,但”(]“和”([)]"不合法。
示例1
输入:"["
返回值:false
示例2
输入:"[]"
返回值:true
思路:
结合栈数据结构的特点,从字符串的头部开始遍历遇见三种括号中的左括号就压栈,遇见右括号就开始弹栈,将栈顶元素取出来和当前位置的字符进行比较,是否能组成一对符合要求的括号,满足要求弹栈,不满足要求压栈,反复操作这两个步骤一直到字符串遍历完之后判断栈中是否还有元素,如果是空栈return true 否则 return false
代码实现:
function isValid( s ) {
// write code here
if(s.length % 2 !== 0) return false
let stack = []
stack.push(s[0])
for(let i = 1 ; i < s.length; i ++){
let stackTopEl = stack[stack.length - 1]
let ce = s[i]
if( stackTopEl === '(' && ce === ')' ||
stackTopEl === '[' && ce === ']' ||
stackTopEl === '{' && ce === '}'){
stack.pop()
}else{
stack.push(ce)
}
}
return stack.length === 0 ? true : false
}
03 - 最长公共前缀 - js
描述
给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。
示例1
输入:["abca","abc","abca","abc","abcc"]
返回值:"abc"
思路:
1.最长公共前缀一定在最短的字符串中出现,所以第一步从字符串数组中找到最短的字符串,通过切割这个字符串的方式来获取最长公共前缀。
代码实现:
function longestCommonPrefix( strs ) {
// write code here
// 如果字符数组的长度是0 或者 1 直接返回相应的值即可
if(strs.length === 0) return ''
else if(strs.length === 1) return strs[0]
let minStrs = strs[0]
// 获取最短字符串
for(let i = 1; i < strs.length; i ++){
if(minStrs.length > strs[i].length) minStrs = strs[i]
}
// 如果最短字符串是空串的话 直接return
if(!minStrs){
return minStrs
}
let flag = true
for(let i = 0; i <= minStrs.length; i ++){
// 开始从长到短切割找到的最短字符串
let withChar = minStrs.slice(0,minStrs.length - i)
for(let j = 0; j < strs.length; j ++){
// 字符串数组中有一项里面不包含 当前缀的退出循环,就行切割
if(!strs[j].includes(withChar)){
flag = false
break
}
}
// 如果都满足的话 就返回切割之后的前缀
if(flag){
return withChar
}else{
flag = true // 不满足的情况下 将return出函数的标志变量初始化,继续切割
}
}
}
04 - 找到搜索二叉树中两个错误的节点 - js
描述
一棵二叉树原本是搜索二叉树,但是其中有两个节点调换了位置,使得这棵二叉树不再是搜索二叉树,请按升序输出这两个错误节点的值。(每个节点的值各不相同)
搜索二叉树:满足每个节点的左子节点小于当前节点,右子节点大于当前节点。

思路 :
1.递归比较(没找到递归的条件所以没写出来)
2.中序遍历得到一个数组,然后查找顺序发生变化的两个位置,就是这两个错误的节点
2.1 两个指针分别从数组的头部和尾部开始移动,向后移动的指针查找当前位置的数据比下一个位置的数据大的,向后移动的指针查找当前位置的数据比前一个位置的数据小的。
2.2 最后将这两个位置的数据放进数组中返回即可。
代码实现:
function findError( root ) {
// write code here
if(root == null) return []
let result = []
function recursive(root){
if(root == null) return
recursive(root.left)
result.push(root.val)
recursive(root.right)
}
recursive(root)
let ans = new Array(2)
let i = 0
let j = result.length
for(i; i < result.length; i ++){
if(result[i] > result[i + 1]) {
ans[1] = result[i]
break
}
}
for(j; j > i; j--){
if(result[j] < result[j - 1]){
ans[0] = result[j]
break
}
}
return ans
}