[数据结构与算法]数据结构哈夫曼树的基本操作（C语言）

目录

//1、树的结构定义

//2、创建哈夫曼树

//3、 根到叶子的路径

?//4、哈夫曼编码

//完整测试源码

//1、树的结构定义

#define n 4	//叶子结点个数
#define m 2*n-1 //树的个数

typedef struct HFTree {
	int weight;	//权值
	int parent;	//双亲
	int left;	//左儿子
	int right;	//右儿子
}*HF;
HF hftree[m+1];	//下标从1开始计数，树的结点都是存在这个数组里的，通过下标来访问

//2、创建哈夫曼树

先将n个带权值的结点看作n个树（只有一个结点的树），再将两个权值最小的树合并在一起形成一棵新树，新树的根节点权值就为左右子树的权值之和，然后让新树继续和没有合并过的树进行合并，直到合并完只剩一棵树，这棵树就是哈夫曼树。

//创建哈夫曼树
void createHftree() {
	//先初始化数组里的所有结点，因为最后合并了树必然会有m个结点
	for (int i = 1; i <= m; i++) {
		hftree[i] = (HF)malloc(sizeof(struct HFTree));
		hftree[i]->weight = 0;
		hftree[i]->left = 0;
		hftree[i]->parent = 0;
		hftree[i]->right = 0;
	}
	//给每个结点赋值权值
    //这里只赋值到下标为n的结点，因为最开始只有n个结点
	for (int i = 1; i <= n; i++) {
		scanf("%d", &hftree[i]->weight);
	}
	//合并树
	for (int i = n + 1; i <= m; i++) {
		//定义两个变量作两个最小权值的结点的下标
		int p1 = 0;
		int p2 = 0;
		//定义两个变量作两个最小的权值
		int s1 = 32767;//32767是16位计算机下最大的int值
		int s2 = 32767;
		//找出最小的两个值
		for (int j = 1; j <= i-1; j++) {
			if (hftree[j]->parent == 0) {//没有双亲结点就表示他还没有被合并
				if (hftree[j]->weight < s1) {
					s2 = s1;
					s1 = hftree[j]->weight;
					p2 = p1;
					p1 = j;
				}
				else if(hftree[j]->weight<s2){
					s2 = hftree[j]->weight;
					p2 = j;
				}
			}
   		}
		//合并操作
		hftree[p1]->parent = i;
		hftree[p2]->parent = i;
		hftree[i]->left = p1;
		hftree[i]->right = p2;
		hftree[i]->weight = hftree[p1]->weight + hftree[p2]->weight;
	}
}

//3、 根到叶子的路径

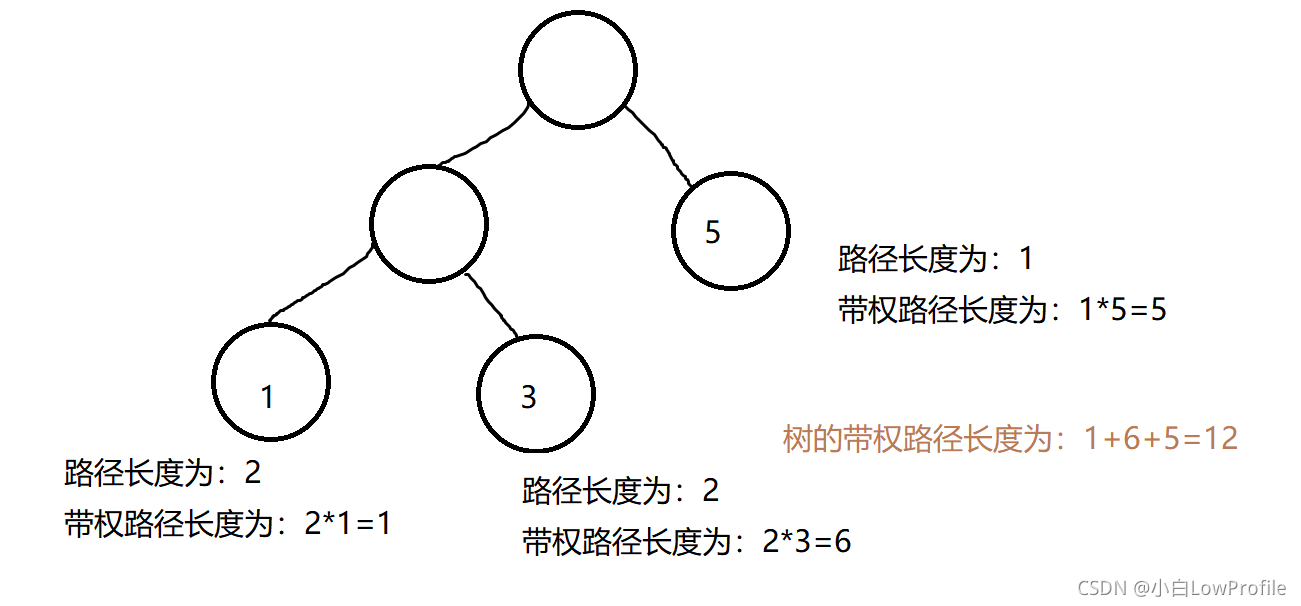
1、路径和路径长度：一棵树中，任意两个结点之间的通路称为路径；通路中分支的数量称为路径长度。

2、权及带权路径长度：权是人为假定的赋值给结点的一个值；从根结点到该结点的? 路径长度*权值? 就是带权路径长度。

3、树的带权路径长度：所有叶子结点的带权路径长度之和为树的带权路径长度。

//根到叶子的路径
//用一个辅助栈
typedef struct PathNode {
	HF stack[m];	//辅助栈
	int top;	//栈顶指针
	int len;	//每一条路径的路径长度
}*PathNode;
PathNode s;
int num = 0;//作树的带权路径
//初始化栈
void init() {
	s->top = -1;
	s->len = -1;
}
//压栈
void Push(HF root) {
	s->stack[++s->top] = root;
	s->len++;
}
//出栈
void Pop() {
	s->top--;
	s->len--;
}
//打印栈
void PrintStack() {
	printf("%d", s->stack[0]->weight);
	int i = 1;
	for (; i <= s->top; ++i) {
		printf("-->%d", s->stack[i]->weight);
	}
	printf("，路径长度为：%d，", s->len);
	printf("带权路径长度为：%d\n", (s->len)*(s->stack[--i]->weight));
	num += (s->len) * (s->stack[i]->weight);//累加树的带权路径
}
//树的路径
void Path(HF root) {
	if (root == NULL)
		return;
	//先把结点压栈
	Push(root);
	//如果是叶子结点就打印栈里的结点
	if (root->left == 0 && root->right == 0)
		PrintStack(); 
	//如果不是，就递归子树
	else {
		Path(hftree[root->left]);
		Path(hftree[root->right]);
	}
	//出栈，改变路径的终点
	Pop();
}

?//4、哈夫曼编码

规定：往左编码为 0 ，往右编码为 1 。

在得到一个结点的编码时，用一个栈暂存编码，结点有左儿子就会递归它的左儿子，所以在此前会往栈里存一个0，如果左子树递归完没有找到目标结点并且栈里有元素的话，那就要退栈，然后回到原来结点递归右儿子，继续上述操作，直到找到了目标结点。

//哈夫曼编码
//用一个辅助栈，用栈来存储编码，向左走就存0，向右就存1
typedef struct Stack {
	int stack[n];	//辅助栈
	int top;	//栈顶指针
}*Stack;
Stack S;
int ok = 0;	//判定变量，为0表示没有找到目标结点
//初始化栈
void init1() {
	S = (Stack)malloc(sizeof(struct Stack));
	S->top = 0;
	ok = 0;	//每一次初始化就顺便给这个变量也初始化了，方便第二次用
}
//哈夫曼编码
void HfCode(HF root,int weight) {    //weight是要编码的结点的权值
	//当结点为空或者结点的权值是目标权值的时候返回
	if (root == NULL || root->weight == weight) {	
		if (root->weight == weight)//如果找到了目标权值的结点
			ok = 1;	//把ok变为1，代表已经找到了要编码的结点
		return;
	}
	//如果没有找到目标结点并且当前结点有左子树
	if (root->left&&ok==0) {
		S->stack[++S->top] = 0;	//因为是向左，所以存0
		HfCode(hftree[root->left], weight);	//然后递归左子树
		if (root->right&&ok==0) {	//如果没有找到目标结点并且当前结点有右子树
			S->stack[++S->top] = 1;	//向右，存1
			HfCode(hftree[root->right], weight);	//递归右子树
		}
	}
	//如果没有找到目标结点并且栈顶指针不为0，就要出栈
	if (ok == 0&&S->top>0)
		S->top--;
}
//打印编码
void PrintCode() {
	for (int i = 1; i <= S->top; i++) {
		printf("%d",  S->stack[i]);
	}
	printf("\n");
}

//完整测试源码

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<malloc.h>

#define n 4	//叶子结点个数
#define m 2*n-1 //树的个数

typedef struct HFTree {
	int weight;	//权值
	int parent;	//双亲
	int left;	//左儿子
	int right;	//右儿子
}*HF;
HF hftree[m+1];	//下标从1开始计数
//创建哈夫曼树
void createHftree() {
	//初始化n个叶子结点
	for (int i = 1; i <= m; i++) {
		hftree[i] = (HF)malloc(sizeof(struct HFTree));
		hftree[i]->weight = 0;
		hftree[i]->left = 0;
		hftree[i]->parent = 0;
		hftree[i]->right = 0;
	}
	//给每个结点赋值权值
	for (int i = 1; i <= n; i++) {
		scanf("%d", &hftree[i]->weight);
	}
	//合并树
	for (int i = n + 1; i <= m; i++) {
		//定义两个变量作两个最小权值的结点的下标
		int p1 = 0;
		int p2 = 0;
		//定义两个变量作两个最小的权值
		int s1 = 32767;
		int s2 = 32767;
		//找出最小的两个值
		for (int j = 1; j <= i-1; j++) {
			if (hftree[j]->parent == 0) {
				if (hftree[j]->weight < s1) {
					s2 = s1;
					s1 = hftree[j]->weight;
					p2 = p1;
					p1 = j;
				}
				else if(hftree[j]->weight<s2){
					s2 = hftree[j]->weight;
					p2 = j;
				}
			}
   		}
		//合并操作
		hftree[p1]->parent = i;
		hftree[p2]->parent = i;
		hftree[i]->left = p1;
		hftree[i]->right = p2;
		hftree[i]->weight = hftree[p1]->weight + hftree[p2]->weight;
	}
}
//菜单
void menu() {
	printf("------------------\n");
	printf("----*哈夫曼树*----\n");
	printf("1、根到叶子的路径\n");
	printf("2、  哈夫曼编码  \n");
	printf("------------------\n");
}
//根到叶子的路径
//用一个辅助栈
typedef struct PathNode {
	HF stack[m];	//辅助栈
	int top;	//栈顶指针
	int len;	//每一条路径的路径长度
}*PathNode;
PathNode s;
int num = 0;//树的带权路径
//初始化栈
void init() {
	s->top = -1;
	s->len = -1;
}
//压栈
void Push(HF root) {
	s->stack[++s->top] = root;
	s->len++;
}
//出栈
void Pop() {
	s->top--;
	s->len--;
}
//打印栈
void PrintStack() {
	printf("%d", s->stack[0]->weight);
	int i = 1;
	for (; i <= s->top; ++i) {
		printf("-->%d", s->stack[i]->weight);
	}
	printf("，路径长度为：%d，", s->len);
	printf("带权路径长度为：%d\n", (s->len)*(s->stack[--i]->weight));
	num += (s->len) * (s->stack[i]->weight);//累加树的带权路径
}
//树的路径
void Path(HF root) {
	if (root == NULL)
		return;
	//先把结点压栈
	Push(root);
	//如果是叶子结点就打印栈里的结点
	if (root->left == 0 && root->right == 0)
		PrintStack(); 
	//如果不是，就递归子树
	else {
		Path(hftree[root->left]);
		Path(hftree[root->right]);
	}
	//出栈，改变路径的终点
	Pop();
}
//哈夫曼编码
//用一个辅助栈，用栈来存储编码，向左走就存0，向右就存1
typedef struct Stack {
	int stack[n];	//辅助栈
	int top;	//栈顶指针
}*Stack;
Stack S;
int ok = 0;	//判定变量
//初始化栈
void init1() {
	S = (Stack)malloc(sizeof(struct Stack));
	S->top = 0;
	ok = 0;	//每一次初始化就顺便给这个变量也初始化了，方便第二次用
}
//哈夫曼编码
void HfCode(HF root,int weight) {
	//当结点为空或者结点的权值是目标权值的时候返回
	if (root == NULL || root->weight == weight) {	
		if (root->weight == weight)//如果找到了目标权值的结点
			ok = 1;	//把ok变为1，代表已经找到了要编码的结点
		return;
	}
	//如果没有找到目标结点并且当前结点有左子树
	if (root->left&&ok==0) {
		S->stack[++S->top] = 0;	//因为是向左，所以存0
		HfCode(hftree[root->left], weight);	//然后递归左子树
		if (root->right&&ok==0) {	//如果没有找到目标结点并且当前结点有右子树
			S->stack[++S->top] = 1;	//向右，存1
			HfCode(hftree[root->right], weight);	//递归右子树
		}
	}
	//如果没有找到目标结点并且栈顶指针不为0，就要出栈
	if (ok == 0&&S->top>0)
		S->top--;
}
//打印编码
void PrintCode() {
	for (int i = 1; i <= S->top; i++) {
		printf("%d",  S->stack[i]);
	}
	printf("\n");
}
//主函数
int main() {
	int elem = 0;	//作要编码的结点的权值
	int chose = 0;
	printf("请输入%d个整数：\n", n);
	createHftree();	//创建哈夫曼
	while (1) {
		menu();
		scanf("%d", &chose);
		switch (chose) {
		case 1:
			s = (PathNode)malloc(sizeof(struct PathNode));
			init();	//初始化辅助栈
			Path(hftree[m]);	//路径
			printf("树的带权路径是：%d\n", num);
			num = 0;	//重置树的带权路径
			break;
		case 2:
			init1();	//初始化辅助栈
			printf("输入要编码的结点的权值：");
			scanf("%d", &elem);
			HfCode(hftree[m],elem);	//编码
			printf("权值为%d的结点的编码是：", elem);
			PrintCode();	//打印
			break;
		default:return;
		}
	}
	return 0;
}