[数据结构与算法]剑指 Offer——第二十天（重建二叉树）

第一题：剑指 Offer 07. 重建二叉树

问题描述

思路

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        if(n == 0) return null;
        int rootVal = preorder[0],Index = 0;
        for(int i=0;i<n;i++){
            if(rootVal == inorder[i]){
                Index = i;
                break;
            }
        }
        TreeNode root = new TreeNode(rootVal);
        root.left = buildTree(Arrays.copyOfRange(preorder, 1, 1 + Index), 
        Arrays.copyOfRange(inorder, 0, Index));
        root.right = buildTree(Arrays.copyOfRange(preorder, 1 + Index, n), 
        Arrays.copyOfRange(inorder, Index + 1, n));

        return root;
    }
}

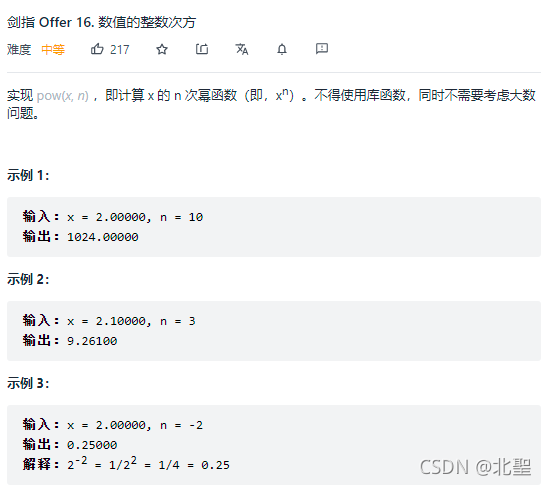
第二题：剑指 Offer 16. 数值的整数次方

问题描述

思路

代码

class Solution {
    public double myPow(double x, int n) {
        if(n == 0) return 1;
        if(n == 1) return x;
        if(n == -1) return 1/x;
        double half = myPow(x , n / 2);
        double mod = myPow(x , n % 2);
        return half*mod*half;
    }
}

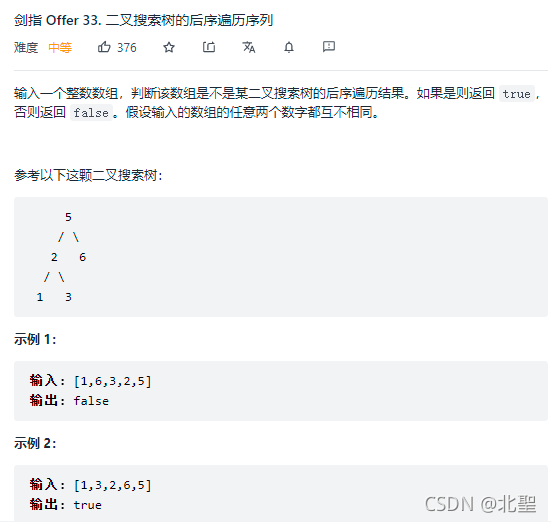
第三题：剑指 Offer 33. 二叉搜索树的后序遍历序列

问题描述

思路

借鉴一下大佬思路
解题思路：
后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。
二叉搜索树定义： 左子树中所有节点的值 << 根节点的值；右子树中所有节点的值 >> 根节点的值；其左、右子树也分别为二叉搜索树。

方法一：递归分治
根据二叉搜索树的定义，可以通过递归，判断所有子树的 正确性 （即其后序遍历是否满足二叉搜索树的定义） ，若所有子树都正确，则此序列为二叉搜索树的后序遍历。
递归解析：
终止条件： 当 i \geq ji≥j ，说明此子树节点数量 \leq 1≤1 ，无需判别正确性，因此直接返回 truetrue ；
递推工作：
划分左右子树： 遍历后序遍历的 [i, j][i,j] 区间元素，寻找 第一个大于根节点 的节点，索引记为 mm 。此时，可划分出左子树区间 [i,m-1][i,m?1] 、右子树区间 [m, j - 1][m,j?1] 、根节点索引 jj 。
判断是否为二叉搜索树：
左子树区间 [i, m - 1][i,m?1] 内的所有节点都应 << postorder[j]postorder[j] 。而第 1.划分左右子树 步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
右子树区间 [m, j-1][m,j?1] 内的所有节点都应 >> postorder[j]postorder[j] 。实现方式为遍历，当遇到 \leq postorder[j]≤postorder[j] 的节点则跳出；则可通过 p = jp=j 判断是否为二叉搜索树。
返回值： 所有子树都需正确才可判定正确，因此使用 与逻辑符 &&&& 连接。
p = jp=j ： 判断 此树 是否正确。
recur(i, m - 1)recur(i,m?1) ： 判断 此树的左子树 是否正确。
recur(m, j - 1)recur(m,j?1) ： 判断 此树的右子树 是否正确。

作者：jyd
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/solution/mian-shi-ti-33-er-cha-sou-suo-shu-de-hou-xu-bian-6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码

class Solution {
    // 要点：二叉搜索树中根节点的值大于左子树中的任何一个节点的值，小于右子树中任何一个节点的值，子树也是
    public boolean verifyPostorder(int[] postorder) {
        if (postorder.length < 2) return true;
        return verify(postorder, 0, postorder.length - 1); 
    }

    // 递归实现
    private boolean verify(int[] postorder, int left, int right){
        if (left >= right) return true; // 当前区域不合法的时候直接返回true就好

        int rootValue = postorder[right]; // 当前树的根节点的值

        int k = left;
        while (k < right && postorder[k] < rootValue){ // 从当前区域找到第一个大于根节点的，说明后续区域数值都在右子树中
            k++;
        }

        for (int i = k; i < right; i++){ // 进行判断后续的区域是否所有的值都是大于当前的根节点，如果出现小于的值就直接返回false
            if (postorder[i] < rootValue) return false;
        }

        // 当前树没问题就检查左右子树
        if (!verify(postorder, left, k - 1)) return false; // 检查左子树

        if (!verify(postorder, k, right - 1)) return false; // 检查右子树

        return true; // 最终都没问题就返回true
    }
}