目录
初遇🌖(数据结构是什么?)
我:嗨,你好!数据结构,你是谁?
她:我是计算机存储、组织数据的方式;具体来说就是指相互之间存在一种或多种特定关系的数据元素的集合!
我:阁下当真是计算机江湖中的最强女侠!
她:不敢当,小兄弟。我还有一个闺蜜和我共闯江湖!
我:敢问她是?
算法·出现🌗
她:她是算法(Algorith),就是定义良好的计算过程,她取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说,算法就是一系列的计算步骤,用来将输入数据转化为输出的结果。
算法·效率🌘
江湖中,传闻,算法效率有时空之分,具体来说便是时间效率与空间效率之分
时间效率被称为时间复杂度——衡量一个算法的运行速度
空间效率被称为空间复杂度——衡量一个算法所需的额外空间
在计算机发展早期,计算机存储容量很小,所以很在意空间复杂度;但是时光流逝,如今计算机的江湖之中,存储容量已到达极之巅峰,我们已无需特别关注算法复杂度了
时间复杂度🌕
·时间复杂度的身世🙋?♂?
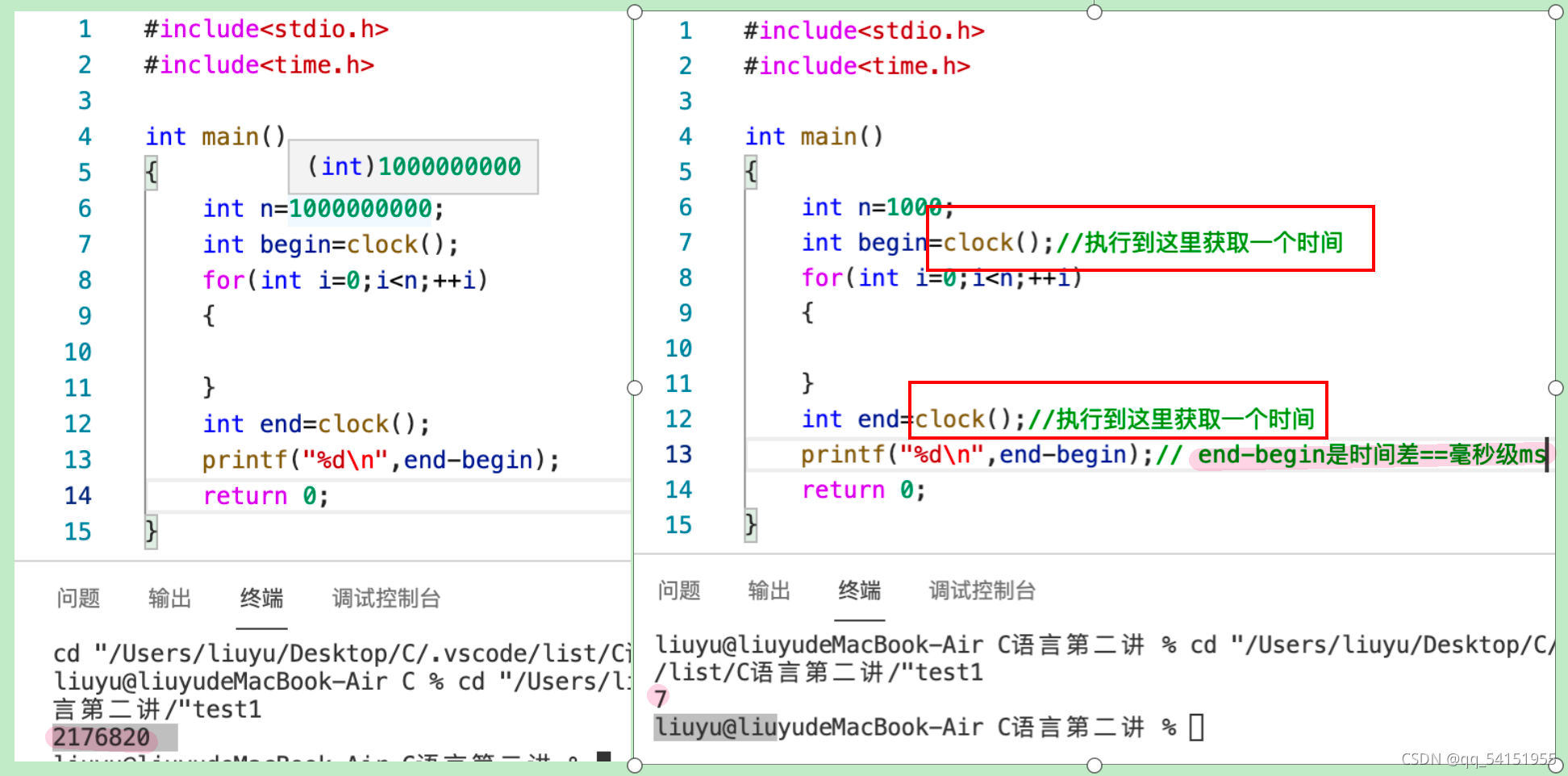
算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。
一个算法所花费的时间与其中语句的执行次数成正比,算法中的基本操作的执行次数,为算法的时间复杂度
·大O的渐进表示法🤳
实际中我们计算时间复杂度只需要计算大概执行次数,那么我们使用大O的渐进表示法。
大O符号:用于描述函数渐进式行为的数学符号
推导大O阶方法:
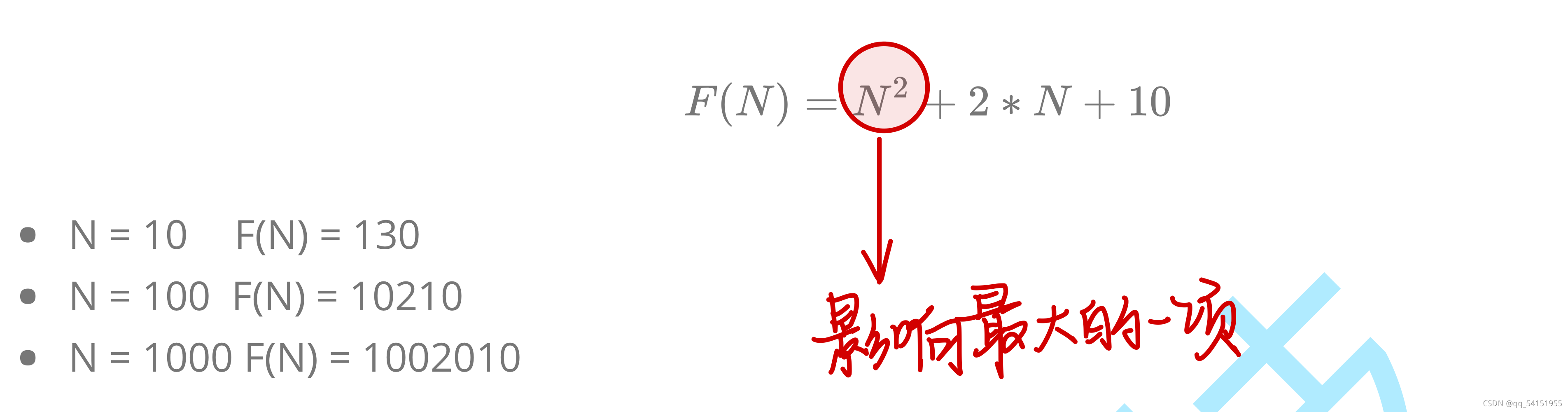
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
时间复杂度身世之别🌟
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
案例1
案例2
案例3 .strchr
案例4.冒泡排序
案例5.二分查找
?时间复杂度中,习惯将log2(N) 简写为 logN
案例6.阶乘递归
案例7.斐波那契递归
?
?
空间复杂度
她的身世
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
案例1.冒泡排序
案例2.斐波那契数组
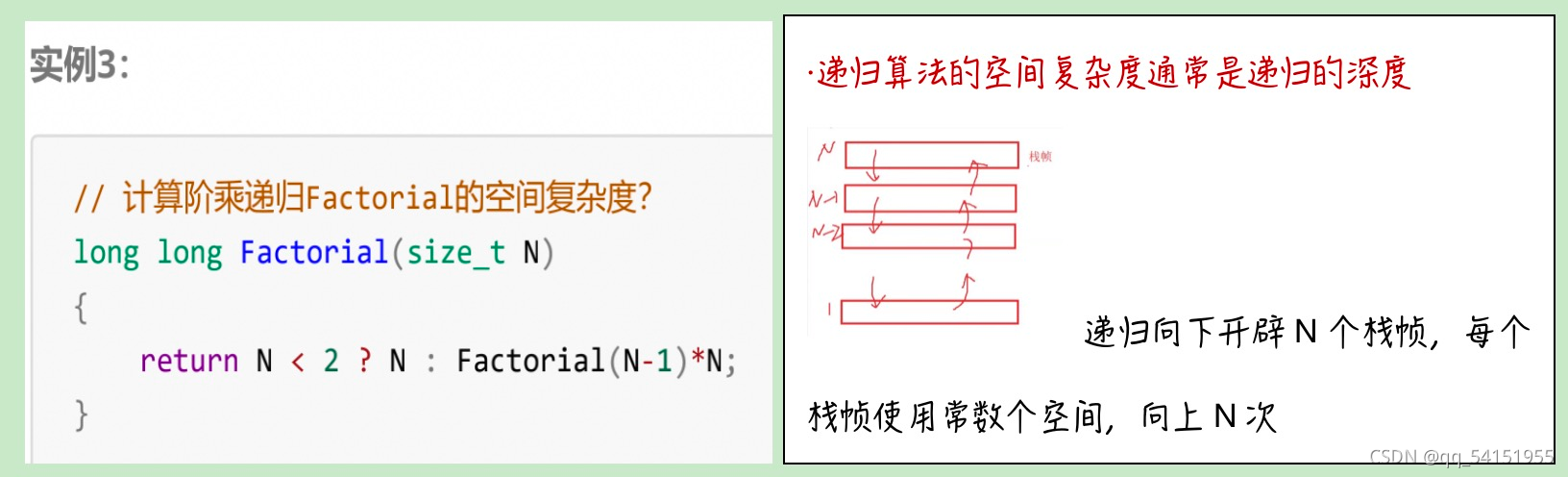
案例3.阶乘递归?
?
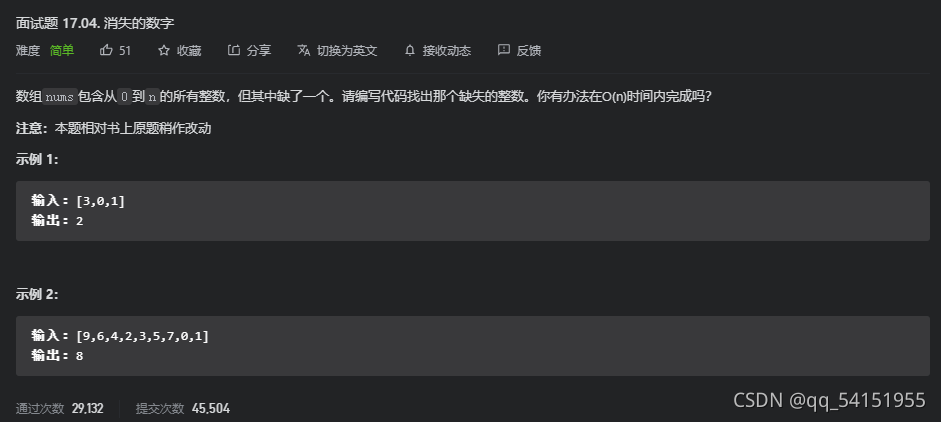
leetcode 面试题17.04 消失的数字
?思路1-排序
采用冒泡排序——?时间复杂度:O(N^2)
采用快排qsort——时间复杂度:O(N*logN)
以上算法时间复杂度均未满足
思路2-数列和
(0-n计算等差数列的和)-(数组中的值相加)
? ? ? ?O(1)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? O(N)?
算法时间复杂度满足√
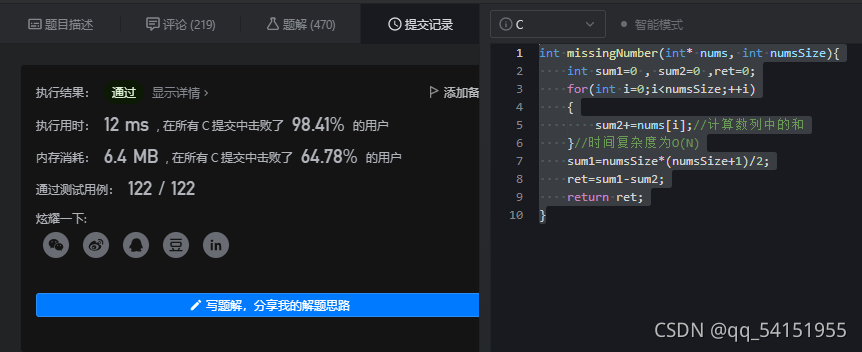
具体实现:
int missingNumber(int* nums, int numsSize){ int sum1=0 , sum2=0 ,ret=0; for(int i=0;i<numsSize;++i) { sum2+=nums[i];//计算数列中的和 }//时间复杂度为O(N) sum1=numsSize*(numsSize+1)/2;//计算0-n的等差数列之和 ret=sum1-sum2; return ret; }
?
思路3-异或^
前情提要:对于一组数字,不论其中的异或顺序,只要在对这组数字异或过程中有两个相同,那么这两个数组异或的最终结果为0
对于本题,可先对0-n的连续数字异或一遍,接着对含有欠缺数字的数组中的每个数字异或,那么该数组中未欠缺的数字和0-n连续数字会异或2次,结果为0;而因为缺少1位数字,原先0-n的连续数字中必有1位只参与了异或1次,即为本身,得解。