题目描述
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是 beginWord 。
- 序列中最后一个单词是 endWord 。
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList,找到从 beginWord 到 endWord 的 最短转换序列 中的单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出:5
解释:一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。
示例 2:
输入:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出:0
解释:endWord “cog” 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10endWord.length == beginWord.length1 <= wordList.length <= 5000wordList[i].length == beginWord.lengthbeginWord、endWord 和 wordList[i] 由小写英文字母组成beginWord != endWordwordList 中的所有字符串 互不相同
问题分析
以第一个示例为例进行分析:
- beginWord = “hit”
- endWord = “cog”
- wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
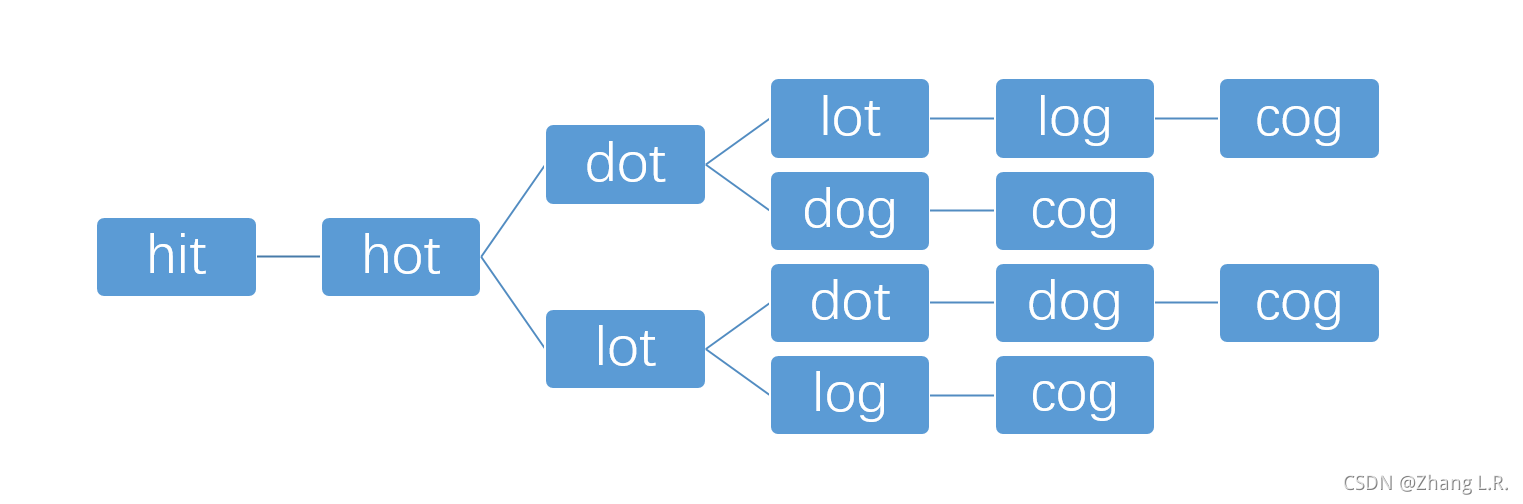
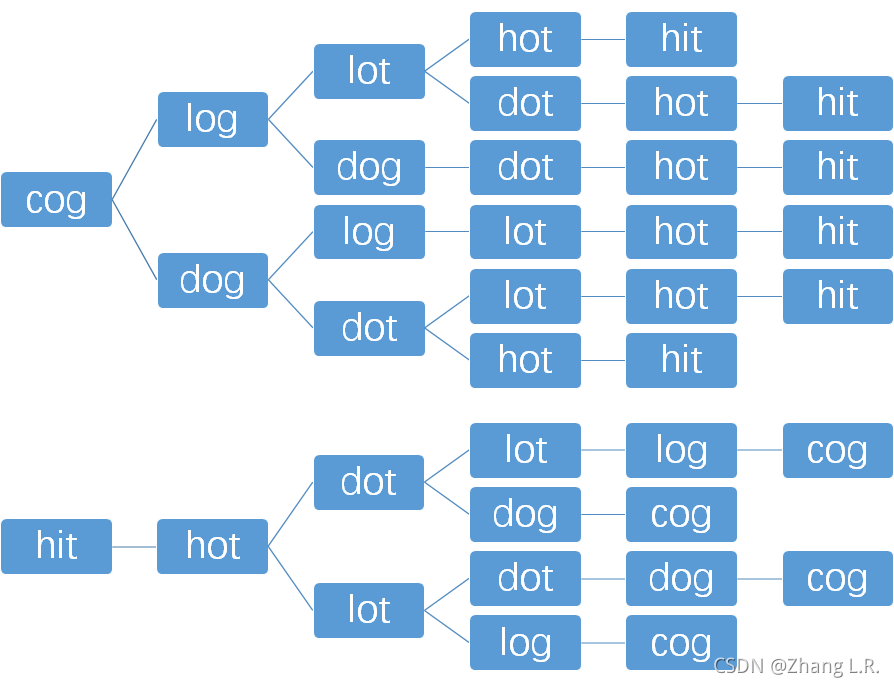
如上图所示,可将该问题抽象为一个图,那么要找到 beginWord 到 endWord 的最短转换序列的单子数量,只需要进行一次BFS检索即可。
解决方案一:单向BFS
按照上图的规则进行广搜遍历即可:
最初代码如下:
/**
* 解题思路:
* 使用level记录当前遍历到了第几层
* 用map标记上一层使用到的单词,在本层中不可重复使用
* 写一个函数来检查两个单词是不是只差一个字符,返回一个boolean
*
* @param beginWord
* @param endWord
* @param wordList
* @return
*/
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// bfs的深度
int level = 0;
// 检查endWord是不是包含在wordList中
if (!wordList.contains(endWord)) {
return 0;
}
// 标记单词是不是已经使用过
Set<String> map = new HashSet<>();
Set<String> tmpMap = new HashSet<>();
// 定义一个Queue来实现bfs
Queue<String> queue = new ArrayDeque<>();
queue.add(beginWord);
while (!queue.isEmpty()) {
/** 从前向后 */
int count = queue.size();
level++;
// 将上一层bfs使用过的单词,在该层统一进行标记
map.addAll(tmpMap);
tmpMap.clear();
while (--count >= 0) {
// 拿出queue中的元素,并在list中查找与其仅有一个字符不同的单词
String key = queue.remove();
// 将key临时记录,并在当前循环结束之后放入map中记录,之后不再访问
tmpMap.add(key);
// 便利整个wordList,找到key可以通过一次变换得到的单词,如果该单词未被访问过,将其放入队列中
for (String s : wordList) {
// 比较key和list中未曾访问过的某个元素是不是仅有一个字符不同
if (!map.contains(s) && checkDiff(key, s)) {
queue.add(s);
// 当前元素s等于endWord的时候,返回即可
if (s.equals(endWord)) {
return level + 1;
}
}
}
}
}
return 0;
}
/**
* 检查key和s是不是只有一个字符不相同
* @param key
* @param str
* @return 满足条件则返回true,否则返回false
*/
private boolean checkDiff(String key, String str) {
if (key == null || str == null) {
return false;
}
int count = 0;
int keyLen = key.length();
int strLen = str.length();
if (keyLen != strLen) {
return false;
}
for (int i = 0; i < keyLen; i++) {
if (key.charAt(i) != str.charAt(i)) {
count++;
if (count > 1) {
return false;
}
}
}
return count == 1;
}
在leetcode提交后,超时
该方法未进行任何优化,时间复杂度极高。可以进行初步优化:
- 检索key通过变化一个字符可变成的单词的时候,在全部wordList中检索,此处可以通过构建一个map存放key可以转化成的单词列表,比如用 Map<String, Set< String>> 来存储。
优化后的代码如下:
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// bfs的深度
int level = 0;
wordList.add(beginWord);
// 检查endWord是不是包含在wordList中
if (!wordList.contains(endWord)) {
return 0;
}
// 将数据进行初始化,用Map<String, Set<String>>来存储一个单词可通过改变一个字符转变成的单词集合
Map<String, Set<String>> wordMap = new HashMap<>();
for (String s: wordList) {
Set<String> set = new HashSet<>();
for (String ss : wordList) {
if (checkDiff(ss, s)) {
set.add(ss);
}
}
wordMap.put(s, set);
}
// 标记单词是不是已经使用过
Set<String> map = new HashSet<>();
Set<String> tmpMap = new HashSet<>();
// 定义一个Queue来实现bfs
Queue<String> queue = new ArrayDeque<>();
queue.add(beginWord);
while (!queue.isEmpty()) {
/** 从前向后 */
int count = queue.size();
level++;
// 将上一层bfs使用过的单词,在该层统一进行标记
map.addAll(tmpMap);
tmpMap.clear();
while (--count >= 0) {
// 拿出queue中的元素,并在list中查找与其仅有一个字符不同的单词
String key = queue.remove();
// 将key临时记录,并在当前循环结束之后放入map中记录,之后不再访问之
tmpMap.add(key);
// 在Map中获取与当前单词key直接相连的单词
Set<String> list = wordMap.get(key);
for (String s : list) {
// 找到list中未曾访问过的某个元素
if (!map.contains(s)) {
// 将s添加到队列中
queue.add(s);
if (s.equals(endWord)) {
return level + 1;
}
}
}
}
}
return 0;
}
/**
* 检查key和s是不是只有一个字符不相同
*
* @param key
* @param str
* @return 满足条件则返回true,否则返回false
*/
private boolean checkDiff(String key, String str) {
if (key == null || str == null) {
return false;
}
int keyLen = key.length();
int strLen = str.length();
if (keyLen != strLen) {
return false;
}
int count = 0;
for (int i = 0; i < keyLen; i++) {
if (key.charAt(i) != str.charAt(i)) {
count++;
if (count > 1) {
return false;
}
}
}
return count == 1;
}
该代码提交通过,运行时间为:

那么对该算法再次进行优化,从endWord开始向前遍历,其逆向的图与正向图的对比如下所示:
那么我们把正向搜索用的队列记为:queueBegin,而逆向搜索的队列记为:queueEnd。那么程序运行过程中,当其中一个队列的元素出现在另一个队列中的时候,结束并返回即可。
按照上述方式优化之后的结果:

另外一个可以优化的地方:
上边的方案中,我是在的另一个队列中检索当前BFS的节点是否存在,那么从上图可以看出来,队列中存在大量的冗余元素,且Queue的检索效率为线性的。另外,我们知道HashSet的查询效率是非常高的,而且还可以去重。那么可以使用两个Set集合来记录当前queueBegin和queueEnd中的元素,以提高检索(队列1中的元素出现在队列2中)效率。
优化后的代码如下:
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// 两个bfs的深度
int level = 0;
wordList.add(beginWord);
// 检查endWord是不是包含在wordList中
if (!wordList.contains(endWord)) {
return 0;
}
// 将数据进行初始化,用Map<String, Set<String>>来存储一个单词可通过改变一个字符转变成的单词集合
Map<String, Set<String>> wordMap = new HashMap<>();
for (String s: wordList) {
Set<String> set = new HashSet<>();
for (String ss : wordList) {
if (checkDiff(ss, s)) {
set.add(ss);
}
}
wordMap.put(s, set);
}
// 标记单词是不是已经使用过 - 从begin处向后
Set<String> usedBegin = new HashSet<>();
// 标记单词是不是已经使用过 - 从end处向前
Set<String> usedEnd = new HashSet<>();
// 定义一个Queue来实现bfs
Queue<String> queueBegin = new ArrayDeque<>();
Queue<String> queueEnd = new ArrayDeque<>();
queueEnd.add(endWord);
queueBegin.add(beginWord);
usedBegin.add(beginWord);
usedEnd.add(endWord);
while (!queueBegin.isEmpty() && !queueEnd.isEmpty()) {
level++;
/** 两个队列,哪个短则让哪个往后搜 */
if (queueBegin.size() > queueEnd.size()) {
Queue<String> tmp = queueBegin;
queueBegin = queueEnd;
queueEnd = tmp;
Set<String> set = usedBegin;
usedBegin = usedEnd;
usedEnd = set;
}
int count = queueBegin.size();
while (--count >= 0) {
// 拿出queue中的元素,并在list中查找与其仅有一个字符不同的单词
String key = queueBegin.remove();
Set<String> list = wordMap.get(key);
if (list == null) {
continue;
}
for (String s : list) {
// 判断s是不是被使用过,使用过则跳过
if (usedBegin.contains(s)) {
continue;
}
// 判断在另一侧的queue中是不是包含
if (queueEnd.contains(s)) {
return level + 1;
}
// 将s添加到队列中
queueBegin.add(s);
usedBegin.add(s);
}
}
}
return 0;
}
/**
* 检查key和s是不是只有一个字符不相同
*
* @param key
* @param str
* @return 满足条件则返回true,否则返回false
*/
private boolean checkDiff(String key, String str) {
if (key == null || str == null) {
return false;
}
int keyLen = key.length();
int strLen = str.length();
if (keyLen != strLen) {
return false;
}
int count = 0;
for (int i = 0; i < keyLen; i++) {
if (key.charAt(i) != str.charAt(i)) {
count++;
if (count>1){
return false;
}
}
}
return count == 1;
}
运行结果(还是很高的,在建立wordMap结构的时间复杂度
O
(
n
2
)
O(n^2)
O(n2)起步):

最终优化方案:
看题解,在单词比对的时候使用了优化,具体思路是:
因为单词是由 a~z 这有限数量的字符组成的,可以遍历当前单词能转换成的所有单词,判断其是否包含在候选单词列表wordList中。
代码实现
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// 两个bfs的深度
int level = 0;
wordList.add(beginWord);
Set<String> wordListSet = new HashSet<>(wordList);
// 检查endWord是不是包含在wordList中
if (!wordList.contains(endWord)) {
return 0;
}
// 将数据进行初始化,用Map<String, Set<String>>来存储一个单词可通过改变一个字符转变成的单词集合
Map<String, Set<String>> wordMap = new HashMap<>();
for (String s: wordList) {
Set<String> set = new HashSet<>();
char[] ss = s.toCharArray();
for (int i = 0; i < ss.length; i++) {
char tmpc = ss[i];
for (char c = 'a'; c <= 'z'; c++) {
ss[i] = c;
String str = new String(ss);
if (wordListSet.contains(str)) {
set.add(str);
}
}
ss[i] = tmpc;
}
wordMap.put(s, set);
}
// 标记单词是不是已经使用过 - 从begin处向后
Set<String> usedBegin = new HashSet<>();
// 标记单词是不是已经使用过 - 从end处向前
Set<String> usedEnd = new HashSet<>();
// 定义一个Queue来实现bfs
Queue<String> queueBegin = new ArrayDeque<>();
Queue<String> queueEnd = new ArrayDeque<>();
queueEnd.add(endWord);
queueBegin.add(beginWord);
usedBegin.add(beginWord);
usedEnd.add(endWord);
while (!queueBegin.isEmpty() && !queueEnd.isEmpty()) {
level++;
/** 两个队列,哪个短则让哪个往后搜 */
if (queueBegin.size() > queueEnd.size()) {
Queue<String> tmp = queueBegin;
queueBegin = queueEnd;
queueEnd = tmp;
Set<String> set = usedBegin;
usedBegin = usedEnd;
usedEnd = set;
}
int count = queueBegin.size();
while (--count >= 0) {
// 拿出queue中的元素,并在list中查找与其仅有一个字符不同的单词
String key = queueBegin.remove();
Set<String> list = wordMap.get(key);
if (list == null) {
continue;
}
for (String s : list) {
// 判断s是不是被使用过,使用过则跳过
if (usedBegin.contains(s)) {
continue;
}
// 判断在另一侧的queue中是不是包含
if (queueEnd.contains(s)) {
return level + 1;
}
// 将s添加到队列中
queueBegin.add(s);
usedBegin.add(s);
}
}
}
return 0;
}
运行结果:

其实,可以不用构建wordMap,直接将其嵌入到循环中的话,效率其实也挺高的。因为在循环中的话,不需要对每个单词都进行检索一次,只会对那些从队列中取出来的元素检索。
代码:
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// 两个bfs的深度
int level = 0;
wordList.add(beginWord);
Set<String> wordListSet = new HashSet<>(wordList);
// 检查endWord是不是包含在wordList中
if (!wordList.contains(endWord)) {
return 0;
}
// 标记单词是不是已经使用过 - 从begin处向后
Set<String> usedBegin = new HashSet<>();
// 标记单词是不是已经使用过 - 从end处向前
Set<String> usedEnd = new HashSet<>();
// 定义一个Queue来实现bfs
Queue<String> queueBegin = new ArrayDeque<>();
Queue<String> queueEnd = new ArrayDeque<>();
queueEnd.add(endWord);
queueBegin.add(beginWord);
usedBegin.add(beginWord);
usedEnd.add(endWord);
while (!queueBegin.isEmpty() && !queueEnd.isEmpty()) {
level++;
/** 两个队列,哪个短则让哪个往后搜 */
if (queueBegin.size() > queueEnd.size()) {
Queue<String> tmp = queueBegin;
queueBegin = queueEnd;
queueEnd = tmp;
Set<String> set = usedBegin;
usedBegin = usedEnd;
usedEnd = set;
}
int count = queueBegin.size();
while (--count >= 0) {
// 拿出queue中的元素,并在list中查找与其仅有一个字符不同的单词
String key = queueBegin.remove();
char[] keys = key.toCharArray();
for (int i = 0; i < keys.length; i++) {
char tmp = keys[i];
for (char c = 'a'; c <= 'z'; c++) {
keys[i] = c;
String tmps = new String(keys);
if (usedBegin.contains(tmps)) {
continue;
}
if (usedEnd.contains(tmps)) {
return level + 1;
}
if (wordListSet.contains(tmps)) {
queueBegin.add(tmps);
usedBegin.add(tmps);
}
}
keys[i] = tmp;
}
}
}
return 0;
}
这种优化之后,运行速度: