平衡二叉树(Balanced Binary Tree)
平衡二叉树(Balanced Binary Tree)又称AVL树。AVL 树得名于它的发明者 G. M. Adelson-Velsky 和 Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。这种结构完成一系列集合操作时,时间复杂度与空间复杂度比其他树要低,一系列操作始终保持平衡!为大型数据库的组织、索引提供了一条全新的的道路!
1、BST树的不足
现给定一组有序数列[1, 2, 3, 4, 5, 6],要求创建一颗二叉排序树(BST),并分析问题所在!
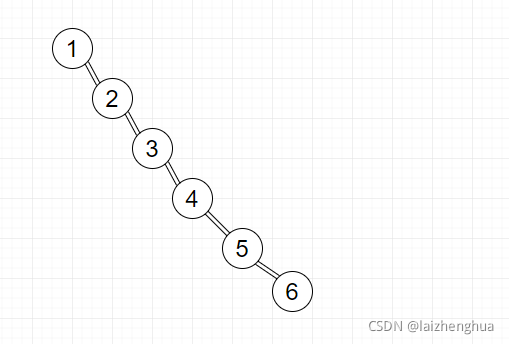
由数列[1, 2, 3, 4, 5, 6]构成的BST树如上图所示。那么这棵树存在的问题有以下几点:
1、左子树全部为空,从形式上看,更像一个单链表,实际上已经退化成一个单链表了
2、对于插入、删除、修改速度是没有影响,但是这种结构查询效率会明显降低(因为需要依次比较)不能发挥BST的优势,因为每次还需要比较左子树,器查询速度比单链表还慢。
因此为了解决二叉排序树(BST)退化成链表的问题,出现了一种全新的树结构(AVL树),这种结构不仅能防止退化成单链表,还在插入,查找,删除得到了进一步的改善,所使用的时间复杂度和空间复杂度相较于其他树更低!
2、AVL树介绍
1、平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树,可以保证查询效率较高。
2、具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL算法、替罪羊树、Treap、伸展树等。
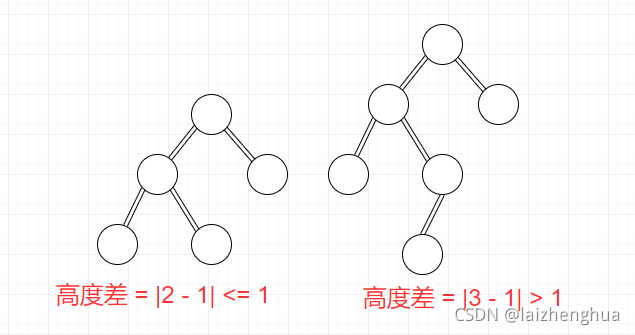
如上图左边就是一颗平衡会二叉树(AVL树),需要注意的是:平衡二叉树必须是一颗二叉排序树(BST),在BST树的基础上满足左右两个子树的高度差的绝对值不超过 1。