鲸鱼优化算法概述
鲸鱼优化算法( Whale Optimization Algorithm,WOA)是 Mirjalili 等于 2016 年提出的一种基于座头鲸鱼狩猎方法的元启发式算法。它成功应用于各种复杂的离散优化问题,如资源调度问题、建筑工地的工作流程规划、选址与路径规划和神经网络训练等。在算法改进和应用方面,闫旭等提出了混合随机量子鲸鱼优化算法求解 TSP 问题; 滕德云等把鲸鱼优化算法与拓扑结构相结合地改进鲸鱼优化算法,用来求解多目标无功优化调度问题; 涂春梅等提出了混沌反馈自适应鲸鱼优化算法; 刘竹松等提出了正余混沌双弦鲸鱼优化算法( CSCWOA) ; 钟明辉等提出了一种随机调整控制参数的高效的鲸鱼优化算法
WOA
WOA 可以用来求解连续性优化问题。因此,本文通过对锦州市多家快递公司的快递配送情况进行调研,结果发现客户满意度和配送效率不尽理想,主要原因在于每个客户点在接受快件的时间段不同,造成快递员的来回奔波和不必要的时间等待,不仅大大降低了快递员配送效率,同时也使客户满意度大打折扣。因此,本文将贪婪交换机制引入到鲸鱼优化算法中,通过建立基于贪婪鲸鱼优化算法( GWOA) 的带时间窗的快递末端配送路径模型,并对实例进行求解,结果证明 GWOA 具有更好的收敛速度和更佳的局部寻优能力。
快递末端配送
路径问题的描述快递末端配送路径问题可以描述为: 快递员从配送中心( 快递配送网点) 出发,沿特定路线将客户的商品送到每个客户点手中,然后需要在固定时间前返回到出发点( 快递配送网点) 。在此期间快递员可以根据自己的经验选择距离较短、节约时间的路线来完成快递的配送,也可以根据某些客户的特殊需求,优先给他们进行配送,前提是保证所有的客户点在指定时间前都被服务到并且只能被服务一次。因此应合理规划快递末端配送路径,在满足客户时间窗、客户需求、配送车辆载重限制、快递车辆最大行驶距离等约束条件下,实现配送时间最短、配送路线距离最短、配送成本最低、客户满意度最大等。
tic
clear
clc
%% 用importdata这个函数来读取文件
data=importdata('input.txt');
cap=160;
%% 提取数据信息
vertexs=data(:,2:3); %所有点的坐标x和y
customer=vertexs(2:end,:); %顾客坐标
cusnum=size(customer,1); %顾客数
v_num=3; %初始车辆使用数目
demands=data(2:end,4); %需求量
h=pdist(vertexs);
dist=squareform(h); %距离矩阵
%% 鲸鱼优化算法参数
NIND=100; %种群数目
MAXGEN=300; %最大迭代次数
N=cusnum+v_num-1; %鲸鱼个体长度=顾客数目+车辆最多使用数目-1
belta=10; %违反装载量约束的惩罚函数系数
%% 种群初始化
init_vc=init(cusnum,demands,cap,dist); %构造OVRP初始解
population=init_pop(NIND,N,cusnum,init_vc);
%% 输出随机解的路线和总距离
obj=obj_function(population,cusnum,cap,demands,dist,belta);
[min_obj,min_index]=min(obj);
disp('初始种群中的最优个体:')
[currVC,NV,TD,violate_num,violate_cus]=decode(population(min_index,:),cusnum,cap,demands,dist); %对初始解解码
disp(['车辆使用数目:',num2str(NV),',车辆行驶总距离:',num2str(TD),',违反约束路径数目:',num2str(violate_num),',违反约束顾客数目:',num2str(violate_cus)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 主循环
gen=1; %计数器初始化
bestInd=population(min_index,:); %初始化全局最优个体
bestObj=min_obj; %初始全局最优个体目标函数值
BestPop=zeros(MAXGEN,N); %记录每次迭代过程中全局最优个体
BestObj=zeros(MAXGEN,1); %记录每次迭代过程中全局最优个体的目标函数值
BestTD=zeros(MAXGEN,1); %记录每次迭代过程中全局最优个体的总距离
while gen<=MAXGEN
%% 更新鲸鱼种群位置
for i=1:NIND
p=rand; %0~1之间的随机数
if p<0.5
population(i,:)=cross1(population(i,:),bestInd,cusnum,cap,demands,dist,belta);
elseif p>=0.5
population(i,:)=cross2(population(i,:),bestInd,cusnum,cap,demands,dist,belta);
end
end
%% 局部搜索操作
population=local_search(population,cusnum,cap,demands,dist,belta);
%% 计算当前鲸鱼种群目标函数值
obj=obj_function(population,cusnum,cap,demands,dist,belta);
[min_obj,min_index]=min(obj);
minInd=population(min_index,:);
%% 更新全局最优鲸鱼个体
if min_obj<bestObj
bestInd=minInd;
bestObj=min_obj;
end
BestPop(gen,:)=bestInd;
BestObj(gen,1)=bestObj;
%% 显示当前全局最优鲸鱼个体解码出的配送方案信息
disp(['第',num2str(gen),'代全局最优解:'])
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestInd,cusnum,cap,demands,dist);
disp(['车辆使用数目:',num2str(bestNV),',车辆行驶总距离:',num2str(bestTD),',违反约束路径数目:',num2str(best_vionum),',违反约束顾客数目:',num2str(best_viocus)]);
fprintf('\n')
BestTD(gen,1)=bestTD;
%% 更新计算器
gen=gen+1;
end
%% 打印外层循环每次迭代的全局最优解的总成本变化趋势图
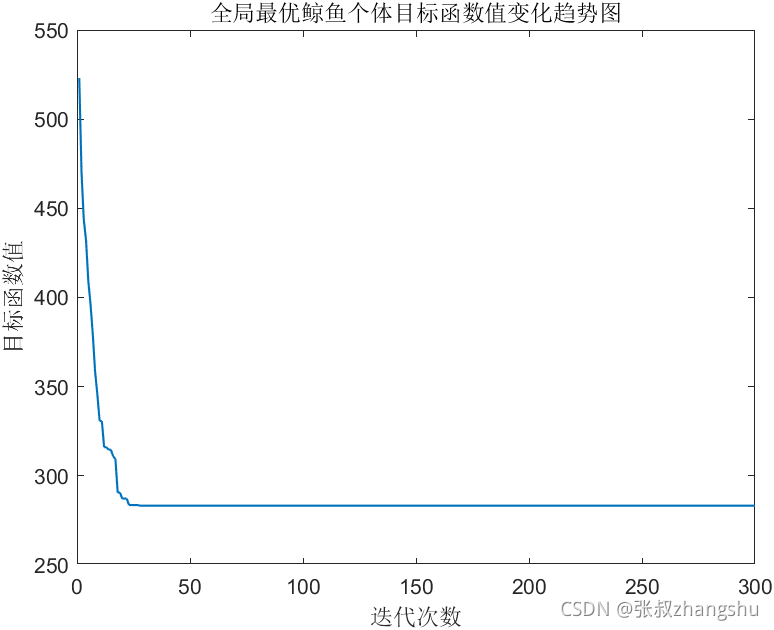
figure;
plot(BestObj,'LineWidth',1);
title('全局最优鲸鱼个体目标函数值变化趋势图')
xlabel('迭代次数');
ylabel('目标函数值');
%% 打印全局最优解路线图,1表示满足,0表示不满足
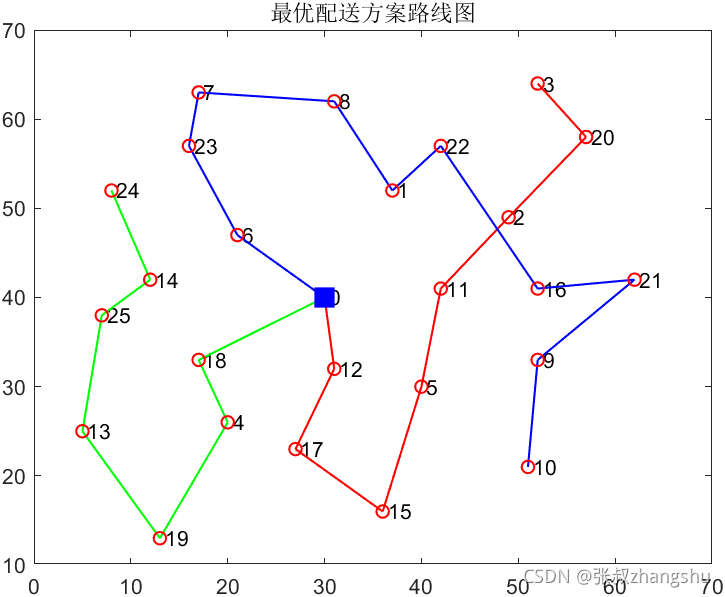
draw_Best(bestVC,vertexs);
toc