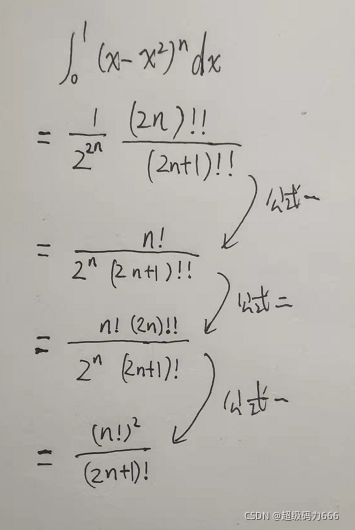2020牛客暑期多校训练营(第一场) J Easy Integration 题
网上题解大多是 不断分部积分求解,其实有更为简洁的解法.
便是 Wallis积分(点火公式) + 组合数学 求解,本文给出思路及过程
题面如下.

(一)为什么会想到 Wallis积分
题意是给出整数 n ,求出下面定积分的值.
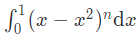
既然给出 n 可求得结果,可知结果与变量x无关.并且见到型如(a-x2)的结构可联想到三角换元,
只不过这里的a非常量而是x.
综合 积分结果与x无关和三角换元的特征,可以想到高等数学中的Wallis积分 (即点火公式)
证明可见同济7版高数上p253例12,这里直接给出公式

(二)计算思路及过程
(1)三角换元→凑微分→Wallis积分
先说明一下双阶乘就是隔项连乘,如

后面将采用Wallis积分的阶乘表示形式.(公式见上图)
由 1-x2 的形式,易想到令x=cost,但这里是 x-x2 可考虑升次令 x=cos2t,t∈[0,π/2]
然后凑微分变为单一变量(只含cosx 或 sinx)三角函数,过程如下
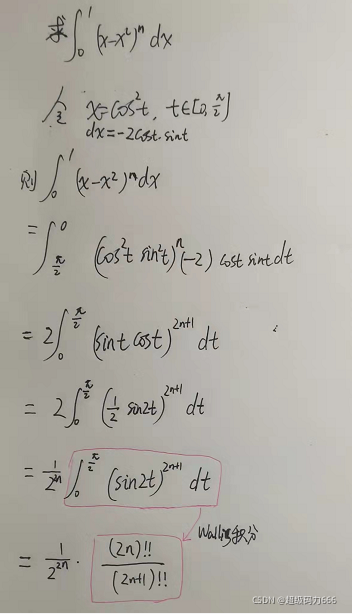
(2)公式化简(组合数学)
上面(1)中公式还可化简,要有点组合数学基础.
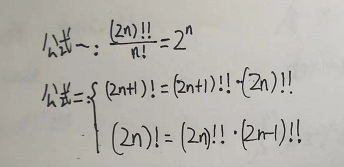
上图公式二是单阶乘与双阶乘的转换,容易推出
公式一需结合式子,模拟推算一下 (2n)!!与2的n次方的比例关系
结合上面公式,最终化简如下