[数据结构与算法]学习数据结构笔记(9) --- [二叉树学习(BinaryTree)]

B站学习传送门–>尚硅谷Java数据结构与java算法（Java数据结构与算法）

1.初步学习二叉树

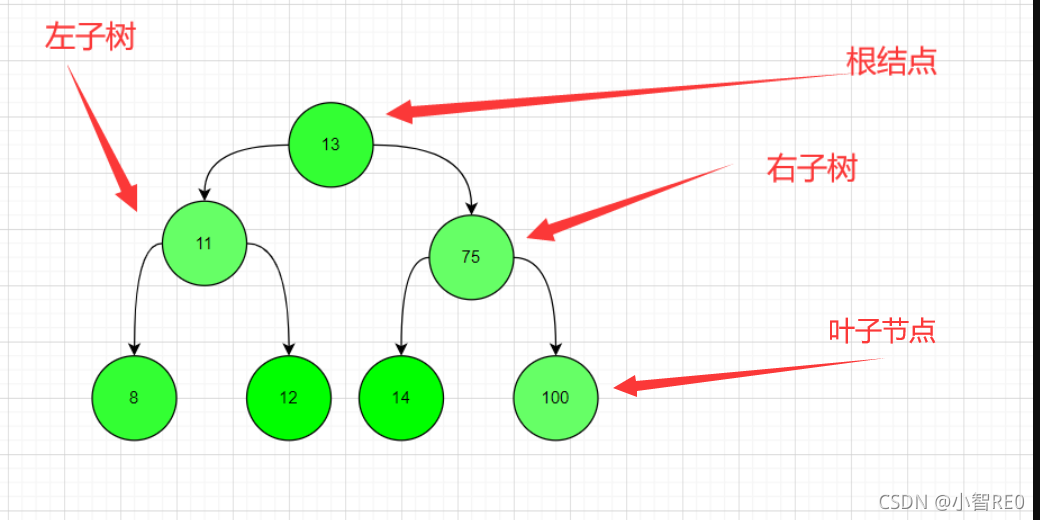
注意,从二叉树的基础开始

二叉树;在根节点的基础上;

• 根节点左边的节点一般称为左子树;
• 根节点右边的节点一般称为右子树;
• 每一部分单独取出都能看做一颗二叉树

满二叉树:所有的根结点都挂有左子树和右子树

2.初步实现二叉树的前序,中序,后序遍历

本次先手动创建二叉树; 主要是学习二叉树的前序,中序,后序遍历思想

图解

先对之前这个图进行分析;

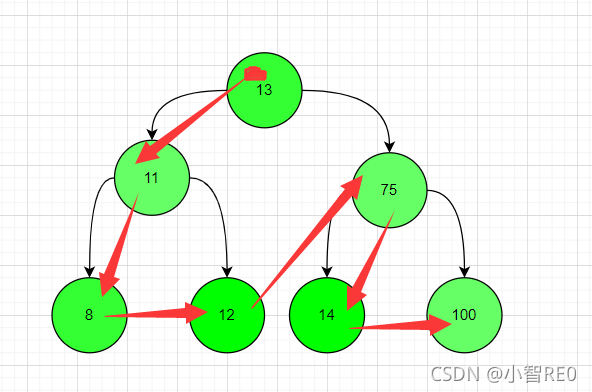
前序遍历:

获取输出顺序: 根结点(中间的节点) —> 左子树 —>右子树

例如:刚才创建的二叉树进行前序遍历的话;
就得输出 13 --> 11 --> 8 --> 12 --> 75 --> 14 --> 100

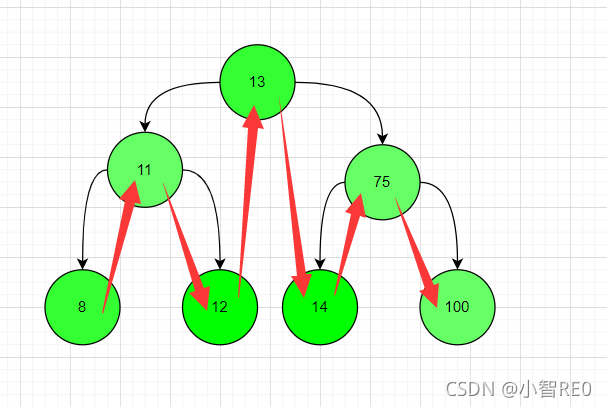
中序遍历:
获取输出顺序; 左子树 —> 中心节点 —> 右子树
例如刚才的二叉树进行中序遍历就是;
8 --> 11 --> 12 --> 13 --> 14 --> 75 --> 100

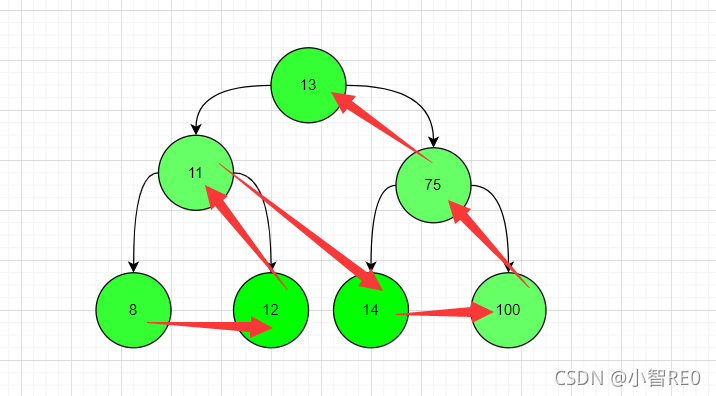
后序遍历;
输出顺序: 左子树 —> 右子树 —> 中心节点

刚才的二叉树输出顺序为;

8 --> 12 --> 11 --> 14 --> 100 --> 75 --> 13

简易实现前中后序遍历

/**
 * @author by CSDN@小智RE0
 * @date 2021-11-10 18:10
 */
public class DemoTree {
    public static void main(String[] args) {

        //手动创建二叉树;
        BinarTree  btree = new BinarTree();
        //先创建节点;
        Node root  = new Node(13);
        Node node1 = new Node(11);
        Node node2 = new Node(75);
        Node node3 = new Node(8);
        Node node4 = new Node(12);
        Node node5 = new Node(14);
        Node node6 = new Node(100);

       //手动挂接子节点;
        root.setLeft(node1);
        root.setRight(node2);
        node1.setLeft(node3);
        node1.setRight(node4);
        node2.setLeft(node5);
        node2.setRight(node6);
        btree.setRoot(root);

        System.out.println("简易的前序遍历---");
        btree.prefixList();
        System.out.println("简易的中序遍历---");
        btree.infixList();
        System.out.println("简易的后序遍历---");
        btree.suffixList();
    }
}


//二叉树;
class BinarTree {
    //根结点;
    public Node root;

    //设置根结点;
    public void setRoot(Node root) {
        this.root = root;
    }

    //前序遍历;
    public void prefixList() {
        if (root == null) {
            System.out.println("空树,不遍历");
        } else {
            this.root.prefixList();
        }
    }

    //中序遍历;
    public void infixList() {
        if (root == null) {
            System.out.println("空树,不遍历");
        } else {
            this.root.infixList();
        }
    }

    //后序遍历;
    public void suffixList() {
        if (root == null) {
            System.out.println("空树,不遍历");
        } else {
            this.root.suffixList();
        }
    }
}

//节点;
class Node {
    //节点的值;
    private int val;
    //左子树,右子树;
    private Node left;
    private Node right;

    public Node(int val) {
        this.val = val;
    }

    public int getVal() {
        return val;
    }

    public void setVal(int val) {
        this.val = val;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" + "val=" + val + '}';
    }

    //前序遍历;  中-->左-->右;
    public void prefixList() {
        //中心节点先输出;
        System.out.println(this);

        if (this.left != null) {
            //去左子树;
            this.left.prefixList();
        }

        if (this.right != null) {
            //去右子树;
            this.right.prefixList();
        }
    }

    //中序遍历;  左-->中-->右;
    public void infixList() {
        //先去左子树;
        if (this.left != null) {
            this.left.infixList();
        }
        //中心节点;
        System.out.println(this);
        //在去右子树;
        if (this.right != null) {
            this.right.infixList();
        }
    }

    //后序遍历;  左-->右-->中;
    public void suffixList() {
        //左子树;
        if (this.left != null) {
            this.left.suffixList();
        }
        //右子树;
        if (this.right != null) {
            this.right.suffixList();
        }
        //中心点输出
        System.out.println(this);
    }

}

测试结果;

简易的前序遍历---
Node{val=13}
Node{val=11}
Node{val=8}
Node{val=12}
Node{val=75}
Node{val=14}
Node{val=100}
简易的中序遍历---
Node{val=8}
Node{val=11}
Node{val=12}
Node{val=13}
Node{val=14}
Node{val=75}
Node{val=100}
简易的后序遍历---
Node{val=8}
Node{val=12}
Node{val=11}
Node{val=14}
Node{val=100}
Node{val=75}
Node{val=13}

3.初步实现二叉树的前序查找,中序查找;后序查找;

那么这个前序查找,中序查找,后序查找时,就得根据他这个遍历时的顺序一样;一步步查找即可;

前序查找

• 首先就判断当前的这个结点是否符合;
• 若当前结点不符合,就先判断左子树是否为空;若不为空则在左子树向下进行递归;
• 若在左子树递归后找到要查找的节点;就直接返回,
• 若没有在左子树下找到,就去判断右子树是否为空,不为空就去递归查找;
• 最终若还是没有找到,返回一个空节点.

中序查找

• 首先判断当前结点的左子树是否为空;不为空就进行递归;
• 若在左子树递归找到就直接返回;
• 判断当前结点是否符合;
• 再去判断当前结点的右子树是否为空,不为空就进行递归;
• 最终还未找到,返回一个空节点;

后序查找

• 首先判断当前结点的左子树是否为空,不为空就进行递归;
• 若在左子树递归找到就直接返回;
• 再去判断当前结点的右子树是否为空;不为空就进行递归;
• 若在右子树递归找到就直接返回;
• 判断当前结点是否符合;
• 最终还未找到,返回一个空节点.

/**
 * @author by CSDN@小智RE0
 */
public class DemoTree {
    public static void main(String[] args) {
        //手动创建二叉树;
        BinarTree btree = new BinarTree();
        //先创建节点;
        Node root = new Node(13);
        Node node1 = new Node(11);
        Node node2 = new Node(75);
        Node node3 = new Node(8);
        Node node4 = new Node(12);
        Node node5 = new Node(14);
        Node node6 = new Node(100);

        //手动挂接子节点;
        root.setLeft(node1);
        root.setRight(node2);
        node1.setLeft(node3);
        node1.setRight(node4);
        node2.setLeft(node5);
        node2.setRight(node6);
        btree.setRoot(root);

        System.out.println("前序查找测试--->");
        btree.prefixSearch(14);
        System.out.println("中序查找测试--->");
        btree.infixSearch(14);
        System.out.println("后序查找测试--->");
        btree.suffixSearch(14);
    }
}


//二叉树;
class BinarTree {
    //根结点;
    public Node root;

    //设置根结点;
    public void setRoot(Node root) {
        this.root = root;
    }

    //前序查找;
    public void prefixSearch(int val) {
        if (root == null) {
            System.out.println("空树,不用查找");
        } else {
            Node node = this.root.prefixSearch(val);
            if (node == null) {
                System.out.println("没有找到");
            } else {
                System.out.println("已找到节点" + node.getVal());
            }
        }
    }

    //中序查找;
    public void infixSearch(int val) {
        if (root == null) {
            System.out.println("空树,不用查找");
        } else {
            Node node = this.root.infixSearch(val);
            if (node == null) {
                System.out.println("没有找到");
            } else {
                System.out.println("已找到节点" + node.getVal());
            }
        }
    }

    //后序查找;
    public void suffixSearch(int val) {
        if (root == null) {
            System.out.println("空树,不用查找");
        } else {
            Node node = this.root.suffixSearch(val);
            if (node == null) {
                System.out.println("没有找到");
            } else {
                System.out.println("已找到节点" + node.getVal());
            }
        }
    }
}

//节点;
class Node {
    //节点的值;
    private int val;
    //左子树,右子树;
    private Node left;
    private Node right;

    public Node(int val) {
        this.val = val;
    }

    public int getVal() {
        return val;
    }

    public void setVal(int val) {
        this.val = val;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" + "val=" + val + '}';
    }

    //前序查找步骤;
    public Node prefixSearch(int val) {
        //前序遍历时, 中-->左-->右;
        System.out.println("正在前序查找中------>");
        //1.先判断当前结点是否为空;
        if (this.val == val) {
            return this;
        }
        Node resultNode = null;
        //若不符合,则先看左子树是否为null; 不为空则向左一直递归;
        if (this.left != null) {
            resultNode = this.left.prefixSearch(val);
        }
        //在左子树找到就提前返回;
        if (resultNode != null) {
            return resultNode;
        }
        //若左子树未找到则在右子树递归查找;
        //看右子树是否为空;
        if (this.right != null) {
            resultNode = this.right.prefixSearch(val);
        }
        //最终再返回这个查询的节点;若为null就是没找到;
        return resultNode;
    }

    //中序查找步骤;
    public Node infixSearch(int val) {
        //中序遍历时;左-->中-->右;
        Node resultNode = null;
        //先判断左子树是否为空;不为空再去查找;
        if (this.left != null) {
            resultNode = this.left.infixSearch(val);
        }
        //若已找到,就提前返回;
        if (resultNode != null) {
            return resultNode;
        }
        System.out.println("正在中序查找中------>");
        //判断当前节点是否符合;
        if (this.val == val) {
            return this;
        }
        //判断右子树是否为空,再去递归查找;
        if (this.right != null) {
            resultNode = this.right.infixSearch(val);
        }
        //最终返回结果节点;若为null则就是没找到;
        return resultNode;
    }

    //后序查找步骤;
    public Node suffixSearch(int val) {
        //后序遍历时,左-->右 -->中;
        Node resultNode = null;
        //同样地,先判断左子树是否为空;
        if (this.left != null) {
            resultNode = this.left.suffixSearch(val);
        }
        //若找到则提前返回;
        if (resultNode != null) {
            return resultNode;
        }
        //右子树递归;
        if (this.right != null) {
            resultNode = this.right.suffixSearch(val);
        }
        //若找到就提前返回;
        if (resultNode != null) {
            return resultNode;
        }
        System.out.println("正在后序查找中------>");
        //判断当前节点是否符合;
        if (this.val == val) {
            return this;
        }
        //最终再返回这个结果节点,若为null就是没找到;
        return resultNode;
    }

}

测试结果:

前序查找测试--->
正在前序查找中------>
正在前序查找中------>
正在前序查找中------>
正在前序查找中------>
正在前序查找中------>
正在前序查找中------>
已找到节点14
中序查找测试--->
正在中序查找中------>
正在中序查找中------>
正在中序查找中------>
正在中序查找中------>
正在中序查找中------>
已找到节点14
后序查找测试--->
正在后序查找中------>
正在后序查找中------>
正在后序查找中------>
正在后序查找中------>
已找到节点14

4. 初步实现二叉树的删除

• 具体实现时,先在当前结点的左边查找;若符合就删除,然后在当前结点的右边查找,若符合就删除;
• 然后还没找到的话,从当前结点的左子树向下递归, 直到递归到叶子节点;
• 从当前结点的右子树也向下递归,直达叶子节点;
• 实际上这里操作时的当前节点不是固定的一个节点;是一直变动的节点;它要向左或向右递归下去;

具体实现过程

package day09binarysearchtree.demo01_starttree;

/**
 * @author by CSDN@小智RE0
 * @date 2021-11-10 18:10
 */
public class DemoTree {
    public static void main(String[] args) {

        //手动创建二叉树;
        BinarTree btree = new BinarTree();
        //先创建节点;
        Node root = new Node(13);
        Node node1 = new Node(11);
        Node node2 = new Node(75);
        Node node3 = new Node(8);
        Node node4 = new Node(12);
        Node node5 = new Node(14);
        Node node6 = new Node(100);

        //手动挂接子节点;
        root.setLeft(node1);
        root.setRight(node2);
        node1.setLeft(node3);
        node1.setRight(node4);
        node2.setLeft(node5);
        node2.setRight(node6);
        btree.setRoot(root);
        System.out.println("简易的前序遍历---");
        btree.prefixList();
        //删除指定的节点;
        btree.deleteNode(8);
        System.out.println("删除了结点后简易的前序遍历---");
        btree.prefixList();
    }
}


//二叉树;
class BinarTree {
    //根结点;
    public Node root;
    //设置根结点;
    public void setRoot(Node root) {
        this.root = root;
    }

    //调用删除指定的元素;
    public void deleteNode(int val){
        //首先排除空树;
        if(root!=null){
            //在判断这个树的节点是否符合;
            if(root.getVal()==val){
                root =null;
            }else {
                root.deleteNode(val);
            }
        }else {
            System.out.println("空树,无法删除");
        }
    }


    //前序遍历;
    public void prefixList() {
        if (root == null) {
            System.out.println("空树,不遍历");
        } else {
            this.root.prefixList();
        }
    }
}

//节点;
class Node {
    //节点的值;
    private int val;
    //左子树,右子树;
    private Node left;
    private Node right;

    public Node(int val) {
        this.val = val;
    }

    public int getVal() {
        return val;
    }

    public void setVal(int val) {
        this.val = val;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" + "val=" + val + '}';
    }


    //删除二叉树中的节点;
    public void deleteNode(int val){
        //首先看左子树是否为空,若为空且符合,就删除;
        if(this.left!=null && this.left.val==val){
            this.left = null;
            return;
        }
        //然后去看右子树是否为空,若为空且符合,就删除;
        if(this.right!=null && this.right.val==val){
            this.right = null;
            return;
        }

        //然后在看左子树是否为空,进行递归;
        if (this.left!=null){
            this.left.deleteNode(val);
        }

        //向右递归;
        if (this.right!=null){
            this.right.deleteNode(val);
        }
    }

    //前序遍历;  中-->左-->右;
    public void prefixList() {
        //中心节点先输出;
        System.out.println(this);

        if (this.left != null) {
            //去左子树;
            this.left.prefixList();
        }

        if (this.right != null) {
            //去右子树;
            this.right.prefixList();
        }
    }
}

测试结果:

简易的前序遍历---
Node{val=13}
Node{val=11}
Node{val=8}
Node{val=12}
Node{val=75}
Node{val=14}
Node{val=100}
删除了结点后简易的前序遍历---
Node{val=13}
Node{val=11}
Node{val=12}
Node{val=75}
Node{val=14}
Node{val=100}

5.顺序存储二叉树(完成前中后序遍历)

由上至下,由左到右;对一个二叉树进行遍历;
遍历得到的数组, 可以和二叉树相互转换;或者说即使将这个二叉树变为数组,那么也能通过这个数据推导出前序/中序/后序遍历;

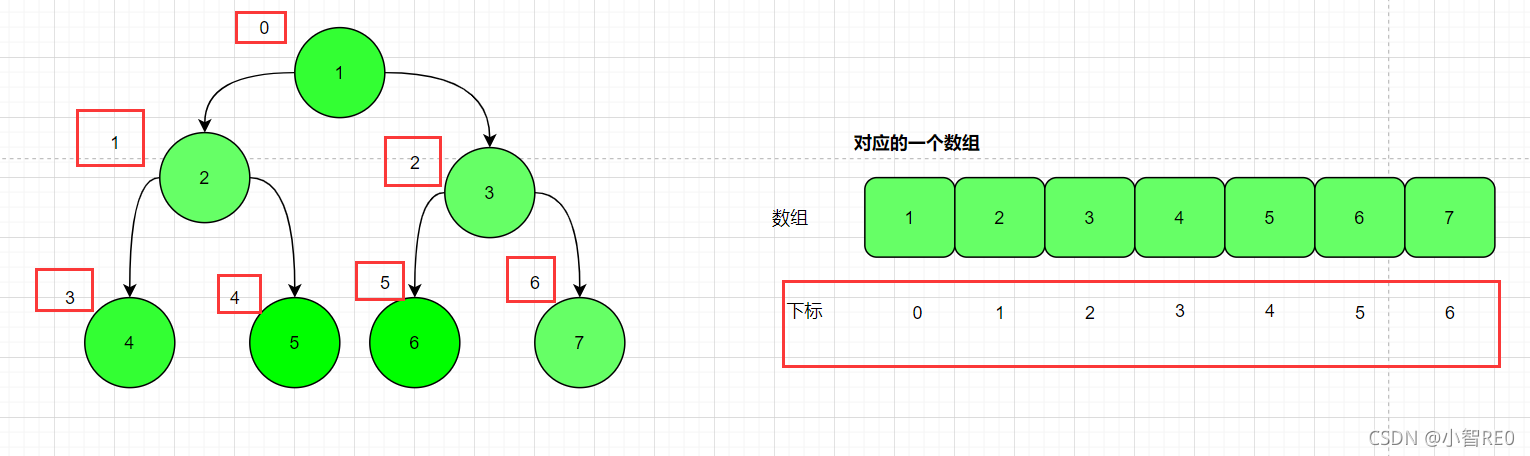
• 顺序存储二叉树的话,一般是对于完全二叉树来说的;
• 顺序存储时的二叉树,特点是,第N个元素(从零开始);的左子树节点为 2N+1; 第N个元素的右子树节点为2N+2;

具体实现顺序存储二叉树的前中后序遍历

package day09binarysearchtree.demo02_sequentialstorageofbinarytrees;

/**
 * @author by CSDN@小智RE0
 * @date 2021-11-11 18:50
 * 顺序存储二叉树
 */
public class SequentialStorageOfBinaryTreeTest {
    public static void main(String[] args) {
        //要进行存储的数组;
        int[] array = {1, 2, 3, 4, 5, 6, 7};
        SequentialStorageOfBinaryTree storage = new SequentialStorageOfBinaryTree(array);
        //前序遍历;
        storage.prefixList();
        //中序遍历;
        storage.infixList();
        //后序遍历;
        storage.suffixList();
        /*
        前序遍历-->1->2->4->5->3->6->7->
        中序遍历-->4->2->5->1->6->3->7->
        后序遍历-->4->5->2->6->7->3->1->
         */
    }
}

//模拟顺序存储二叉树;
class SequentialStorageOfBinaryTree {
    //用数组作为存储结构;
    private final int[] data;

    //初始化;
    public SequentialStorageOfBinaryTree(int[] data) {
        this.data = data;
    }

    //完成前序遍历;
    public void prefixList() {
        System.out.print("前序遍历-->");
        prefixList(0);
        //打印空行进行换行;
        System.out.println();
    }

    /**
     * 顺序存储二叉树的前序遍历
     * 中-> 左 -> 右
     * @param i 数组索引
     */
    private void prefixList(int i) {
        //先排除空树的状况;
        if (data == null || data.length == 0) {
            System.out.println("空树,无法遍历");
            return;
        }

        //进行遍历时,首先取到当前的节点;
        System.out.printf("%d->", data[i]);

        //向左递归/向右递归时,都要注意这个是否超出数组的长度;
        if ((2 * i) + 1 < data.length) {
            prefixList(2 * i + 1);
        }
        if ((2 * i + 2) < data.length) {
            prefixList(2 * i + 2);
        }
    }

    //完成中序遍历;
    public void infixList() {
        System.out.print("中序遍历-->");
        infixList(0);
        System.out.println();
    }

    /**
     * 顺序存储二叉树的中序遍历
     * 左 -> 中 -> 右
     * @param i 数组的下标
     */
    private void infixList(int i) {
        //先排除空树;
        if (data == null || data.length == 0) {
            System.out.println("空树,不需要遍历");
            return;
        }

        //先进行左递归;
        if ((2 * i) + 1 < data.length) {
            infixList((2 * i) + 1);
        }
        //再打印当前元素;
        System.out.printf("%d->", data[i]);
        //进行右递归;
        if ((2 * i + 2) < data.length) {
            infixList((2 * i) + 2);
        }
    }

    //完成后序遍历;
    public void suffixList() {
        System.out.print("后序遍历-->");
        suffixList(0);
        System.out.println();
    }

    /**
     * 顺序存储二叉树的后序遍历
     * 左 - > 右 -> 中
     * @param i 数组的下标
     */
    private void suffixList(int i) {
        //先排除空树;
        if (data == null || data.length == 0) {
            System.out.println("空树,不需要遍历");
            return;
        }

        //先向左递归;
        if ((2 * i) + 1 < data.length) {
            suffixList((2 * i) + 1);
        }
        //再向右递归;
        if ((2 * i) + 2 < data.length) {
            suffixList((2 * i) + 2);
        }
        //打印当前数组元素;
        System.out.printf("%d->", data[i]);
    }

}

6. 线索化二叉树

线索化二叉树;不是一个特定的树,
对二叉树的前序遍历进行优化;可得到前序线索化二叉树;
类似的有中序线索化二叉树;后序线索化二叉树;

比如说有这样一颗树;它的中序遍历输出可作为一个数列 8 -> 3 -> 10 -> 1 -> 14 -> 6

但是它有7个空指针域 ;会出现空间的浪费;
那么这时就得需要为它添加前驱指针(指向前一个结点);后继指针(指向后一个结点);

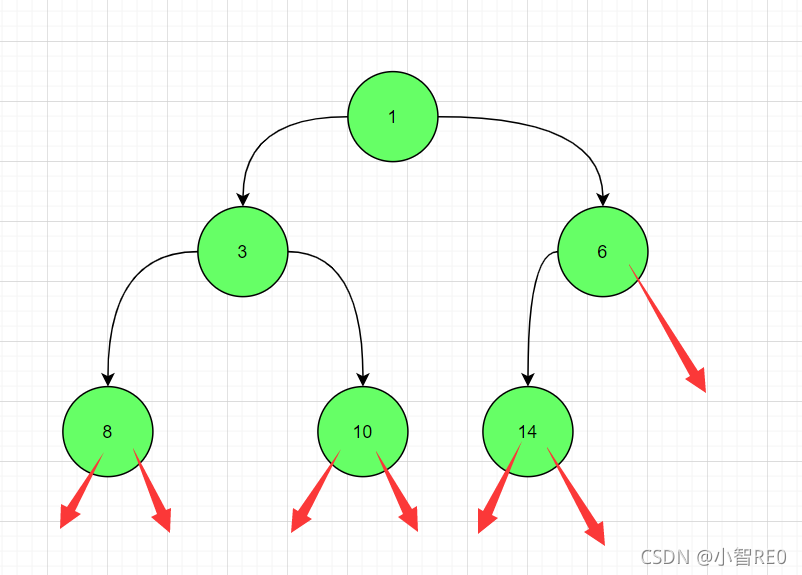
那么,这时,若要用前驱节点/后继节点补齐这个二叉树的话;
大概完成为下图;

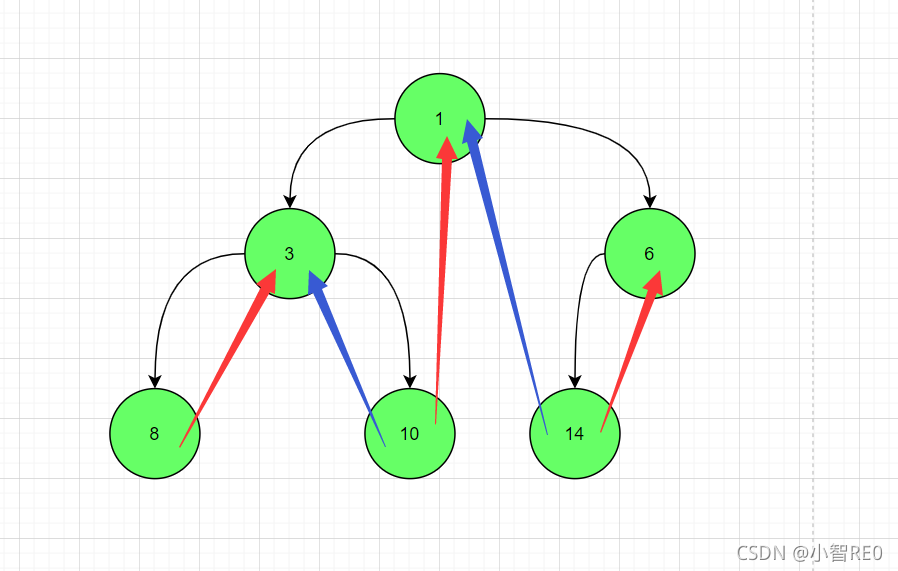
可以注意到的是,有时候树中这个指向为left的指针可能会指向左子树,也会指向前驱节点;
树中指向为right的指针可能会指向右子树,也会指向后继节点;
那么实现时,可以用两个变量来区分一下(前驱指针/左子树); (后驱指针/右子树)

那么在具体实现中序搜索化时,需要注意的时,可以指定一个变量作为前驱节点即可,存放上一个节点;
然后,上次的操作节点的后继节点就是当前操作的节点;

还有,当前的二叉树在经过搜索化时,由于多了指针,这样的话,原有的结构被打乱;若还使用之前的输出遍历方式,会出现空指针异常问题;
那么就需要对应的重新编排遍历的方法;
而且,需要注意的是,在经过前序搜索化的二叉树,就应该对应地进行前序遍历输出打印;
经历中序搜索化的二叉树,对应进行中序遍历输出打印;
经历后序搜索化的二叉树,对应进行后序遍历输出打印;

package day09abouttree.demo03_linearbinarytree;

/**
 * @author by CSDN@小智RE0
 * @date 2021-11-11 19:25
 * 线索化二叉树的使用
 */
public class LinearBinaryTreeTest {
    //测试;
    public static void main(String[] args) {
        ClueTree clueTree = new ClueTree();
        Node root = new Node(1);
        Node node1 = new Node(8);
        Node node2 = new Node(3);
        Node node3 = new Node(10);
        Node node4 = new Node(14);
        Node node5 = new Node(6);
        //手动挂接节点;
        root.setLeft(node2);
        root.setRight(node5);
        node2.setLeft(node1);
        node2.setRight(node3);
        node5.setLeft(node4);
        clueTree.setRoot(root);

        //测试中序线索化二叉树;
        clueTree.preClueList();

        //测试值为 8 的节点的前驱与后继节点;
        Node left = node1.getLeft();
        Node right = node1.getRight();
        System.out.println("8号节点的前驱节点为->" + left);
        System.out.println("8号节点的后继节点为->" + right);

        System.out.println("-----对搜索化后的二叉树进行中序遍历--------");
        //进行中序遍历;
        clueTree.prefixList();
    }
}


//二叉树;
class ClueTree {
    //根结点;
    public Node root;

    //设置根结点;
    public void setRoot(Node root) {
        this.root = root;
    }

    //----------------------------------------------->

    //定义前驱结点;
    public Node preNode = null;


    public void preClueList() {
        preClueList(root);
    }

    //中序线索化二叉树;
    private void preClueList(Node node) {
        //首先排除空树;
        if (node == null) {
            return;
        }

        //进行左递归;
        preClueList(node.getLeft());

        //处理当前结点时;
        //1.首先是前驱节点;
        // 这时要保证这个当前结点的左子树为空时才能为它添加前驱节点;
        if (node.getLeft() == null) {
            //为它设置前驱节点;
            node.setLeft(preNode);
            //改变这个指针的类型;
            node.setPreType(1);
        }

        //2.后继节点的处理;
        //同样地,保证这个结点的右子树为空时才给它添加后继节点;
        //需要明白的一点时,这个点的前驱节点实际上就是上一个操作的节点;
        if (preNode != null && preNode.getRight() == null) {
            //为它设置节点;
            preNode.setRight(node);
            //改变指针的类型;
            preNode.setSuffixType(1);

        }
        //3.这时需要让当前结点作为前置节点;
        preNode = node;

        //右递归
        preClueList(node.getRight());
    }

    //----------------------------------------------->

    //中序遍历输出二叉树;
    public void prefixList() {
        //将根结点存为操作节点;
        Node temp = root;

        while (temp != null) {
            //先找前驱节点;
            while (temp.getPreType() == 0) {
                //向左查找;
                temp = temp.getLeft();
            }
            //输出当前结点;
            System.out.println(temp);

            //若找到了后继节点;
            while (temp.getSuffixType() == 1) {
                //向右查找;
                temp = temp.getRight();
                //输出当前结点;
                System.out.println(temp);
            }
            //没找到,继续向右
            temp = temp.getRight();
        }
    }


}

//节点;
class Node {
    //节点的值;
    private int val;
    //左子树,右子树;
    private Node left;
    private Node right;

    //需要使用一个标记点;标记是左子树(0)/前驱结点(1)
    private int preType;
    //右子树(0) / 后继节点(1);
    private int suffixType;

    public int getPreType() {
        return preType;
    }

    public void setPreType(int preType) {
        this.preType = preType;
    }

    public int getSuffixType() {
        return suffixType;
    }

    public void setSuffixType(int suffixType) {
        this.suffixType = suffixType;
    }

    public Node(int val) {
        this.val = val;
    }

    public int getVal() {
        return val;
    }

    public void setVal(int val) {
        this.val = val;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" + "val=" + val + '}';
    }
}

测试实现

8号节点的前驱节点为->null
8号节点的后继节点为->Node{val=3}
-----对搜索化后的二叉树进行中序遍历--------
Node{val=8}
Node{val=3}
Node{val=10}
Node{val=1}
Node{val=14}
Node{val=6}