一、求二叉树的最近公共祖先
1.题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
2.输入输出示例
示例 1:
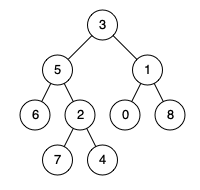
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例2:
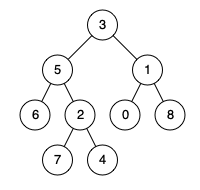
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:

二、思路分析
像这道题目,如果出现在笔试题中,有思路直接开始做就可以,但是如果出现在面试当中,切记一定要和面试官一起讨论:
1.如果树是采用双亲表示法或者孩子双亲表示法: 这时候其每一个结点中都含有对其双亲的引用,求最近公共祖先的问题就可以直接转化为两个链表相交求交点。
2.如果树是二叉搜索树结构: 关于二叉搜索树前面还没有提到过,后面会详细讲解,这里先简单列举一个二叉搜索树:

由题目给出的输入输出用例分析可得:
1.x== root||y ==root:最近公共祖先一定是根
2.x.data<root.data&&y.data>root.data:x和y刚好处于根的左右子树中,x和y的公共祖先一定是root
3.x.data<root.data&&y.data<root.data:x和y都存在于根的左子树中,递归到根的左子树中找x和y的最近公共祖先
4.x.data>root.data&&y.data>root.data:x和y都存在于根的右子树中,递归到根的右子树中找x和y的最近公共祖先
3.只是普通的二叉树: 下面来详细展开讲解
三、普通二叉树借鉴双亲表示法思想
情况一(也就是双亲表示法)相当于已经知道了两个结点的路径中包含了哪些结点
于是我们可以借鉴情况一这种方式:
如果能够知道从根结点到某个结点的路径中总共包含哪些结点即可
保存路径中结点的结构选择使用栈
因为当路径中包含的结点找到之后,需要从下往上比较才能找到最近的公共祖先
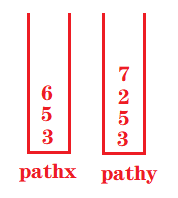
假设两个结点分别为6和7,栈中如下图所示:
那么如何求:一个结点路径中所包含的所有结点呢?代码如下:
boolean getNodePath(TreeNode root,Stack<TreeNode> s,TreeNode node){
if(root==null||node==null){
return false;
}
s.push(root);
if(root==node){
return true;
}
if(getNodePath(root.left,s,node)){
return true;
}
if(getNodePath(root.right,s,node)){
return true;
}
s.pop();
return false;
}
将结点全部保存至栈当中,记录两个栈的大小
比较栈顶元素相等不相等
当元素不相等时,比较两个栈的大小大小不一样时:将大的栈顶元素移除同时size–
大小一样时:将两者同时移除,并且同时对size–
主方法:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null||p==null||q==null){
return null;
}
//找从root到p或者q对应路径中包含的所有结点
Stack<TreeNode> pPath=new Stack<>();
Stack<TreeNode> qPath=new Stack<>();
getNodePath(root,pPath,p);
getNodePath(root,qPath,q);
int pSize=pPath.size();
int qSize=qPath.size();
while(!pPath.empty()&&!qPath.empty()){
if(pPath.peek()==qPath.peek()){
return pPath.peek();
}
if(pSize>qSize){
pPath.pop();
pSize--;
}else if(pSize<qSize){
qPath.pop();
qSize--;
}else{
pPath.pop();
qPath.pop();
pSize--;
qSize--;
}
}
return null;
}
}
四、普通二叉树借鉴二叉搜索树思想
在二叉搜索树中,我们可以知道结点的顺序,直接通过比较大小就可以判断结点在左子树还是右子树当中。
从这里受到启发,如果可以知道一个结点在其子树中的位置,也可以解决此问题:
//如果知道一个结点在其子树中的位置,也可以解决---想法来源于二叉搜索树
boolean isNodeInTree(TreeNode root,TreeNode node){
if(root==null||node==null){
return false;
}
if(root==node){
return true;
}
if(isNodeInTree(root.left,node)){
return true;
}
return isNodeInTree(root.right,node);
}
主方法:
这里采用四个布尔类型的数据来记录结点所在的位置
主要思想参照文章前面写的二叉搜索树
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return null;
}
//p和p只要有一个在根节点的位置,则最近公共祖先就是根节点
if(root==p||root==q){
return root;
}
boolean ispInLeft=false;
boolean ispInRight=false;
boolean isqInLeft=false;
boolean isqInRight=false;
//检测p是否在root的左子树中
if(isNodeInTree(root.left,p)){
ispInLeft=true;
ispInRight=false;
}else{
ispInLeft=false;
ispInRight=true;
}
//检测q是否在root的左子树中
if(isNodeInTree(root.left,q)){
isqInLeft=true;
isqInRight=false;
}else{
isqInLeft=false;
isqInRight=true;
}
if(ispInLeft&&isqInLeft){
return lowestCommonAncestor(root.left,p,q);
}else if(ispInRight&&isqInRight){
return lowestCommonAncestor(root.right,p,q);
}else{
return root;
}
}
}