21天零基础入门ACM

21天零基础入门ACM之第17天

gcd和exgcd

gcd

gcd 就是最大公因数的简称。
求最大公因数，常用的方法是辗转相除法。

辗转相除法，又名欧几里德算法（Euclidean
algorithm），是求最大公约数的一种方法。它的具体做法是：用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。

再c++中有一个库函数，__gcd(x,y),就是求x，y的最大公约数的。

inline ll gcd(ll x, ll y) { 
	return y ? gcd(y, x % y) : x; 
}

exgcd

exgcd，又叫拓展欧几里德，用来求形如 gcd(a,b)=ax+by 的方程的通解。
算法代码：

void exgcd(int &x,int &y,int a,int b)
{
    if(!b)
    {
        x=1;
        y=0;
        return;
    }
    exgcd(x,y,b,a%b);
    int t=x;
    x=y;
    y=t-a/b*y;
}

例题：

例题1：https://ac.nowcoder.com/acm/problem/14503
在这里插入图片描述

代码：

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1;    while (b) { if (b & 1)    ans *= a;        b >>= 1;        a *= a; }    return ans; }    
ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
inline ll read() { ll s = 0, w = 1; char ch = getchar(); while (ch < 48 || ch > 57) { if (ch == '-') w = -1; ch = getchar(); }    while (ch >= 48 && ch <= 57) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();    return s * w; }

const int mod=1e9+7;
const int N=1e5+7;

ll n,m,a,b,p;
int main(){
	while(cin>>n>>m>>p){
		ll ans=m*n/gcd(m,n);
        ans=ans*p/gcd(ans,p);
        cout<<ans<<endl;
	}
	return 0;
}

例题2：https://ac.nowcoder.com/acm/problem/15425
在这里插入图片描述

代码：

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1;    while (b) { if (b & 1)    ans *= a;        b >>= 1;        a *= a; }    return ans; }    
ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
inline ll read() { ll s = 0, w = 1; char ch = getchar(); while (ch < 48 || ch > 57) { if (ch == '-') w = -1; ch = getchar(); }    while (ch >= 48 && ch <= 57) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();    return s * w; }

const int mod=1e9+7;
const int N=1e5+7;

ll n,m,a,b,p;
int main(){
	while(cin>>n>>m){
		p=gcd(n,m);
        cout<<p<<" "<<n/p*m<<endl;
	}
	return 0;
}

例题3：https://ac.nowcoder.com/acm/problem/50565
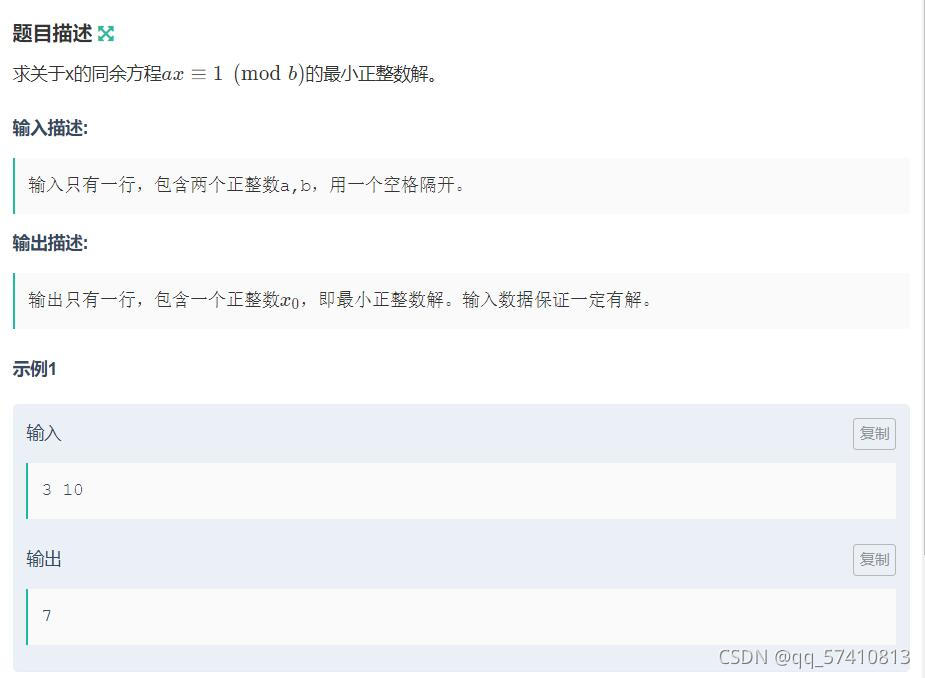
在这里插入图片描述
代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0){
        x=1;
        y=0;
        return a;
    }
    ll ans=exgcd(b,a%b,x,y);
   int t=x;
    x=y;
    y=t-a/b*y;
    return ans;
}

ll a,b,x,y;
signed main(){
    while(cin>>a>>b){
        int t=exgcd(a,b,x,y);
        b/=t;
        cout<<(x%b+b)%b<<endl;
    }
    return 0;
}
/*
t为常数
x的解集为 x+b/gcd()*t；
y的解集为 y-a/gcd()*t；
*/